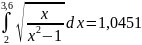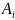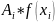1.2 Квадратурная формула трапеций
Разбиение отрезка [2; 3,6] на n=16 частей с шагом h=0,1
i |
|
|
Веса
|
|
|
|
0 |
2 |
0,816497 |
1,000000 |
0,816497 |
|
|
1 |
2,1 |
0,784752 |
2,000000 |
1,569504 |
|
|
2 |
2,2 |
0,756913 |
2,000000 |
1,513825 |
|
|
3 |
2,3 |
0,732209 |
2,000000 |
1,464419 |
|
|
4 |
2,4 |
0,710072 |
2,000000 |
1,420143 |
|
|
5 |
2,5 |
0,690066 |
2,000000 |
1,380131 |
|
|
6 |
2,6 |
0,671855 |
2,000000 |
1,343710 |
|
|
7 |
2,7 |
0,655174 |
2,000000 |
1,310348 |
|
|
8 |
2,8 |
0,639810 |
2,000000 |
1,279620 |
|
|
9 |
2,9 |
0,625590 |
2,000000 |
1,251180 |
|
|
10 |
3 |
0,612372 |
2,000000 |
1,224745 |
|
|
11 |
3,1 |
0,600039 |
2,000000 |
1,200077 |
|
|
12 |
3,2 |
0,588490 |
2,000000 |
1,176980 |
|
|
13 |
3,3 |
0,577642 |
2,000000 |
1,155284 |
|
|
14 |
3,4 |
0,567424 |
2,000000 |
1,134847 |
|
|
15 |
3,5 |
0,557773 |
2,000000 |
1,115547 |
|
|
16 |
3,6 |
0,548638 |
1,000000 |
0,548638 |
|
|
|
|
|
|
|
|
|
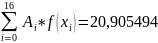
По формуле трапеций находим приближенное значение интеграла:

Разбиение
отрезка [2; 3,6] на
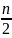 =
8 частей с шагом 2h=0,2
=
8 частей с шагом 2h=0,2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

По формуле трапеций находим приближенное значение интеграла:
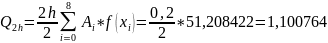
Вычислим
значение: k=
=
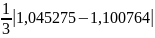 =0,0184964
=0,0184964
Так,
как полученное значение k>0,0001,
то продолжаем разбиение до n=32
с шагом
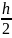 =
0,05
=
0,05
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
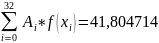
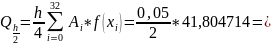 1,045118
1,045118
Вычислим
значение: k=
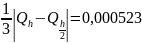
Так
как полученное значение k<0,0001,
то заданная точность удовлетворяет
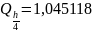 .
.
Округляем
значение
интеграла до трех знаков после запятой,
согласно точности вычислений 0,0001, и
получаем ответ: