
- •Курсовая работа по дисциплине «Теория электрической связи» «Расчёт основных характеристик системы передачи мультимедийной информации»
- •1. Цель курсовой работы
- •2. Содержание задания
- •3.Исходные данные
- •4. Модель системы передачи информации
- •5. Расчет основных характеристик сигнала
- •6. Спектр сигналов при фм
- •7. Определение корреляционной функции случайного телеграфного сигнала
- •8. Определение спектральной плотности мощности случайного телеграфного сигнала
- •9. Расчет спектральной плотности мощности сигнала при фм-4
- •10. Расчет помехоустойчивости при фм-4
- •11. Модулятор
- •12. Оптимальный демодулятор
- •13. Сверточный кодер
- •14. Перемежитель (деперемежитель)
5. Расчет основных характеристик сигнала
- полоса пропускания;
N=10 - количество поднесущих OFDM–сигнала;
Nп=3- количество пилот-сигналов;
r= 2/3 - относительная скорость кода;
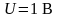 -
напряжение сигнала;
-
напряжение сигнала;
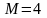 -
объем ансамбля сигнала;
-
объем ансамбля сигнала;
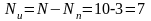 -
количество информационных сигналов;
-
количество информационных сигналов;
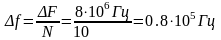 -
полоса частот элемента сигнала;
-
полоса частот элемента сигнала;
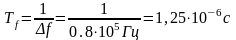 -
длительность посылки символа;
-
длительность посылки символа;
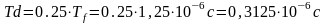 -
длительность защитного интервала;
-
длительность защитного интервала;
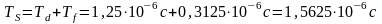 -
общее время посылки сигнала;
-
общее время посылки сигнала;
![]() -
количество кодированных двоичных
символов передачи на одной поднесущей;
-
количество кодированных двоичных
символов передачи на одной поднесущей;
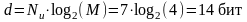 -
емкость OFDM-символа;
-
емкость OFDM-символа;
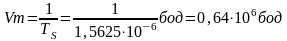 -
скорость телеграфирования на поднесущей;
-
скорость телеграфирования на поднесущей;
 -
скорость передачи информации на
поднесущей;
-
скорость передачи информации на
поднесущей;
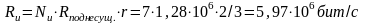 -
общая скорость передачи информации;
-
общая скорость передачи информации;
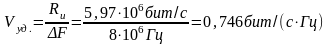 -
удельная скорость передачи информации.
-
удельная скорость передачи информации.
6. Спектр сигналов при фм
Технология OFDM
предусматривает, что информация
передается по многим поднесущим частотам,
образующим канал. OFDM – символ
представляет собой совокупность всех
поднесущих на дискретном временном
интервале. Суммарный сигнал на всех
поднесущих можно записать так:
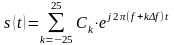 ,
где
,
где
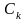 - комплексная амплитуда к-ой поднесущей.
- комплексная амплитуда к-ой поднесущей.
Сигнал на одной
поднесущей при фазовой модуляции ФМ-4
выражается формулой:
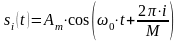 ,
где
,
где
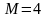 - градация сигнала,
- градация сигнала,
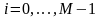 ,
,
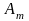 - максимальная амплитуда сигнала.
Поскольку максимальная амплитуда в
- максимальная амплитуда сигнала.
Поскольку максимальная амплитуда в
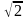 раз
больше среднеквадратического значения,
можно записать:
раз
больше среднеквадратического значения,
можно записать:
 .
При этом
.
При этом
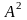 - это средняя мощность сигнала,
нормированная на 1 Ом,
поэтому:
- это средняя мощность сигнала,
нормированная на 1 Ом,
поэтому:
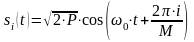 .
Воспользовавшись определением мощности:
.
Воспользовавшись определением мощности:
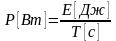 ,
получим:
,
получим:
 .
.
 - энергия сигнала. Полученное выражение
можно разложить по формуле косинуса
суммы:
- энергия сигнала. Полученное выражение
можно разложить по формуле косинуса
суммы:
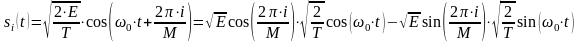 .
.
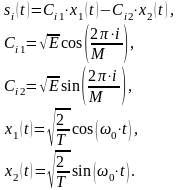
Выражение
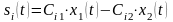 представляет собой линейную комбинацию
ортонормированных векторов (сигналов)
представляет собой линейную комбинацию
ортонормированных векторов (сигналов)
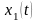 и
и
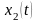 ,
то есть разложение по координатному
базису.
,
то есть разложение по координатному
базису.
Можно показать, что данная линейна комбинация векторов независимая
Найдем определитель Вронского:
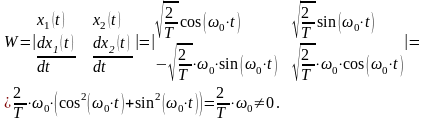
Так как определитель Вронского не равен нулю, то система ортонормированных векторов линейно независимая.
Сигнальное созвездие
при модуляции ФМ-4 представлено на рис.
3. Минимальные расстояния между соседними
точками сигнального созвездия одинаковы
и равны
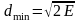 .
.
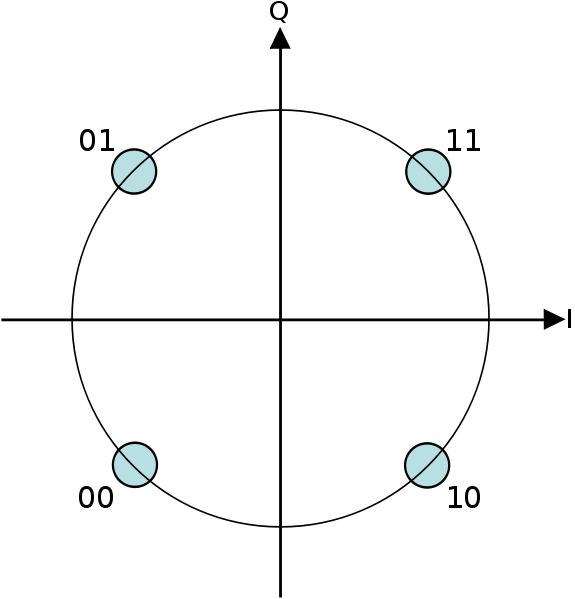
Рис. 3 Сигнальное созвездие при ФМ-4.
7. Определение корреляционной функции случайного телеграфного сигнала
сигнал телеграфный модулятор кодер перемежитель
Случайный телеграфный сигнал (СТС) представляет собой стационарный дискретный случайный процесс, принимающий на тактовых интервалах длительностью T значения +h с вероятностью p или –h с вероятностью 1-p. Вероятность принятия любого значения X(t) на к-ом тактовом интервале не зависит от того, какие значения он принял на (к-1)-ом тактовом интервале.
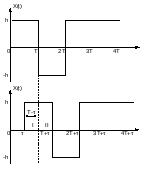
Рис 4. Случайный телеграфный сигнал.
Рассмотрим два
сечения СТС в моменты времени
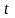 и
и
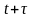 (рис. 4.).
Вычислим корреляционную функцию исходя
из ее определения:
(рис. 4.).
Вычислим корреляционную функцию исходя
из ее определения:
 .
Если
.
Если
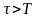 сечения принадлежат разным тактовым
интервалам, следовательно математическое
ожидание равно нулю (X(t)
и X(t+τ)
равновероятно принимают значения +h
и -h).
Поэтому корреляционная функция также
равна нулю. Если
сечения принадлежат разным тактовым
интервалам, следовательно математическое
ожидание равно нулю (X(t)
и X(t+τ)
равновероятно принимают значения +h
и -h).
Поэтому корреляционная функция также
равна нулю. Если
 ,
то математическое ожидание
,
то математическое ожидание
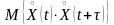 равно вероятности того, что оба сечения
находятся в одном интервале. Учитывая
свойство четности корреляционной
функции и то, что
равно вероятности того, что оба сечения
находятся в одном интервале. Учитывая
свойство четности корреляционной
функции и то, что
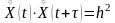 ,
получим:
,
получим:
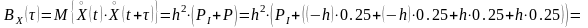
 .
.
При
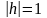 ,
получим:
,
получим:
 .
.
Таким образом,
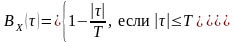
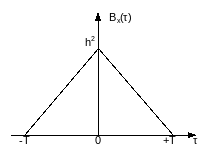 h2=1
h2=1
Рис. 5. Корреляционная функция случайного телеграфного сигнала.
