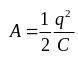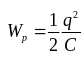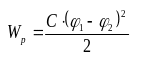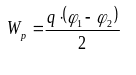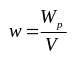- •Плоский конденсатор
- •Напряженность электростатического поля плоского конденсатора.
- •Электроемкость плоского конденсатора.
- •Параллельное соединение конденсаторов.
- •Смешанное соединение конденсаторов
- •Зарядить конденсатор – это значит
- •Энергия заряженного конденсатора.
- •Движение заряженной частицы в электростатическом поле.
Зарядить конденсатор – это значит
произвести разделение зарядов на его обкладках. Это можно сделать за счёт работы внешних сил. В результате такой работы, согласно закону сохранения энергии, заряженные обкладки приобретают потенциальную энергию.
Энергия заряженного конденсатора.
Заряженный конденсатор обладает энергией, возникающей в процессе зарядки конденсатора. Это потенциальная энергия взаимодействия разноименно заряженных обкладок конденсатора. Если одну из пластин плоского конденсатора предоставить саму себе, то она под действием силы поля второй пластины будет к ней притягиваться, увеличивая скорость и, как следствие, свою кинетическую энергию. В момент соприкосновения пластин конденсатора вся потенциальная энергия перейдет в кинетическую, а после – во внутреннюю, нагревая пластины. Первая пластина конденсатора, в таком случае, приближается ко второй за счет работы, которую совершает поле второй пластины.
Выразим величину силы, с которой электрическое поле второй пластины притягивает к себе первую (при этом будем считать, что вторая пластина конденсатора заряжена отрицательно, а первая – положительно).
Из
определения напряженности электростатического
поля следует, что:
![]() .
.
Избавляясь
от векторов, получим:
![]() .
.
![]() – это
напряженность поля второй пластины.
– это
напряженность поля второй пластины.
Для
заряженной бесконечной плоскости
![]() .
.
Здесь
![]() – поверхностная плотность заряда второй
пластины.
– поверхностная плотность заряда второй
пластины.
Тогда
![]() ,
а
,
а
![]()
Учитывая, что заряды обеих пластин конденсатора одинаковые, и их абсолютные значения называются зарядом конденсатора
(![]() где
где
![]() –
это заряд конденсатора), то
–
это заряд конденсатора), то
![]()
Вычислим работу постоянной силы, с которой поле второй пластины конденсатора притягивает к себе первую пластину:
 .
.
Учитывая,
что электроемкость плоского конденсатора
выражается по формуле
![]() ,
получаем:
,
получаем:
|
Также работа равна убыли потенциальной энергии:
![]()
Так
как кинетическая энергия первой пластины
принимает свое максимальное значение
в момент соприкосновения пластин, то
потенциальную энергию взаимодействия
пластин в этот момент времени можно
считать равной нулю
![]() .
.
Тогда
|
|
|
Используя определение электроемкости конденсатора,
|
|
или |
|
Энергия электрического поля.
Работу по переносу первой пластины можно выразить также через напряженность электростатического поля конденсатора.
![]() ,
,
где – это напряженность поля второй пластины.
Электростатическое поле конденсатора почти полностью сосредоточено между его пластинами, и
![]() ,
а так как
,
а так как
![]() ,
следовательно
,
следовательно
![]() ,
или
,
или
![]() .
.
Учтем
также, что из выражения
![]() следует, что
следует, что
![]()
Тогда выражение для работы принимает вид:
![]()
Так
как для нашего случая
![]() ,
то
,
то
![]()
Потенциальная энергия электростатического поля пропорциональна квадрату величины напряженности электростатического поля и величине объема, в котором локализовано это поле. |
|
Объемная плотность энергии электростатического поля.
Физическая величина, равная величине потенциальной энергии электростатического поля, локализованного в единице объема. |
|
В системе СИ объемная плотность энергии электростатического поля выражается: |
|
Используя
выражение для потенциальной энергии
поля в конденсаторе, получим:
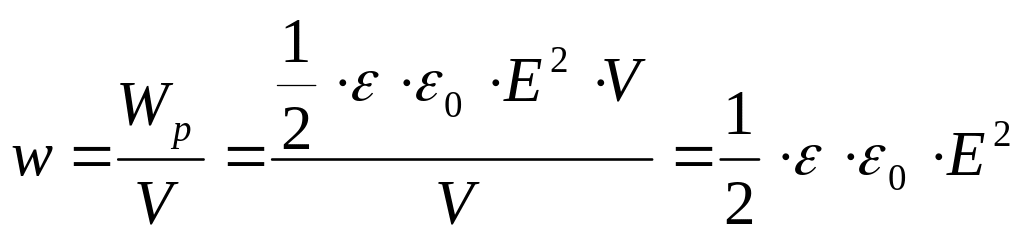
Объемная плотность энергии электростатического поля пропорциональна квадрату напряженности поля. |
|
Полученная формула справедлива не только для однородного поля, но и для любого другого электрического поля.