Температурная стабильность кпе.

Ёмкость любого конденсатора можно представить в виде двух составляющих:

- постоянная часть, её величина не зависит от положения ротора;

- переменная часть, которая изменяется при настройке.

Тогда результирующее значение ТКЕ КПЕ, К^-1:

Температурный коэффициент постоянной части, К^-1:

,

где , - ТКЕ конденсатора через воздух и твёрдый диэлектрик соответственно.

измеряется в основном ТК диэлектрической проницаемости изолятора .

ТКЕ конденсатора через твёрдый диэлектрик, К^-1:

- ТК диэлектрической проницаемости изолятора.

ТКЕ конденсатора через воздух:

- ТК диэлектрической проницаемости воздуха, К^-1.

- ТК материала пластин, К^-1.

- ТК зазора между кромками ротора и статора, К^-1.

m = 2 мм , h = 1 мм

Тогда:

Температурный коэффициент переменной части , К^-1:

- ТК зазора, К^-1.

- зазор между пластинами одного знака, мм.

Тогда

Тогда результирующее значение ТКЕ КПЕ, К^-1:

2. Катушка индуктивности

Катушка индуктивности представляет собой конструкцию, в которой на каркасе из диэлектрика размещено определённое количество витков провода.

Индуктивность контура 85.4 мкГн.

Т огда величина индуктивности колебательного контура будет равна:

Диаметр каркаса катушки индуктивности .

Расчёт числа витков катушки индуктивности. Число витков на единицу длины:

,

d – диаметр провода без изоляции, мм.

d = 0.55 мм. Изоляция для провода ПЭВ-1, эмалированная, диаметр – 0.05 мм.

Диаметр провода в изоляции d₀ = 0.55 + 0.05 = 0.6 мм.

Коэффициент неплотности намотки =1.3.

витков/см

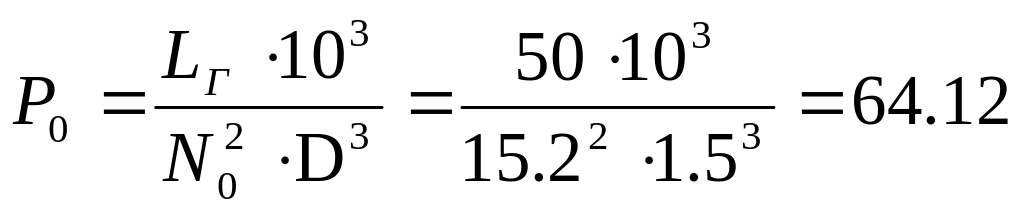
Отношение l/D=8. Длина намотки, см:

Тогда число витков:

Проверим величину индуктивности:

,

Здесь:

- коэффициент, зависящий от значения l/D;

N – число витков;

D – диаметр каркаса, см.

L₀ = 1.2

Тогда:

Полученное значение индуктивности отличается от ранее рассчитанного на 5%, следовательно, расчёт катушки индуктивности сделан верно.

Оптимизация длины провода

Обеспечение максимальной добротности катушки достигается оптимизацией диаметра провода.

Сначала вычислим вспомогательный коэффициент:

Здесь = 1.97 МГц

Вспомогательный параметр:

Здесь:

N – число витков;

D – диаметр катушки, см.

K = 3 – поправочный коэффициент, определяемый по графикам зав-ти от l/D.

Оптимальный диаметр провода, мм:

мм.

Изоляция провода – ПЭВ-I, .

Расчёт сопротивления провода катушки.

Активное сопротивление катушки, от которого зависит её добротность, складывается из сопротивления провода току высокой частоты и сопротивлений, вносимых диэлектрическими потерями в каркасе и собственной ёмкостью катушки индуктивности, потерями в экранах и сердечниках и т. п.

Полное активное сопротивление току высокой частоты равно:

Здесь: d – диаметр провода без изоляции, см;

D – диаметр однослойной катушки, см;

K – коэффициент, учитывающий влияние размеров катушки на эффект близости.

d = 0.041 см, D = 1.5 см, K = 3, N = 153.6

Значение коэффициентов F(z) и G(z) выражаются через функции Бесселя.

,

где d – диаметр провода, см,

f – средняя частота, Гц.

Сопротивление провода постоянному току, Ом:

Здесь: - удельное сопротивление провода, ;

d₀ – диаметр провода без изоляции, мм;

D – диаметр катушки индуктивности, м.

Провод медный, .

D = 0.015 м

Тогда полное активное сопротивление току высокой частоты , Ом:

Ом.

Вычислим собственную ёмкость катушки индуктивности. Собственная ёмкость катушки индуктивности С₀ образуется из ёмкостей между витками катушки и соседними металлическими деталями и является распределённой по всей длине катушки.

Д ля однослойной катушки:

Здесь k – коэффициент, величина которого зависит от соотношений между шагом намотки и диаметром провода;

τ = d_из = 0.04 мм - шаг намотки;

k₁ - коэффициент, величина которого зависит от соотношений между длиной и диаметром катушки;

D_k – диаметр катушки, см.

Диаметр провода d = 0.41 мм.

k = 3

D_k = 1.5 см, l_k = 1.8 см

k₁= 2.5

Нахождение сопротивления, вносимого собственной ёмкостью катушки индуктивности. В поле собственной ёмкости катушки индуктивности через диэлектрик возникают диэлектрические потери, зависящие от величины этой ёмкости, качества

материала каркаса ( ), изоляции провода и частоты.

, Ом.

Здесь: - ёмкость через диэлектрик, пФ;

L_Г – индуктивность катушки, мкГн;

F – частота, МГц.

Для ПЭЛ:

, – коэффициент, зависящий от конструкции намотки.

Материал каркаса – стеатит.

Общее сопротивление :

Ом.

Добротность катушки индуктивности