60. Признаки сравнения, признак Даламбера и Коши, интегральный признак для числовых рядов с неотрицательными членами.

Признак Даламбера (в предельной форме). Пусть для числового ряда 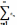с положительными членами существует конечный предел 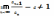. Тогда при d<1 ряд сходится, а при d>1 ряд расходится.

Первый признак сравнения. Пусть члены двух числовых рядов с положительными членами и 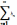удовлетворяют условию a_n<=b_n (n=1,2,…). Тогда из сходимости «большего» ряда следует сходимость «меньшего» ряда , а из расходимости «меньшего» ряда следует расходимость «большего» ряда.

Второй признак сравнения. Пусть для двух числовых рядов с положительными членами и существует конечный предел 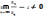. Тогда оба ряда сходятся или расходятся одновременно.

Интегральный признак сходимости. Пусть члены числового ряда a_n=f(n) являются значениями неотрицательной непрерывной функции f(x), монотонно убывающей на луче [1; + oo). Тогда ряд и несобственный интеграл 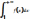сходятся или расходятся одновременно.

Признак Коши. Пусть для числового ряда с положительными членами существует конечный предел 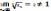. Если к < 1, то ряд сходится, а при к > 1 ряд расходится.

61. Знакопеременные ряды. Абсолютная и условная сходимость.

Числовой ряд, содержащий бесконечное множество положительных и бесконечное множество отрицательных членов, называется знакопеременным. Частным случаем знакопеременного ряда является знакочередующийся ряд, то есть такой ряд, в котором последовательные члены имеют противоположные знаки. Ряд а₁+а₂+…+а_n+…называется абсолютно сходящимся, если ряд |а₁|+|а₂|+…+|а_n|+…также сходится, т.е. сходится ряд, составленный из модулей его членов. Ряд а₁+а₂+…+а_n+…называется условно сходящимся, если сам он сходится, а ряд, составленный из модулей его членов, расходится.

62. Признак Лейбница для знакочередующихся числовых рядов.

Если члены знакочередующегося ряда убывают по абсолютной величине и стремятся к нулю, когда n–>∞, то: 1) ряд сходится; 2) любой остаток ряда не превосходит по абсолютной величине первого из своих членов и имеет одинаковый с ним знак. Или:

1. lb_n+1l<=lb_nl

2. lim n–>∞lb_nl=0