Ранговой коэффициент корреляции Спирмена

Метод ранговой корреляции Спирмена позволяет определить тес­ноту (силу) и направление корреляционной связи между двумя призна­ками или двумя профилями (иерархиями) признаков.

Для подсчета коэффициента ранговой корреляции ранговой корреляции ρ (другое обозначение r_s) необходимо располагать двумя рядами значений, которые могут быть проранжированы. Такими рядами значений мо­гут быть:

1) два признака, измеренные в одной и той же группе испытуемых;

2) две индивидуальные иерархии признаков, выявленные у двух испы­туе­мых по одному и тому же набору признаков (например, личност­ные профили по 16-факторному опроснику Р. Б. Кеттелла, иерархии ценностей по методике Р. Рокича, последовательности предпочтений в выборе из нескольких альтерна­тив и др.);

3) две групповые иерархии признаков;

4) индивидуальная и групповая иерархии признаков.

Во всех четырех случаях значимость полученного коэффициента корреля­ции определяется по количеству ранжированных значений N. В первом случае это количество будет совпадать с объемом выборки N — количеством испытуемых. Во втором случае коли­чеством наблюдений будет количество признаков, составляющих иерархию. В третьем и четвертом случае N — это также количество сопоставляемых призна­ков, а не количество испытуемых в группах.

Коэффициент ранговой корреляции может изменяться от –1 до +1. Положительный знак свидетельствует о прямой зависимости, отрицательный знак — об обратной.

Если абсолютная величина ρ, достигает критического (табличного) значения или пре­вышает его, корреляция достоверна.

Ограничения коэффициента ранговой корреляции

1. По каждой переменной должно быть представлено не менее 5 на­блюде­ний. Верхняя граница выборки определяется имеющимися таб­лицами критиче­ских значений, а именно N<40. Однако возможен расчет коэффициента ранговой корреляции при N>40; в этом случае табличное (критическое) значение следует брать из таблиц критических значений коэффициента линейной корреляции Пирсона, так как при больших N значения коэффициентов Спирмена и Пирсона асимптотически сближаются.

2. Коэффициент ранговой корреляции Спирмена при большом коли­че­стве одинаковых рангов по одной или обеим сопоставляемым пе­ременным дает огрубленные значения. В идеале оба коррелируемых ряда должны представлять собой две последовательности несовпа­дающих значений. В случае если это ус­ловие не соблюдается, необ­ходимо вносить поправку на одинаковые (или связанные) ранги.

Алгоритм расчета ранговой корреляции Спирмена

1. Определить, какие два признака или две иерархии признаков будут участвовать в расчетах. Для удобства расчетов составить таблицу следующего вида:

Таблица 20

№ п/п	X1	X2	R X1	R X2	di	di2
1	2	3	4	5	6	7
1
2
….
N
						Σdi2

Заполнить в таблице столбцы 2 и 3 первичными данными.

2. Проранжировать значения переменной 1, начисляя ранг 1 наименьшему значению, в соответствии с правилами ранжирования. Занести ранги в столбец 4 таблицы по порядку номеров испытуемых или признаков.

3. Проранжировать значения переменной 2 в соответст­вии с теми же правилами. Занести ранги в столбец 5 таблицы по порядку номеров испытуемых или признаков.

4. Под­считать разности рангов в каждой строке таблицы по формуле:

d_i = R _X1 – R _X2 и занести их в столбец 6 таблицы.

5. Возвести каждую разность в квадрат. Эти значения занести в столбец 7 таблицы.

6. Подсчитать сумму квадратов разностей Σd_i²

7. При наличии одинаковых рангов рассчитать поправки:

Т_а= Σ(a³–a)/12

Т_b= Σ( b³–b)/12

где a — объем каждой группы одинаковых рангов в ранговом ряду R _X1 (в столбце 4);

b — объем каждой группы одинаковых рангов в ранговом ряду R _X2 (в столбце 5).

8. Рассчитать коэффициент ранговой корреляции ρ по формуле:

а) при отсутствии одинаковых рангов

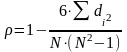
б) при наличии одинаковых рангов

где Σd_i² - сумма квадратов разностей между рангами;

Т_а и Т_b - поправки на одинаковые ранги;

N- количество испытуемых или признаков, которые ранжировались.

9. Правило вывода: Определить по таблице (приложение 3) критическое значение ρ для данного N.

Если ρ превышает критическое значение или по крайней мере равен ему, корреляция достоверно отличается от 0, т.е. взаимосвязь между признаками статистически значима.

Если ρ меньше критического значения, корреляция недостоверно отличается от 0, т.е. взаимосвязь между признаками отсутствует.

Коэффициент ранговой корреляции Кендэлла в лекциях не рассмотрен, так как он применяется значительно реже.