
- •Тема 4. Характеристики взаимосвязи признаков
- •Материалы лекции. Понятие статистической зависимости
- •Общий обзор мер связи
- •Коэффициент контингенции
- •Критерий «хи-квадрат» Пирсона
- •Ранжирование
- •Правила ранжирования
- •Бисериальные коэффициенты корреляции
- •Коэффициент взаимной сопряженности Чупрова
- •Коэффициент взаимной сопряженности Пирсона
- •Ранговой коэффициент корреляции Спирмена
- •Коэффициент линейной корреляции Пирсона
Ранжирование
Ранжирование — это процедура, при которой значения признака заменяются рангами.
Ранг — это порядковое место значения в упорядоченном ряду всех значений.
Правила ранжирования
Меньшему значению присваивается меньший ранг. Наименьшему значению начисляется ранг 1. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений, за исключением тех случаев, которые предусмотрены правилом 2.
Если, например, N=7, то наибольшее значение получит ранг 7 (за исключением тех случаев, которые описаны правилом 2).
В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы были не равны.
Например, три наименьших значения равны 15 секундам. Следующее значение в ряду значений равно 17 секундам. Первые три равных значения занимают в ряду 1-е, 2-е и 3-е места, на 4-м месте стоит следующее по величине значение — 17 секунд и т.д. Каждое из равных значений получает средний ранг 2, а значение 17 — ранг 4.

Допустим, следующие два значения равны 19 секундам. Они занимают 5-е и 6-е места в ряду значений и должны были бы получить 5-й и 6-й ранги, если бы были не равны. Но, поскольку они равны, то получают средний ранг, равный 5,5.

Общая сумма проставленных рангов должна совпадать с расчетной суммой рангов, которая определяется по формуле:
г де
N
— общее количество ранжируемых наблюдений
(значений).
де
N
— общее количество ранжируемых наблюдений
(значений).
Несовпадение реальной и расчетной сумм рангов свидетельствует об ошибке, допущенной при начислении рангов и/или их суммировании. Поэтому прежде чем продолжить работу необходимо найти ошибку и устранить ее.
Бисериальные коэффициенты корреляции
Бисериальные коэффициенты корреляции оценивают зависимость между двумя признаками, один из которых измерен в шкале наименований с двумя градациями признака (дихотомической шкале). Бисериальные коэффициенты корреляции изменяются в диапазоне от -1 до +1, однако следует помнить, что в данном случае знак для интерпретации не имеет значения (это исключение из общего правила).
Рангово-бисериальный коэффициент корреляции используется в том случае, когда второй признак измерен по шкале порядка.
Расчет этого коэффициента производится по формуле:

где
 — средний ранг по тем элементам переменной
Y,
которым соответствует код 1 в переменной
X;
— средний ранг по тем элементам переменной
Y,
которым соответствует код 1 в переменной
X;
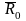 — средний
ранг по тем элементам переменной Y,
которым соответствует код 0 в переменной
X;
— средний
ранг по тем элементам переменной Y,
которым соответствует код 0 в переменной
X;
N — общее количество испытуемых.
Оценку значимости рангово-бисериального коэффициента корреляции произведем с помощью критерия Стьюдента.

где
 —
расчетное значение рангово-бисериального
коэффициента корреляции;
—
расчетное значение рангово-бисериального
коэффициента корреляции;
N — число испытуемых;
tФ — расчетное значение критерия Стьюдента.
Расчеты рангово-бисериального коэффициента корреляции целесообразно вести в следующей таблице (таблица 18):
Таблица 18
хi |
yi |
Ri |
R1 |
R0 |
1 |
y1 |
R1 |
R1 |
|
1 |
y2 |
R2 |
R2 |
|
0 |
y3 |
R3 |
|
R3 |
1 |
y4 |
R4 |
R4 |
|
0 |
y5 |
R5 |
|
R5 |
1 |
y6 |
R6 |
R6 |
|
…… |
…… |
…… |
…… |
…… |
0 |
yN |
RN |
|
RN |
|
|
|
∑R1 |
∑R0 |
Правило принятия решения:
Табличное значение критерия Стьюдента находится по таблице критических значений в зависимости от числа степеней свободы (приложение 5). Число степеней свободы k=N-2.
Если расчетное значение критерия tФ≥ tтабл., то между признаками существует статистическая значимая связь.
Если расчетное значение критерия tФ≤ tтабл., то между признаками статистической связи нет.
Бисериальный коэффициент корреляции используется в том случае, когда второй признак измерен по шкале равных интервалов или шкале равных отношений. Расчет этого коэффициента производится по формуле:

где
 — среднее значение по тем элементам
переменной Y,
которым соответствует код 1 в переменной
X;
— среднее значение по тем элементам
переменной Y,
которым соответствует код 1 в переменной
X;
n1 — количество значений 1 в переменной Х;
 — среднее
значение по тем элементам переменной
Y,
которым соответствует код 0 в переменной
X;
— среднее
значение по тем элементам переменной
Y,
которым соответствует код 0 в переменной
X;
n0 — количество значений 0 в переменной Х;
Sx — стандартное отклонение переменной Y;
N — общее количество испытуемых (N=n1+n0).
Оценку значимости рангово-бисериального коэффициента корреляции произведем с помощью критерия Стьюдента.

где
 —
расчетное значение бисериального
коэффициента корреляции;
—
расчетное значение бисериального
коэффициента корреляции;
N — число испытуемых;
tФ — расчетное значение критерия Стьюдента.
Расчеты бисериального коэффициента корреляции целесообразно вести в таблице следующего вида (таблица 19):
Таблица 19
хi |
yi |
yi– |
(yi– )2 |
yi1 |
yi0 |
1 |
y1 |
|
|
y1 |
|
1 |
y2 |
|
|
y2 |
|
0 |
y3 |
|
|
|
y3 |
1 |
y4 |
|
|
y4 |
|
0 |
y5 |
|
|
|
y5 |
1 |
y6 |
|
|
y6 |
|
…… |
…… |
|
|
…… |
…… |
0 |
yN |
|
|
|
RN |
|
∑yi |
|
∑(yi– )2 |
∑y1 |
∑y0 |
Правило принятия решения:
Табличное значение критерия Стьюдента находится по таблице критических значений в зависимости от числа степеней свободы (приложение 5). Число степеней свободы k=N-2.
Если расчетное значение критерия tФ≥ tтабл., то между признаками существует статистическая значимая связь.
Если расчетное значение критерия tФ≤ tтабл., то между признаками статистической связи нет.

