1. Оцінка варіантів реконструкції азс

1.1 Характеристика системи масового обслуговування (смо)азс

Маємо систему масового обслуговування (СМО) автомобільну заправну станцію (АЗС) з однією колонкою та трьома місцями для очікування. В систему постійно надходять автомобілі, процес надходження вимог у СМО є ймовірнісним. Часові інтервали входження в систему автомобілів будуть випадковими. Вхідний потік є пуассонівським або найпростішим, тому що він має властивості стаціонарності, ординарності і характеризується відсутністю післядії. Випадковий або пуассонівський потік стаціонарний, коли ймовірність надходження певної кількості вимог на певному проміжку часу залежить від величини цього проміжку і не залежить від початку відліку на осі часу. Відсутність післядії полягає в тім, що ймовірність надходження вимог за певний проміжок часу не залежить від того скільки вимог вже надійшло в систему до цього часу. Для характеристики найпростішого потоку необхідно знати його інтенсивність. За характером утворення вхідного потоку АЗС є розімкненою моделлю тому, що кількість джерел, від яких утворюється вхідний потік необмежений (або не визначений).

Модель системи АЗС є двоканальною, бо АЗС має два обслуговуючі прилади (дві заправні колонки). За часом перебування вимог у системі, АЗС є системою з обмеженням черги, а саме система з обмеженням на довжину черги, тому що це система, в якій вимога, що поступає в систему і застає всі канали зайнятими, стає в чергу, якщо її довжина не перевищує наперед відоме значення.

Після реконструкції за першим варіантом кількість місць для очікування залишиться незмінною, тобто їх буде 3, а кількість колонок збільшиться на одну - їх стане 2. АЗС залишиться розімкненою багатоканальною і однотипною за продуктивністю колонок. За часом перебування вимог у системі вона залишається системою з обмеженням черги.

А після реконструкції АЗС за другим варіантом потік залишається пуассонівським, бо кількість колонок залишається незмінною, зміниться лише кількість місць для очікування з 3 до 5. Потік у всіх випадках є найпростішим або пуасоннівським.

1.2. Визначення ефективності базового варіанту азс

Постановка задачі

Дано:

Кількість колонок на АЗС - n=2

Кількість місць для очікування заправки - m=4

Інтенсивність потоку - =1,35

Середній час заправки 1 автомобіля - tобс.=1.5 хв

1.2.1. Визначаємо інтенсивність обслуговування за формулою:

(1.1)

1.2.2. Визначаємо параметр потоку а за формулою:

; (1.2)

де а­ - середнє число заявок, що припадає на середній час обслуговування 1-єї заявки

1.2.3. Визначаємо імовірність Р_відм того, що заявці буде відмовлено в обслуговуванні за формулою:

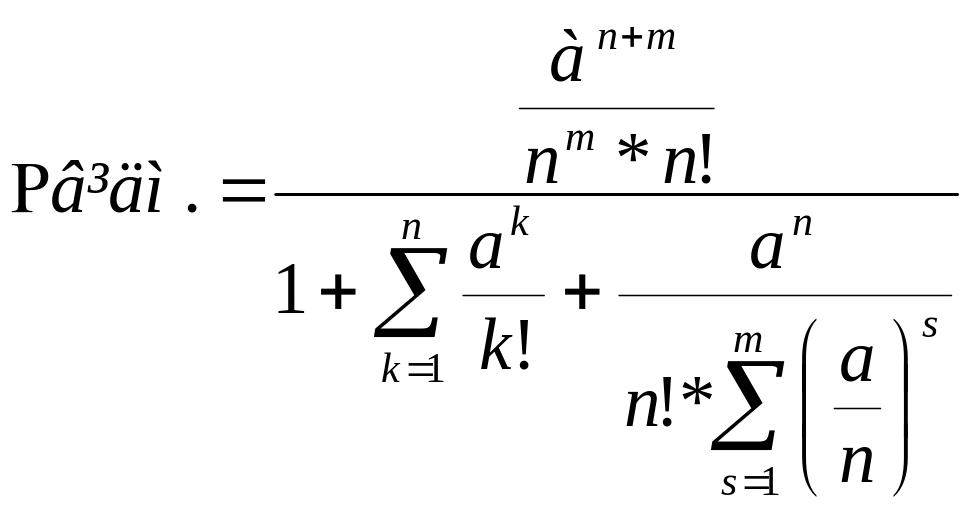(1.3)

де n – кількість колонок на АЗС

m – кількість місць для очікування;

к - кількість зайнятих каналів;

s – кількість зайнятих місць для очікування.

Це означає, що із 100 автомобілів 16 покинуть АЗС не обслуговані.

1.2.4. Визначаємо імовірність того, що автомобілі будуть обслуговані Р_обс за формулою:

(1.4)

(1.5)

Це означає , що із 100 автомобілів 84, що приїжджають на АЗС, будуть обслуговані.

1.2.5. За середньою інтенсивністю прибуття автомобілів на АЗС =1,15 за 1 день матимемо таку кількість автомобілів V_д:

(1.6)

де t – тривалість робочого дня, год.

1.2.6. Визначаємо кількість автомобілів які надходять на АЗС за 1 рік V_р:

(1.7)

1.2.8. Визначаємо кількість обслугованих автомобілів за рік V_обс:

(1.8)

1.2.9. Визначаємо річний прибуток П_р за формулою:

(1.9)

ПР= 299434*0,5=149717

В базовому варіанті прибуток АЗС складає149717у .о.

1.2.10. Висновок: при базовому варіанті реконструкції:

1. Ймовірність відмови (Рвід), тобто ймовірність того, що заявка для АЗС буде втраченою складає 15.6%;

2. Ймовірність Робс ,тобто ймовірність того, що автомобіль буде заправлений становить 84.4%;

3. Параметр потоку а=2.01;

Інтенсивність обслуговування µ=0.67 авт/хв;

4. Прибуток Пр АЗС в базовому варіанті складе 149717у.о.

1.2.1. Розглядаємо ефективність базового варіанту для цього будуємо граф станів і схему системи масового обслуговування ( рис 1.1 і рис1.2 ).

Для знаходження рішення використовують метод теорії масового обслуговування, а раціональний варіант методом ітерацій.

Базовий варіант (без реконструкції), маємо модель, одно канальної СМО з обмеженням черги (n=2, m=4)

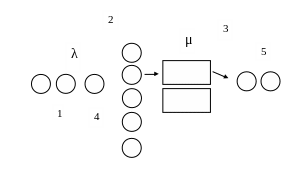
Рис.1.1 Схема системи масового обслуговування базового стану АЗС

1-вхідний потік; 2-місця для очікування; 3-обслуговуючі апарати;

4-заявка покидає систему; 5-вихідний потік; λ-інтенсивність вхідного потоку;

μ-інтенсивність обслуговування

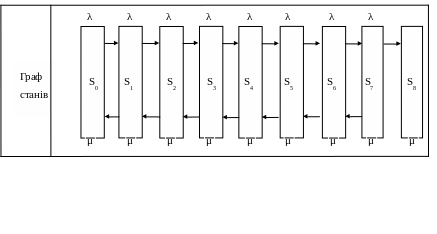
Рис.1.2. Розмічений граф станів базового варіанту АЗС.

S₀-система вільна; S₁-завантажений стан 1 колонки; S₂-завантажений стан 2 колонки ; S₃-заняте 1 місце для очікування; ; S₄ -заняте 2 місце для очікування;

S₆ -заняте 3 місце для очікування; ; S₇-заняте 4 місце для очікування автомобіль;

S₈-автомобіль покидае систему;λ-інтенсивність вхідного потоку;

μ-інтенсивність обслуговуванн.