Методы формирования сложных, объемных, криволинейных поверхностей. Назначение, конструкция и кинематическая схема многофункциональных обрабатывающих центров
5.1. Методы формирования сложных, объемных, криволинейных поверхностей
5.1.1. Геометрическое и математическое моделирование
Формирование сложных криволинейных поверхностей - неразрывно связано со всеми отраслями и видами производства. За последнее десятилетие в самолетостроении, кораблестроении, машиностроении и станкостроительной промышленности стали широко применяться изделия с квазивинтовыми поверхностями, имеющими сложный криволинейный профиль, криволинейную ось и переменный шаг.
Внедрение более современной технологии обработки изделий в гибких автоматизированных производствах, на обрабатывающих модулях, на станках ЧПУ, в свою очередь, требует разработки эффективных методов геометрического и математического моделирования квазивинтовых поверхностей.
Геометрическое и математическое моделирование квазивинтовых поверхностей криволинейным преобразованием включает круговое и поступательное преобразование исходной криволинейной поверхности Ф(s, t) относительно криволинейной оси m(u).
Рассмотрим геометрическое моделирование квазивинтовых поверхностей S* круговым преобразованием исходной криволинейной поверхности Ф (рис. 1).
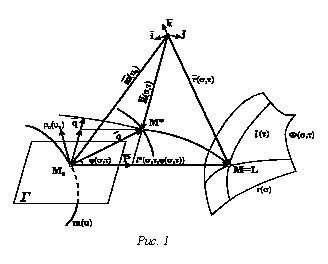
Пусть исходная криволинейная поверхность Ф(s,t)задана радиусом-вектором r(s,t), криволинейной осью m(u), определяемой радиусом-вектором m(u).
Поверхность S* формируется вращением относительно оси m(u) каждой точки заданной исходной поверхности Ф на угол j(s,t), зависящий, в общем случае, от положения точки на исходной поверхности Ф.
Выберем на образующей l(t) поверхности
Ф некоторую точку М и найдем ее проекцию
М0 на ось m(u). Повернем точку М вокруг
оси, совпадающей с касательной r0(u0) к
криволинейной
оси m(u) в точке М0, на некоторый угол
j(s,t). Описанное круговое преобразование
точки М определяет положение точки М*.
Осуществляя аналогичные преобразования
всех других точек Мi образующей поверхности
Ф получим обобщенную линию поверхности
S*.
Каждая линия l(t) криволинейной исходной поверхности Ф преобразуется в обобщенную линию l*(s,t,j(s,t)). Семейство линий l* задает поверхность S*.
Для формирования математической модели поверхности S* считаем, что точка М задана радиусом-вектором r(s,t), где s и t криволинейные координаты точки М на поверхности Ф (см. рисунок 1). Пусть также задана некоторая ось m(u) своим радиусом-вектором m(u), где u определяет положение точки на оси m(u). Пусть положение точки М0 на оси m(u) определяется значением параметра u0. Обозначим через r0(u0) единичный касательный вектор к криволинейной оси m(u) в точке М0, тогда значение u0 удовлетворяет следующему соотношению:
m(u0) · r(u0) = 0
и, следовательно, u0 = u0( s,t)
Пусть R(s,t) определяет положение точки М* . Тогда R(s,t) = m(u) + (r(s,t ) - m(u)·cosj + r (u)(r(u)·r(s,t - m(u)))·sinj , (1)
где j = j(s,t) - угол вращения точки М, лежащей на поверхности Ф;
m(u) - радиус-вектор криволинейной оси m;
r0(u0) - единичный вектор касательной к оси m;
r(s,t) - радиус-вектор точки М на поверхности Ф;
s,t- криволинейные координаты точки М.
Следующим обобщением предложенного метода формирования поверхностей является их геометрическое моделирование с помощью криволинейного преобразования.
Рассмотрим геометрическое моделирование квазивинтовых поверхностей S криволинейным преобразованием исходной криволинейной поверхности Ф (рис. 2).
Выберем на образующей l(t) исходной поверхности Ф некоторую точку М и найдем ее проекцию М0 на кривую m. Точка М участвует одновременно в двух движениях: в поступательном и вращательном - вокруг оси r(u), совпадающей с касательной к кривой m в точке М0. Осуществляя аналогичные криволинейные преобразования всех других точек образующей l(t) поверхности Ф получим винтовую линию поверхности S. Каждая линия l(t ) криволинейной исходной поверхности Ф преобразуется в обобщенную винтовую линию l(s,t,j(s,t)) c переменным шагом. Семейство линий l(s,t,j(s,t)) задает квазивинтовую поверхность S.
Для формирования математической модели
поверхности S будем считать, что точка
М задана радиусом-вектором r(s,t), где s и
t - криволинейные координаты точки на
поверхности Ф. Пусть также задана
некоторая криволинейная ось m(u) своим
радиус-вектором m(u), где u определяет
положение точки на кривой m. Пусть
положение точки М0 на оси m(u) определяет
значение параметра u0. Обозначим через
r0(u0) единичный 
касательный
вектор к оси m(u) в точке М0, тогда значение
u0 удовлетворяет следующему соотношению:
(r(s,t) - m(u0)·r(u0)) = 0
и, следовательно, u0 = u0(s,t )
Второе поступательное движение точки М относительно оси m(u) определяется уравнением h(s,t)·r(u) (2) . Учитывая уравнения (1), окончательно получим: R(s,t) = m(u) + (r(s,t ) - m(u)·cosj + r(u)(r(u)· (r(s,t) - m(u)))·sinj + h(s,t)·r(u) . (2)
Разработанный метод криволинейных преобразований позволяет получать математическую модель гребных винтов применительно к современным технологиям обработки на станках ЧПУ [1], формировать сложные криволинейные профили многозаходных чистовых червячных фрез с пространственной режущей кромкой [2, 3], создавать новые виды зубчатых передач без интерференции [4].