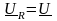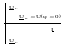- •1) Законы Электротехники (закон Ома; 1-й закон Кирхгофа; 2-й закон Кирхгофа);
- •2)Методы расчета эл.Цепей
- •6) Основные термины и определения, применяемые в электротехнике.
- •8)Закон электромагнитной индукции
- •9)Классификация и основные характеристики электротехнических материалов
- •10)Алгоритм расчета электрической цепи методом эквивалентных преобразований.
- •11) Алгоритм расчета электрической цепи методом непосредственного применения законов Кирхгофа
- •12)Алгоритм расчета электрической цепи методом контурных токов.
- •1 3) Алгоритм расчета электрической цепи методом наложения.
- •14) Алгоритм расчета электрической цепи методом двух узлов.
- •15) Алгоритм расчета электрической цепи методом эквивалентного генератора
- •16) Баланс мощности электрической цепи.
- •17) Построение потенциальной диаграммы.
- •18) Построение графа электрической цепи.
- •19)Перечислите режимы работы источников в линейных электрических цепях постоянного тока.
- •20)Линейные цепи переменного тока. Основные параметры, характеризующие синусоидальную величину (начальная фаза, амплитуда, период, частота, мгновенное и действующее значения, сдвиг фаз).
- •21)Анализ электрического состояния цепи переменного тока. Цепь с резистивным элементом. Основные формулы. Временные и векторные диаграммы.
- •22)Анализ электрического состояния цепи переменного тока. Цепь с индуктивным элементом. Основные формулы. Временные и векторные диаграммы.
- •23) Анализ электрического состояния цепи переменного тока. Цепь с конденсатором. Основные формулы. Временные и векторные диаграммы.
- •24)Цепь с последовательным соединением элементов r, l, c. Комплексное и полное сопротивление цепи. Закон Ома в комплексной форме. Векторная диаграмма.
- •25)Резонанс напряжений в цепи переменного тока. Его характерные особенности. Условия возникновения и практическое значение.
- •26) Расчет цепи переменного тока с использованием комплексных чисел. Формы представления комплексного числа и их взаимосвязь.
- •27)Свойства цепей с параллельным соединением элементов. Резонанс токов. Условия возникновения. Векторные диаграммы.
- •28)Коэффициент мощности и его экономическое значение.
- •46) Мощности в цепи переменного тока (активная, реактивная и полная). Треугольник мощностей. Примеры расчета.
- •51)Характеристики ферромагнитных материалов. Кривые намагничивания. Гистерезис.
- •52)Методы расчета нелинейных цепей постоянного тока.
- •53)Расчет цепи с последовательным соединением нелинейных элементов
- •54)Расчет цепи с параллельным соединением нелинейных элементов.
- •55) Смешанное соединение нелинейных элементов
- •56)Магнитные цепи. Основные характеристики. Закон полного тока.
- •57)Расчет магнитной цепи. Прямая задача.
- •58) Расчет магнитной цепи. Обратная задача
- •3. По кривой намагничивания определить напряженности магнитного поля для всех участков цепи.
24)Цепь с последовательным соединением элементов r, l, c. Комплексное и полное сопротивление цепи. Закон Ома в комплексной форме. Векторная диаграмма.
Если
к участку с последовательным соединением
элементов R,
L,
C
приложено синусоидальное напряжение
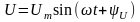 ,
то и ток в цепи синусоидальный
,
то и ток в цепи синусоидальный
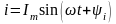 .
.
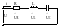
На каждом из элементов будет падать напряжение
По
второму закону Кирхгофа для мгновенных
значений
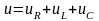
Для комплексных выражений
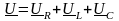
Подставив
в выражение
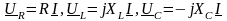 Получим
закон Ома в комплексной форме:
Получим
закон Ома в комплексной форме:
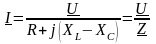 ,
,
где
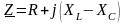 - комплексное сопротивление;
- комплексное сопротивление;
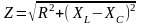 -
модуль комплексного сопротивления,
или полныое сопротивление;
-
модуль комплексного сопротивления,
или полныое сопротивление;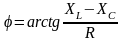 -
аргумент комплексного сопротивления.
-
аргумент комплексного сопротивления.
знак угла сдвига фаз между током и напряжением определяется знаком реактивного сопротивления
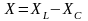 ,
,
Если
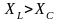 ,
то нагрузка в цепи имеет активно-индуктивный
характер, ток по фазе отстает от
напряжения на угол
,
то нагрузка в цепи имеет активно-индуктивный
характер, ток по фазе отстает от
напряжения на угол
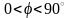
Если
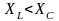 ,
то нагрузка имеет активно-емкостный
характер, ток по фазе опережает
напряжение.
,
то нагрузка имеет активно-емкостный
характер, ток по фазе опережает
напряжение.
Порядок построения векторной диаграммы:
-
строим вектор тока
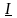 ;-
строим вектор падения напряжения
;-
строим вектор падения напряжения
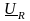 на активном сопротивлении (он совпадает
по направлению с вектором тока
,
сдвиг фаз равен нулю);- строим вектор
падения напряжения
на активном сопротивлении (он совпадает
по направлению с вектором тока
,
сдвиг фаз равен нулю);- строим вектор
падения напряжения
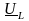 на
индуктивном сопротивлении (опережает
по фазе вектор тока на 90);-
строим вектор падения напряжения
на
индуктивном сопротивлении (опережает
по фазе вектор тока на 90);-
строим вектор падения напряжения
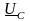 на емкостном сопротивлении (конденсатора)
(он отстает по фазе от вектора тока на
90);
на емкостном сопротивлении (конденсатора)
(он отстает по фазе от вектора тока на
90);
-
складывая векторы
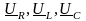 ,
получаем вектор общего напряжения
,
получаем вектор общего напряжения
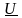 ,который
опережает по фазе на угол
вектор тока
,
что указывает на активно-индуктивный
характер нагрузки.
,который
опережает по фазе на угол
вектор тока
,
что указывает на активно-индуктивный
характер нагрузки.
25)Резонанс напряжений в цепи переменного тока. Его характерные особенности. Условия возникновения и практическое значение.
Резонансом в электрических цепях называется режим участка электрической цепи, содержащей индуктивный (ХL) и емкостной (ХС) элементы, при котором угол сдвига фаз между напряжением и током равен нулю (). Различают резонанс напряжений и резонанс токов.
При
этом индуктивное сопротивление равно
емкостному, то есть
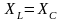 .
.
Угол сдвига фаз определяется по формуле:
.
При
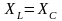 или можно записать
или можно записать
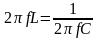
Из последнего соотношения следует, что резонанс напряжения в цепи можно достигнуть следующими способами:
изменением индуктивности L катушки;
изменением электрической емкости С конденсатора;
изменением частоты тока f питающей сети.
Условия возникновения резонанса:
-переменный ток
-наличие конденсаторов(XC) и катушки (XL) в цепи
-XL=XC
-последовательное соединение
Характерные особенности резонанса напряжений
1. Полное сопротивление Z цепи при резонансе равно активному сопротивлению
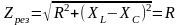 .
.
2.
Результирующий ток в цепи имеет
максимальное значение
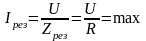
Зависимость тока I от частоты f имеет вид:
3.
Напряжение на участке с активным
сопротивлением R
равно напряжению питания U
и совпадает с ним по фазе
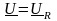 .
.
4.
Активная мощность при резонансе имеет
максимальное значение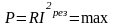 .
.
Можно предположить, что в цепи существует следующее соотношение между активным (R) и реактивными сопротивлениями (XL и XC)
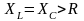 ,
,
тогда
можно записать
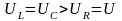 .
.
То есть напряжения на участках с реактивными элементами (UL и UC) будут больше напряжения питания U.
Свойство усиления напряжения на реактивных элементах при резонансе напряжения используется в технике.
Коэффициент
усиления напряжения равен добротности
Q
контура
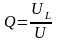
Однако повышенное напряжение на реактивных элементах может привести к пробою электрической изоляции проводов и представлять опасность для обслуживающего персонала.
Векторная диаграмма при резонансе напряжений строится с учетом особенностей режима резонанса
=0,
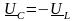 ,
,