Оценка зависимости между признаками

Изложенные выше методы статистического анализа дают возможность изучать изменчивость био­логических объектов по отдельным признакам – весу, размерам, плодовитости, физиологическим показателям и др. Однако в ряде случаев важно знать, какова зависимость меж­ду вариацией двух или нескольких признаков, изменяются ли две переменные самостоятельно, независимо друг от друга, или варьирование одного признака в какой-то степени связано с изменчивостью другого. В качестве второй переменной часто выступает какой-либо фактор среды.

Задачу исследования зависимостей можно рассматривать как развитие метода дисперсионного анализа, решающего задачу сравнения нескольких выборок, т. е. изучающего влияния фактора на признак. Техника дисперсионного анализа имеет две особенности. Фактор (или факториальный признак) задан дискретно, в виде градаций, или «доз». Когда исследуется фактор, заданный качественно, то разбиение на градации всего диапазона его действия оказывается очень эффективным способом создания подобия количественной переменной. Но при изучении количественно заданного фактора в грубой градуальной схеме дисперсионного анализа утрачивается часть информации, которая содержится в исходных выборках и которую можно было бы использовать. Кроме этого, дисперсионный анализ явным образом не учитывает тенденции изменения среднего уровня признака при изменении уровня фактора, не содержит показателя характера (знака) зависимости признака от фактора. Все эти «недостатки» дисперсионного анализа не характерны для методов изучения сопряженной изменчивости – корреляционного и регрессионного анализов.

Способ представления отдельных наблюдений здесь меняется: каждая варианта рассматривается как носитель двух численных характеристик объекта измерения, двух зависимых значений случайной величины. Если выше мы отождествляли отдельное значение с отдельной вариантой, то теперь мы рассматриваем варианту как некоторое тело, обладающее минимум двумя зарегистрированными качествами, различными у разных вариант:

Например, для любого животного можно определить массу (M) и длину (L) тела; отдельная варианта будет нести два значения (L, M). При этом множество вариант выборки можно отобразить графически как точки на плоскости осей двух признаков M и L. Вся выборка предстанет в виде множества точек на плоскости (двумерное рассеяние). Как видно на диаграмме (рис. 10), «облако» вариант вытянуто в направлении диагонали облака точек. Справа вверху находятся варианты с высокими значениями и размеров и массы тела, в левом нижнем углу – с наименьшими значениями. В центре расположены варианты с промежуточными, средними значениями.

Рис. 10. Область рассеяния вариант

В первом приближении можно сказать, что двумерное распределение –это ординация вариант на плоскости осей двух признаков. Помимо рассеяния на плоскости, в определение двумерного распределения входит и частота встречаемости отдельных значений (a). Если признаки x и y теоретически подчиняются нормальному закону, тогда скопление вариант в трех осях (оси признаков x, y и частоты а) образует весьма странный «гребень», растянутое в пространстве выпуклое нормальное распределение (рис. 11). Однако в реальности такой идеальной картины получить никогда не удается, приходится ориентироваться только на плоскую фигуру рассеяния немногочисленных вариант. Если область, занятую вариантами, очертить по периферии плавной линией, мы получим вытянутую фигуру, эллипс, ограничивающий область рассеяния вариант, эллипс рассеяния. Эллипс рассеяния – это область распространения вариант одной совокупности.

М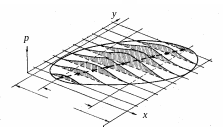 ожно видеть, что в нашем примере признаки связаны друг с другом – есть общая тенденция: чем больше длина тела, тем больше вес; эта зависимость не очень жесткая, она размыта индивидуальными особенностями объектов (вариант).

Рис. 11. Двумерное распределение

В двумерном распределении проявляются два эффекта: синхронное изменение двух признаков и размывание этой синхронности, т. е. действие факторов сопряжения признаков вдоль оси эллипса и действие случайных факторов – поперек нее.