
- •Обоснование метода решения
- •1.2. Составление расчетной схемы
- •Для полученной плоской системы сил составляем три уравнения равновесия:
- •Аналитическое решение
- •Определение геометрических характеристик сечения
- •Обоснование метода решения
- •Определение геометрических характеристик сечения
- •Подготовка задачи решению задачи в MathCad
- •Расчет балки на изгиб…………………………………………
- •4.1 Обоснование метода решения
- •4.2 Составление расчетной схемы и аналитическое решение
- •4.3 Подготовка задачи решению задачи в MathCad2001

РЕФЕРАТ |
Пояснительная записка содержит __ листов, __ рисунков, __ таблиц, ___ использованных источников, __ приложений.
составная конструкция, реакции связей, продольная сила, поперечная сила, изгибающий момент, геометрические характеристики плоского сечения, нормальное напряжение, прочность.
Предметом исследования является прочность составной конструкции.
Цель работы – применение общих положений механики деформируемого тела к исследованию прочности.
В первой части работы…….
Во второй части работы……
В третьей части работы……
В четвертой части работы…..
Исследование проводилось при помощи аналитических расчетов, построения эпюр, пакета прикладных программ MathCad 14.
Содержание
Введение……………………………………………………………………
Определение реакций внешних опор и усилий в местах
соединения звеньев составной конструкции ……………………….
1.1 Обоснование метода решения…………………………………..….
1.2 Составление расчетной схемы…………………..…………………
1.3 Аналитическое решение……………………..……………………
1.4 Подготовка задачи решению задачи в MathCad……………
Определение геометрических характеристик сечения…………………….
2.1 Обоснование метода решения………………………………….…
2.2 Определение геометрических характеристик сечения …………
2.3 Подготовка задачи решению задачи в MathCad……………
3. Расчет балки на растяжение-сжатие…………………………………………
3.1 Обоснование метода решения………………………………….…
3.2 Составление расчетной схемы и аналитическое решение………
3.3 Подготовка задачи решению задачи в MathCad……………
4. Расчет балки на изгиб…………………………………………
4.1 Обоснование метода решения………………………………….…
4.2 Составление расчетной схемы и аналитическое решение………
4.3 Подготовка задачи решению задачи в MathCad……………
Заключение………………………………………………………………
Список использованных источников………………..………………….
Приложение …………………………………………………………...
Введение
Определение реакций внешних опор и усилий в местах соединения звеньев составной конструкции
Обоснование метода решения
Равномерно распределенную нагрузку заменяем сосредоточенной силой, приложенной в геометрическом центре нагруженного участка и имеющей такое же направление.
По принципу освобождаемости от связей опора должна быть заменена реакциями связей, препятствующими перемещению точки конструкции, в которой установлена опора.
Т.к., конструкция состоит из нескольких твердых тел, соединенных между собой двухсторонними связями, то ее разделяем на части и составляем уравнения равновесия для каждой части отдельно, а затем решаем полученные системы уравнений совместно.
Для плоской системы сил условия равновесия могут быть записаны в одной из трех форм:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
;
;
![]() ;
;
![]() ;
;
;
;
![]() .
.
Для определения моментов сил относительно точки используется теорема Вариньона: если система сил имеет равнодействующую, то момент этой равнодействующей относительно любой точки равен сумме моментов составляющих относительно этой же точки.
Силы, приложенные к балке под углом, отличным от прямого, раскладываем на составляющие, параллельные координатным осям.
1.2. Составление расчетной схемы
Для определения реакций разделим систему на составные части и рассмотрим сначала равновесие стержня DE (рис. 203).
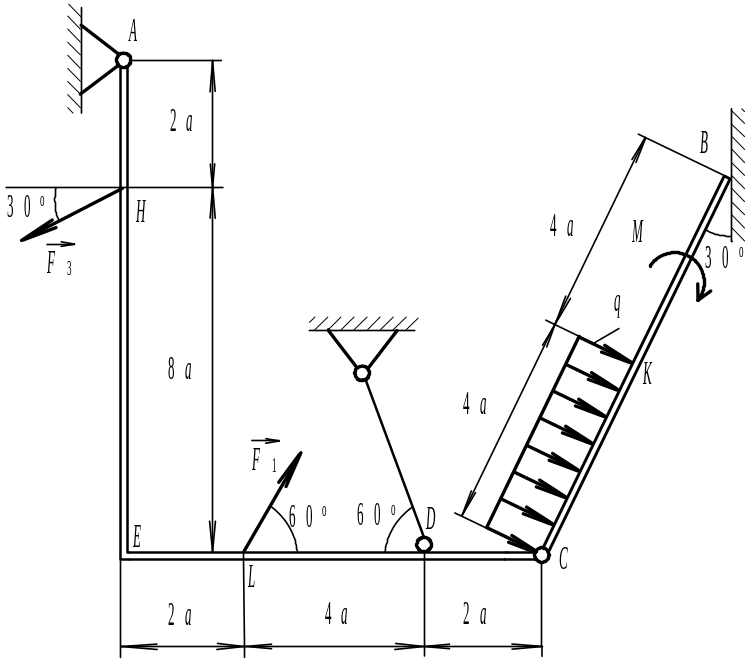
Рис. 1.
Проведем
координатные оси xy
и изобразим действующие на стержень
силы: пару сил с моментом
![]() и равномерно распределенную нагрузку,
которую заменяем силой
и равномерно распределенную нагрузку,
которую заменяем силой
![]() ,
приложенной к середине участка CK
(численно
,
приложенной к середине участка CK
(численно
![]() кН), реакцию
кН), реакцию
![]() ,
направленную перпендикулярно опорной
поверхности, и составляющие
,
направленную перпендикулярно опорной
поверхности, и составляющие
![]() и
и
![]() реакции шарнира С.
реакции шарнира С.
Для полученной плоской системы сил составляем три уравнения равновесия:
![]() ,
,
![]() ;
(435)
;
(435)
![]() ,
,
![]() ;
(436)
;
(436)
![]() ,
,
![]() .
(437)
.
(437)
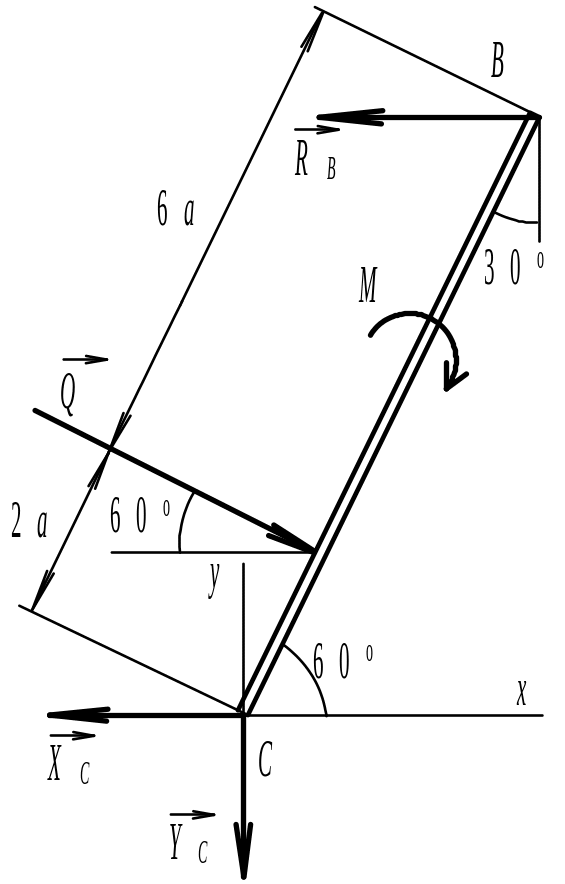
Рис. 2.
2.
Теперь рассмотрим равновесие угольника
(рис 204). На него действуют силы
![]() и
и
![]() реакция стержня
,
направленная вдоль оси стержня (полагаем,
что стержень находится под сжимающей
нагрузкой), реакция неподвижного шарнира,
слагающаяся из силы, которую представим
составляющими
реакция стержня
,
направленная вдоль оси стержня (полагаем,
что стержень находится под сжимающей
нагрузкой), реакция неподвижного шарнира,
слагающаяся из силы, которую представим
составляющими
![]() и
и
![]() и составляющие
и
реакции шарнира С.
и составляющие
и
реакции шарнира С.
Для этой плоской системы сил тоже составляем три уравнения равновесия:
,
![]() ;
(438)
;
(438)
,
![]() ;
(439)
;
(439)
![]() ,
,
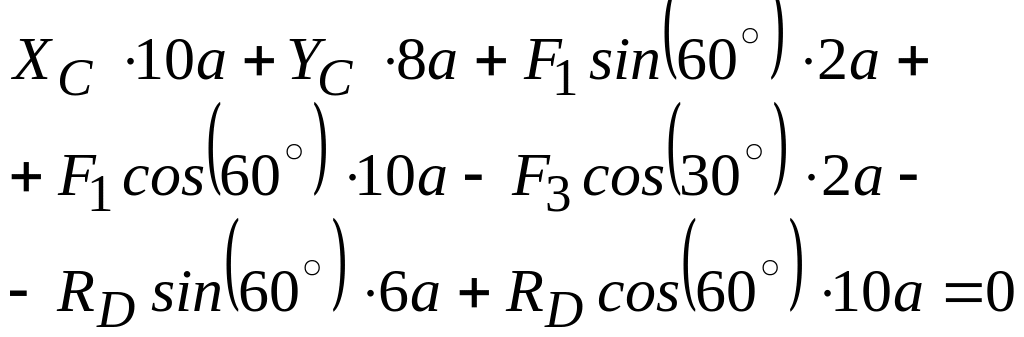 .
(440)
.
(440)

Рис. 3.
Аналитическое решение
Из
(437)
![]() кН.
кН.
Из
(436)
![]()
Из
(435)
![]() кН.
кН.
Из (440)
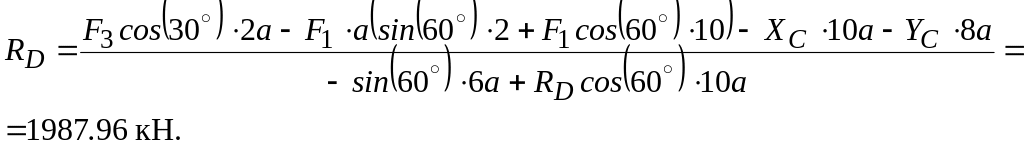
Из
(439)
![]() кН.
кН.
Из
(438)
![]() кН.
кН.
Подготовка задачи к решению в
Составляем матрицу коэффициентов левой
части системы уравнений
![]() и вектор столбец правой части
и вектор столбец правой части
![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
