3. Расчет электрической цепи методом наложения ( суперпозиции ) не делать
сделаем 1-шаг. Предположим, что ЭДС Е = 0.
Тогда схему на рис. 3 можно заменить эквивалентной схемой на рис. 5:
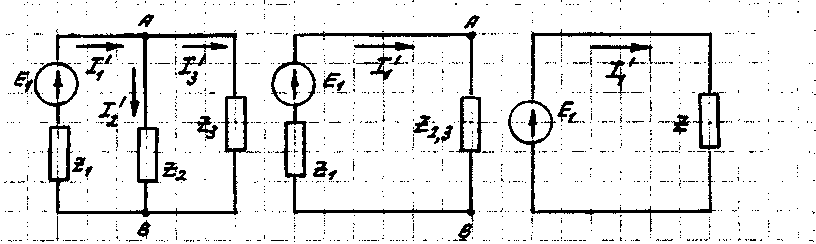
Рис. 5 Рис. 6 Рис. 7
2. найдем токи в схеме на рис. 5 методом свертывания электрической цепи. Суть
«свертывания» состоит в упрощении схемы цепи путем перехода от смешанного соедине
ния сопротивлений к последовательному.
3. в схеме на рис. 5 сопротивления z и z соединены параллельно, заменим их эквива-
лентным сопротивлением
z = ( z * z ) / (z + z ) = ĵ35 ( 20 + ĵ15 ) / ( ĵ35 + 20 + ĵ15 ) =
= ... = 8,45 + ĵ13,88.
В результате такой замены схему на рис. 5 можно представить схемой на рис. 6.
в схеме на рис. 6 сопротивления z и z соединены последовательно, заменим
их эквивалентным сопротивлением всей цепи
z = z + z = ( 20 - ĵ5 ) + ( 8,45 + ĵ 13,88 ) = 28,45 + ĵ8,88
теперь схему на рис. 6 можно заменить схемой на рис. 7, состоящей из источни-
ка ЭДС Е и эквивалентного сопротивления всей цепи z.
для такой цепи применим закон Ома для цепи, в соответствии с которым ток
через источник Е , или, что одно и то же, первый частичный ток левой ветви
I' = Е / z = ĵ40 / ( 28,45 + ĵ8,88 ) = … = 0,4 + ĵ1,28.
чтобы найти первые частичные токи средней и правой ветвей I' и I' , сначала
найдем напряжение
U
=
I'
*
z
= ( 0,4 + ĵ1,28 ) ( 8,45 + ĵ8,8 ) = … = -
14,38 + ĵ16,36
9. теперь, по закону Ома для участка цепи ( рис. 5 ) найдем первые частичные токи
I' = U / z = ( - 14,38 + ĵ16,36 ) / (ĵ35 ) = … = 0,4674 + ĵ0,41.
I' = U / z = ( - 14,38 + ĵ16,36 ) / ( 20 + ĵ15 ) = … = - 0,076 + ĵ0,8767
проверим правильность расчета токов 1-го шага, для чего применим 1-й закон
Кирхгофа для узла «А»:
I' = I' + I' , или в числах : 0,4 + ĵ1,28 ≈ ( 0,4674 + ĵ0,41 ) + (- 0,076 + + ĵ0,8767 ) =
= 0,4004 + ĵ 1,2787.
Сравнивая по отдельности действительные и мнимые части левой и правой части
равенства, можно убедиться в их незначительном расхождении: 0,4 ≈ 0,4004 и ĵ1,28 ≈
≈ ĵ1,2787.
Сделаем 2-й шаг. Предположим, что Е = 0. Тогда схему на рис. 3 можно заме
нить схемой на рис. 8.
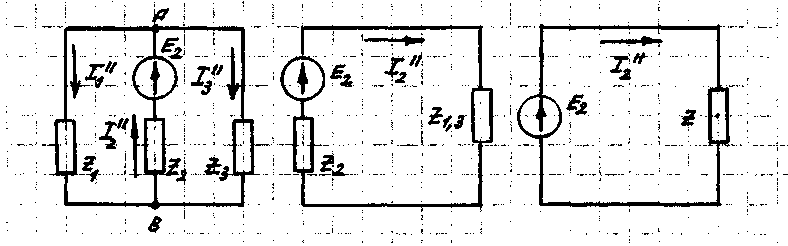
Рис.8 Рис. 9 Рис. 10
Последующий расчет проводим в такой же последовательности, что и в 1-м шаге.
Сопротивления z и z соединены параллельно, их эквивалентное сопротивле-
ние
z = ( z * z ) / ( z + z ) = ( 20 – ĵ5 )*( 20 + ĵ15 ) / [ ( 20 – ĵ5 ) + ( 20 + ĵ15 )]=
= … = 12,35 + ĵ1,91
В результате от схемы на рис. 8 можно перейти к схеме на рис. 9.
в схеме на рис. 9 сопротивления z и z соединены последовательно, их эквива
лентное сопротивление
z = z + z = ( 12,35 +ĵ1,91 ) + ( ĵ 35 ) = 12,35 + ĵ36,9.
теперь схему на рис. 9 можно заменить схемой на рис. 10, состоящей из источни
ка ЭДС Е и эквивалентного сопротивления всей цепи z.
для такой цепи применим закон Ома для цепи, в соответствии с которым ток
через источник Е , или, что одно и то же, второй частичный ток средней ветви
I" = Е / z = ( - 42,42 + ĵ 42,42 ) / ( 12,35 + ĵ36,9 ) = … = 0,688 + ĵ1,38.
чтобы найти вторые частичные токи левой и правой ветвей I' и I' , сначала
найдем напряжение между точками «А» и «В»
U = I" * z = ( 0,688 + ĵ1,38 ) ( 12,35 + ĵ1,91 ) = … = 5,86 + ĵ18,36
9. теперь, по закону Ома для участка цепи ( рис. 5 ) найдем вторые частичные токи
левой и правой ветвей
I" = U / z = ( 5,86 + ĵ18,36 ) / ( 20 – ĵ5 ) = … = 0,06 + ĵ0,933
I" = U / z = ( 5,86 + ĵ18,36 ) / ( 20 + ĵ5 ) = … = 0,628 + ĵ0,4468
проверим правильность расчета токов 2-го шага, для чего применим 1-й закон
Кирхгофа для узла «А»:
I" = I" + I" , или в числах : 0,688 + ĵ1,38 ≈ ( 0,06 + ĵ0,933 ) + + ( 0,628 + ĵ0,4468 ) = 0,688 + ĵ 1,3798.
Сравнивая по отдельности действительные и мнимые части левой и правой части
равенства, можно убедиться в их незначительном расхождении: 0,688 = 0,688 и ĵ1,38 ≈ ĵ1,3798.
Наложим друг на друга частичные токи в ветвях, с учетом их направления:
I = I' - I" = ( 0,4 + ĵ1,28 ) – ( 0,06 + ĵ0,933 ) = 0,34 + ĵ0,347;
I = I" - I' = ( 0,688 + ĵ1,38 ) – ( 0,4674 + ĵ0,41 ) = 0,22 + ĵ0,97;
I = I' + I" = ( - 0,0673 + ĵ0,8767 ) + ( 0,628 + ĵ0,4468 ) = 0,56 + ĵ1,335.
Проверим правильность всего расчета в целом, применив 1-й закон Кирхгофа
для узла «А»
I = I + I , или в числах: 0,56 + ĵ1,335 ≈ ( 0,34 + ĵ0,347 ) + ( 0,22 + ĵ0,97 ) =
= 0,56 + ĵ1,335.