Рассчитать токи всех ветвей такими методами:
.1. контурных токов;
.2. наложения ( суперпозиции ); не делать
.3. узлового напряжения.
Определить режим работы каждого источника эдс;
Составить баланс мощностей.
Исходные данные:
Е = 40 В; Е = 60 В; Е = 0; Е = 0; Е = 120 В; Е = 75 В; Е = 15 В;
φ = + 90º; φ = + 135º; φ = + 75º; φ = + 90º; φ = + 150º; φ = - 180º; φ = 0º;
r = 20 Ом; r = 0; r = 10 Ом; r = 10 Ом; r = ∞; r = 20 Ом; r = 30 Ом;
х
=
20 Ом; х
=
35 Ом; х
=
30 Ом; х
=
40 Ом; х
=
45 Ом; х
=
∞; х
=
35 Ом;
х
=
25 Ом; х
=
0; х
=
15 Ом; х
=
15 Ом; х
=
25 Ом; х
=
10 Ом; х
=
20 Ом.
Рис. 1. Исходная принципиальная электрическая схема цепи переменного тока
Решение
1. Составление принципиальной электрической схемы
1.1. Используя исходные данные, упростим схему на рис. 1.
Поскольку r = ∞ и х = ∞, в месте включения этих элементов образуем разрывы цепей.
Поскольку r = 0 и х = 0, в месте включения этих элементов ставим перемычки.
В результате исходная схема на рис. 1 преобразуется в промежуточную схему на рис.2.
Рис. 2. Промежуточная схема Рис. 3. Рабочая схема
электрической цепи электрической цепи
1.2. Найдем полные сопротивления каждой из 3-х ветвей:
сопротивление левой ветви z = r + ĵ ( х - х ) = 20 + + ĵ ( 2- - 25 ) = 20 – ĵ5;
cопротивление средней ветви z = r + ĵ (х - х ) = 0 + ĵ ( 35 – 0 ) = ĵ 35;
сопротивление правой ветви z = ( r + r ) + ĵ [(х + х ) – ( х + х )] = ( 10 + 10 ) + ĵ [( 30 +40 ) – ( 15 + 40)] = 20 + ĵ 15.
1.3. Представим ЭДС Е и Е в комплексной форме, с учетом начальных фазовых углов
φ = + 90º и φ = + 135º:
Е = Е ( cos φ + ĵ sin φ ) = 40 (cos 90º + ĵ sin 90º ) = 40 ( 0 + ĵ1 ) = ĵ40;
Е = Е ( cos φ + ĵ sin φ ) = 60 (cos 135º + ĵ sin 135º ) = 60 ( - 0,707 + ĵ 0,797 ) = - 42,42 + ĵ42,42.
1.3. После расчета полных сопротивлений ветвей заменим промежуточную схему на рис. 2 рабочей на рис. 3.
На рабочей схеме полные сопротивления ветвей условно изображены прямоуголь-
никами z = 20 – ĵ5, z = ĵ 35 и z = 20 + ĵ 15.
2. Расчет электрической цепи методом контурных токов
1. Для удобства составления уравнений заменим схему на рис. 3 равнозначной
схемой на рис. 4. Последняя более удобна для изображения контурных токов I' и I''.
Направления контурных токов выбираем произвольно, например, для тока I' по
часовой стрелке, для тока I'' – против часовой стрелки.
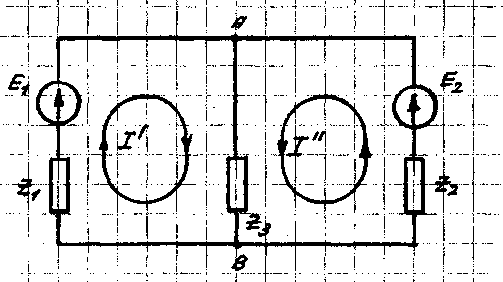
Рис. 4. Схема замещения с контурными токами
2. Применим 2-й закон Кирхгофа к контурам I и II
для контура I: Е = I' (z + z ) + I'' z ( 1 );
для контура II: Е = I'' ( z + z ) + I'z ( 2 ).
Найдем из уравнения ( 2 ) ток I'':
I'' = ( Е - I'z ) / ( z + z ) ( 3 )
4. подставим уравнение ( 3 ) в уравнение ( 1 )
Е = I' (z + z ) +( Е - I' z )* z / (z + z ) ( 4 )
в уравнении ( 4 ) освободимся от знаменателя
Е *(z + z ) = I' (z + z )*(z + z ) +( Е - I' z )* z = I' (z *z + z * z + z * z + z ) + Е * z - I' z = I' (z *z + z * z + z * z + z - z ) + Е * z ,
в скобках правой части уравнения рядом расположенные члены z и ( - z ) взаимноуничтожаются.
5. перенесем Е * z в левую часть уравнения ( с переменой знака )
Е *(z + z ) - Е * z = I' (z *z + z * z + z * z ), откуда
I' = I = [Е *(z + z ) - Е * z ] / [ (z *z + z * z + z * z )]=
= [ ĵ40 ( ĵ35 + 20 + ĵ15 ) – ( - 42,42 + ĵ42,42 )*( 20 + ĵ15 ) ] / [ ( 20 – ĵ5) (ĵ35 ) + ( 20 – ĵ5 )*
( 20 + ĵ15 ) + ĵ35( 20 + ĵ15 ) ] = [ ĵ 1400 + ĵ800 + ĵ 600 + 848,4 + ĵ636,3 – ĵ848,4 - ĵ 636,3 ] /
/ [ ĵ 700 - ĵ 175 + 400 + ĵ300 – ĵ100 - ĵ 75 + ĵ700 + ĵ525 ] =
= [ ( -1 )*1400 + ĵ800 – 600 + 848,4 + + ĵ636,3 - ĵ848,4 – ( - 1 )*636,3 ] / [ ĵ 700 – ( - 1 )*175 +
+ 400 + + ĵ300 – ĵ100 – ( - 1 ) 75 + ĵ700 + ĵ525 ] = ( - 515,3 + ĵ587,9 ) / ( 125 + ĵ1600 ) =
= ( - 515,3 + ĵ587,9 )* ( 125 - ĵ1600 ) / ( 125 + ĵ1600 )* ( 125 - ĵ1600 ) =
= ( - 64412,5 + ĵ 824480 + ĵ73487,5 - ĵ 940640 ) / ( 125 + 1600 ) =
= [- 64412,5 + ĵ 824480 + ĵ73487,5 – ( - 1 )*940640 ] / ( 15625 + 2560000 ) =
= [- 64412,5 + ĵ 824480 + ĵ73487,5 + 940640 ] / ( 2575625 ) = ( 876227,5 + ĵ897967,5 ) /
/ ( 2575625 ) = 0,34 + ĵ0,3486 ( 5 )
в приведенном выше расчете применялись известные из теории комплексных чисел соотношения и действия:
1. величина ĵ
=
(
-1 ) *
(
-1 ) = - 1; .
для освобождения знаменателя от комплексных чисел знаменатель умножают
на сопряженное число, т.е. на такое число, которое отличается от исходного знаком мни
мой части. В теории комплексных чисел произведение сопряженных чисел всегда дает действительное число:
( а + ĵ b )* ( а - ĵ b ) = а - ĵ аb + ĵ аb - ĵ b = а - ( - 1 )b = а + b .
В данном примере знаменатель ( 125 + ĵ 1600 ) умножался на сопряженное число
( 125 - ĵ 1600 ), что давало результат ( 125 + 1600 ). Одновременно с умножением на сопряженное число знаменателя надо умножать на это же число числитель – чтобы вели
чина дроби не изменилась.
В дальнейшем, с целью сокращения объема записи, промежуточные выкладки не приводятся.
8. подставим ( 5 ) в ( 3 ) :
I'' = I = ( Е - I' z ) / (z + z ) = [( - 42,42 + ĵ42,42 ) – ( 0,34 + ĵ0,3486 )*( 20 + ĵ15 )] /
/ ( ĵ35 + 20 + ĵ15 ) = … = 0,22 + ĵ0,968.
9. на основании 1-го закона Кирхгофа, ток через сопротивление z ( рис. 4 )
I = I + I = 0,34 + ĵ0,3486 + 0,22 + ĵ0,968 = 0,56 + ĵ 1,316.
10. окончательно:
ток левой ветви I = 0,34 + ĵ0,3486;
ток средней ветви I = 0,22 + ĵ0,968;
ток правой ветви I = 0,56 + ĵ 1,316.