
- •Раздел 1. Осмысление математического аппарата для решения экономических задач
- •1.1. Экстремум функции нескольких переменных
- •1.2. Достаточный признак существования экстремума
- •1.3. Условный экстремум
- •1.4. Метод наименьших квадратов
- •1.5. Правила составления систем стандартных уравнений
- •1.6.2. Биквадратная функция
- •1.6.3. Кубическая функция
- •1.6.4. Обратно пропорциональная функция
- •1.6.5. Дробно-линейная функция
- •1.6.6. Дробно-рациональные функции
- •1.6.7. Степенная функция
- •1.6.7.1. Степенная функция с натуральным показателем
- •1.6.7.2. Степенная функция с целым отрицательным показателем
- •1.6.7.3. Степенная функция с дробным показателем
- •1.6.8. Показательная функция
- •1.6.9. Логарифмическая функция
- •1.7. Асимптоты с привлекательными функциями для измерения экономических процессов (показателей)
- •1.8. Некоторые обобщения
- •1) Сумма квадратов отклонений
- •2) Сумма модулей отклонений
- •1.9. Вопросы для самоконтроля
- •1.10. Тренировочные задачи
- •1.11. Тест к разделу 1
- •Раздел 2. Эконометрические модели
- •2.1. Измеряющие (регрессионные) модели и корреляция
- •2.1.1. Частная корреляция
- •2.2. Имитирование (интерпретация) регрессионных моделей
- •2.3. Эконометрические модели спроса
- •2.4. Эконометрические модели ценообразования
1.8. Некоторые обобщения
Рассмотрим, например, функцию потребления:

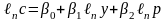 ,
,
где с - потребление некоторых пищевых продуктов на душу населения в некотором году;
y - реальные доходы на душу населения;
p - индекс цен на этот продукт;
0, 1, 2 - константы.
Это уравнение описывает (в среднем) поведение потребителя по отношению к покупке данного пищевого продукта в зависимости от уровня цен и реального душевого дохода.
Закон поведения будет определен, как только мы найдем значения коэффициентов 0, 1, 2. Соответственно задача эконометрики - определить (оценить) эти коэффициенты. Но это не единственная задача. Можно задать много других вопросов, например, нет ли переменных, которые следовало бы дополнительно включить в уравнение? Не следует ли исключить из уравнения некоторые переменные? Насколько адекватно измерены наши данные? Верно ли, что модель линейная? и т.д. Эконометрика рассматривает все эти вопросы в полном объеме. При этом в зависимости от конкретных обстоятельств и ситуации могут формироваться различные модели: однофакторные, двухфакторные и многофакторные. Формируются они, главным образом, на основе классических регрессионных моделей.
Пример:
пусть
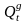 - спрос на товар в момент t,
- спрос на товар в момент t,
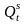 - предложение товара в момент t,
pt
- цена товара в момент времени t,
yt
- доход в момент времени t.
В этом случае уравнение спроса, предложения
имеет вид:
- предложение товара в момент t,
pt
- цена товара в момент времени t,
yt
- доход в момент времени t.
В этом случае уравнение спроса, предложения
имеет вид:
1.
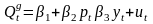 (уравнение спроса).
(уравнение спроса).
2.
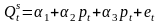 (уравнение предложения).
(уравнение предложения).
Рассмотрим модель парной регрессии. Пусть у нас есть набор значений двух переменных: xt, yt, t = 1,2,..., n. Предположим, что задачей является подобрать функцию y = f(x) из параметрического семейства функций f(x, ), наилучшим образом описывающую зависимость y от x. Поиск функции данного типа означает практически, что нужно выбрать "наилучшее" значение параметра .
В качестве меры отклонения функции f (x, ) от набора наблюдений можно взять:
- сумму квадратов отклонений, т.е.
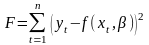 ;
;
- сумму модулей отклонений, т.е.
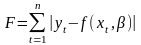 ;
;
- или в общем случае
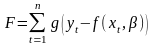 ,
,
где
g
- "мера", с которой отклонение
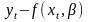 входит в функцию F.
входит в функцию F.
Достоинства и недостатки перечисленных функционалов:
1) Сумма квадратов отклонений
плюсы:
- легкость вычислительной процедуры;
- хорошие статистические свойства, простота математических выводов, тщательная проверка различных статистических гипотез.
минусы:
- чувствительность к выбросам (outliers).
2) Сумма модулей отклонений
плюсы:
- нечувствительность к выбросам.
минусы:
- сложность вычислительной процедуры;
- возможность больших отклонений между фактическими и проектными функциями;
- неоднозначность значений параметров и т.д.
Это всего лишь исходные предпосылки для изучения курса. Чувствуется, что для овладения эконометрическими методами необходимо:
а) иметь представление об экономике и экономическом образе мышления;
б) знать в достаточной степени теорию функционального анализа, т.е. высшую математику с практических позиций;
в) уметь ставить и представлять ход поведения экономических процессов.
1.9. Вопросы для самоконтроля
1. Дайте определение максимума, минимума функции в точке М0 (х0, у0).
2. Сформулируйте необходимые условия для существования экстремума функции.
3. Сформулируйте, при каких обстоятельствах достигает функция максимума, минимума, при каких обстоятельствах остается вопрос открытым и требуются дополнительные исследования.
4. В чем экономический смысл уравнения связи? Как она выбирается?
5. При каких обстоятельствах используется метод неопределенных множителей Лагранжа?
6. В чем экономический смысл метода наименьших квадратов?
7. Каким образом определяются параметры системы? Например, а, b, c для функции
у
=
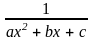 .
.
8. В чем экономический смысл величины ε1, ε2, …, εn в системе МНК? Всегда ли они имеют место?
9. Сформулируйте правило составления системы стандартных уравнений.
10. Составьте систему стандартных уравнений для следующих функций:
1.
у = а -
bx; 2.
y
=
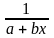 ;
;
3.
y
= a
+ bx
+ c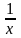 ; 4.
y
=
; 4.
y
=
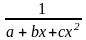 ;
;
5.
y =
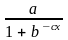 ; 6.
y = a · bx;
; 6.
y = a · bx;
7. y = a · xb; 8. y = a + a1x1 + a2x2.
11. Прокомментируйте наиболее привлекательные функции для исследования спроса, предложения, выпуска продукции.
12. Дайте оценку функции у = ℓоg х для исследования спроса, выпуска продукции.
13. Сформулируйте общую схему исследования функции и построения их графиков.
