1.5. Правила составления систем стандартных уравнений

Существует определенное правило составления системы стандартных уравнений:

1. Записывается исходное уравнение:

y = a + bx.

2. Перемножаются все члены уравнения на коэффициент при первом неизвестном и суммируются. Одновременно первый член (а) умножается на (n), т.е. на число наблюдений:

.

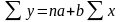3. Далее в системе перемножаются все члены уравнения на коэффициент при втором неизвестном и также суммируются:

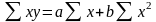и т.д.

Итак, система стандартных уравнений для функции у = а + bx имеет вид:

Для параболы второй степени у = а + bх + сх² система стандартных уравнений имеет вид:

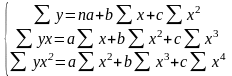
Для параболы третьей степени у = а + bх + сх² + dx³:

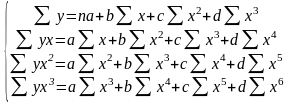
Для функции у = а + 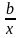система стандартных уравнений имеет вид:

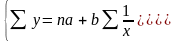
Для функции у = 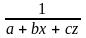система стандартных уравнений записывается следующим образом:

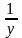= а + bx + cz

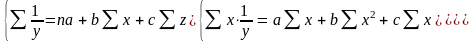
Для функции у = а + а₁х₁ + а₂х₂ + а₃х₃ система стандартных уравнений имеет вид:

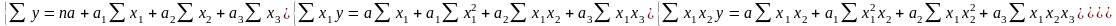
1.6. Наиболее привлекательные функции для измерения

экономических процессов (спроса, выпуска продукции,

ценообразования и других)

Для количественной оценки технико-экономических показателей, в частности спроса, предложения (выпуска продукции) и других возможно применение не только линейных, но и различных более усложненных функций.

1.6.1. Квадратичная функция

Зависимость между спросом и насыщенностью потребительского рынка вполне может выражаться функцией вида:

y = aх² + bx + с,

где х - насыщенность рынка;

у - спрос;

а, b, с - параметры системы.

Предположим, что b = 0, с = 0. Тогда функция примет вид:

y = ax².

График, последней функции в зависимости от величины коэффициентов а - принимает вид

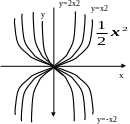
Рис. 2

Осуществим преобразования функции:

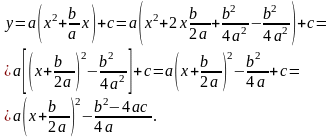
Итак,

Первая часть равенства есть сумма двух слагаемых, из которых 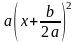зависит от переменной х, 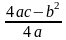не зависит от х, следовательно, имеет постоянное значение.

Чтобы получить график функции 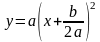, имея график у = ах², достаточно сдвинуть график у = ах² вдоль оси абсцисс на отрезок, равный 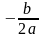, а затем достаточно произвести перенос вдоль оси ординат на величину .

Т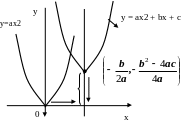 аким образом, чтобы получить график функции у = ах² + bx + c надо сдвинуть график у = ах² сначала вдоль оси абсцисс на отрезок , а затем вдоль оси ординат на . На рис. 3 показаны графики функции у = ах² + bx + c:

Рис. 3

1.6.2. Биквадратная функция

Функция вида

у = ах⁴ + bx² + c (а ≠ 0)

называется биквадратной.

После преобразования получим:

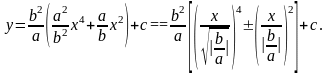
Если b ≠ 0, то график функции получается либо из графика функции у = х⁴ + х², либо из графика у = х⁴ - х².

График функции у = х⁴ + х², есть сумма графиков функции у = х⁴, у = х². На рис. 4 показан график данной функции:

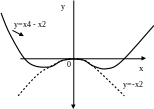
Рис. 4.

1.6.3. Кубическая функция

Функция вида у = ах³ + bх² + cx + d, где a ≠ 0, b, c и d - любые числа, называется кубической. В зависимости от конкретных обстоятельств данную функцию также возможно использовать для оценки основных технико-экономических показателей, и в том числе спроса, предложения, равновесных цен и других.

Функция у = х³. Если а = 1, b = c = d = 0. В данном случае график функции имеет вид:

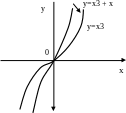
Рис. 5.