15. Теория двухъядерных молекул

238. Используя минимальный базис 1S-AO, покажите на основе вариационной теоремы, что в ионе возникает вместо Е_1s атома водорода два уровня (Е_g, E_u), из которых Е_g < Е_1s, а Е_u > Е_1s.

239. Найдите МО _g, _u иона и нормируйте их.

240. Найдите связь между координатами x, y, z декартовой системы, начало которой расположено на середине межъядерного расстояния двухъядерной молекулы, а ось OZ направлена вдоль линии ядер, и координатами , ,  эллиптической системы, в фокусах которой расположены эти ядра, если . Найдите области изменения координат , , .

Указание: Воспользуйтесь рисунком “Декартова и эллиптическая системы координат.

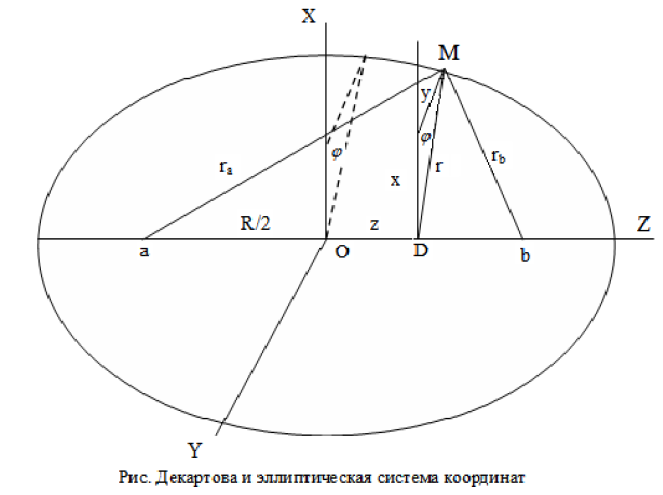
Для решения необходимо найти зависимости x = x (, ,  ), y = y (, ,  ),

z = z (, ,  ). Пусть плоскость эллипса наклонена к плоскости листа бумаги под углом . Спроецируем точку М эллипса на ось Z (точка D). Из рисунка видно, что x = r cos; y = r sin . Из MaD и MDb имеем:

r_a² = (z + R/2)² + r²; r_b² = (z - R/2)² + r². (1)

По условию

r_a² = R²(² + ²)/4; r_b² = R² (² - ²)/4 . (2)

Поочерёдно складывая и вычитая сначала равенства (1), а затем (2), приравнивая правые части равенств, соответственно действиям, найдём:

x = cos ; y = sin ; z = .

241. Пользуясь тем, что , постройте зависимость _g(R), _u(R) от R. Покажите, что в точке R/2 _u(R) имеет узел, а _g(R) узла не имеет.

242. Найдите коэффициенты Ламэ h_, h_v, h_ для эллиптической системы координат, если

h_q = , где q = , , ,

x = cos ; y = sin ; z = .

Ответ:

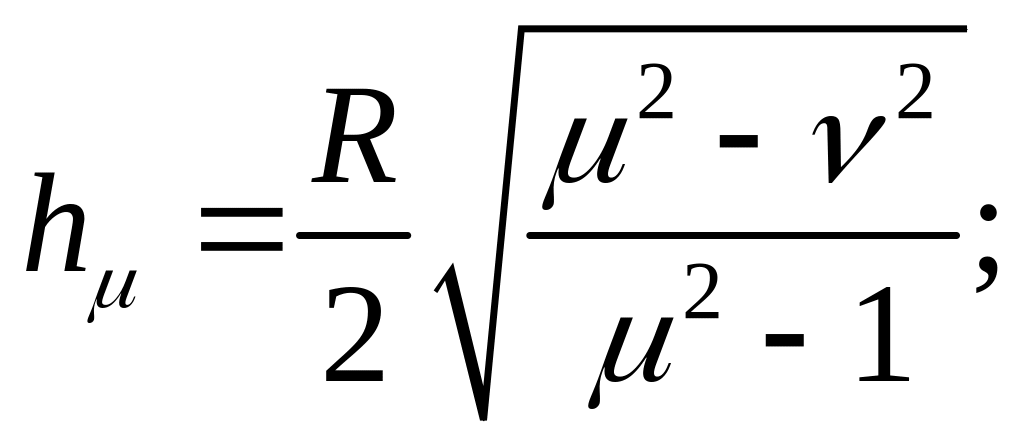
243. Найдите коэффициенты Ламэ h_r, h_z и h_ (см. №242) в цилиндрической системе координат, ось ОZ которой направлена вдоль линии, соединяющий ядра в двухъядерной молекуле, а начало координат находится на ядре а:

.

244. Найдите элемент объема в эллиптической системе координат:

.

Ответ: dV=(R³/8) (μ²-ν²) dμdνdφ; -1 1; 0

245. Найдите элемент объема в цилиндрической системе координат:

.

246. Найдите элемент объема в сферической системе координат:

.

247. Получите выражение для оператора Лапласа в сферической системе координат.

248. Получите выражение для оператора Лапласа в цилиндрической системе координат.

249. Получите выражение для оператора в сферической системе координат.

250. Получите выражение для оператора в цилиндрической системе координат.

251. Получите выражение для гамильтониана иона в цилиндрической системе координат, начало которой помещено в одно из ядер.

252. Покажите, что в двухъядерной молекуле = 0, т.е. гамильтониан коммутирует с оператором проекции углового момента на ось OZ.

253. Найдите собственные значения оператора в ионе . Покажите, что состояние электрона в ионе можно классифицировать по осевому квантовому числу, определяющему проекцию углового момента электрона ,  = 0, 1, 2...

254. Покажите, что в кулоновском приближении МО могут быть всегда выбраны в действительной форме.

255. Покажите, что МО гомоядерных двухатомных молекул можно классифицировать на четные (_g) и нечетные (_u).

256. Покажите, что в двухъядерной молекуле состояние электрона с осевым квантовым числом 0 двукратно вырождено.

257. Покажите, что если гамильтониан молекулы действителен, волновые функции (и в частности -МО) можно выбрать действительными.

258. Покажите, что если молекула обладает симметрией, то состояния ее в общем случае вырождены.

259. Постройте угловую зависимость - и -молекулярных орбиталей в ионе Н₂⁺ в плоскости Z=const.

260. Постройте угловую зависимость -орбиталей гомоядерной двухатомной молекулы в плоскости Z=0, преобразовав их предварительно к действительной форме.

261. Покажите, что “разрыхляющая” МО “разрыхляет” электронное состояние сильнее, чем “связывающая” МО “связывает”.

262. Проанализируйте, какие из МО относятся к связывающим, а какие к антисвязывающим. Обобщите полученный результат.

263. Пользуясь угловыми зависимостями АО, постройте качественно вид - и - МО вдоль ОZ.

264. Покажите на примере двухъядерной молекулы, что можно выбрать приближенную модель состояний электронов, из которой следует, что внутренние электроны существенно не влияют на энергию связи в молекуле, а связь эта обусловлена валентными электронами атомов.

265. Найдите электронные конфигурации двухъядерных молекул Li₂ , Be₂ , B₂ , C₂ , N₂ , O₂ , F₂ , Ne₂ , а также ионов , .

266. Вычислите интеграл перекрывания между 1S_a- и 1S_b-АО в ионе при R=const. Вычисления выполните в эллиптической системе координат (см. №240).

;

Указание: Сделайте замену величин r_a и r_b через эллиптические координаты и после разделения переменных интегрируйте по частям.

Ответ: S=e^-R₀ (1+R₀+(R₀²/3)), где R₀ = R/a₀ .

267. Вычислите в эллиптической системе координат (см.№240) интеграл притяжения электрона:

, где .

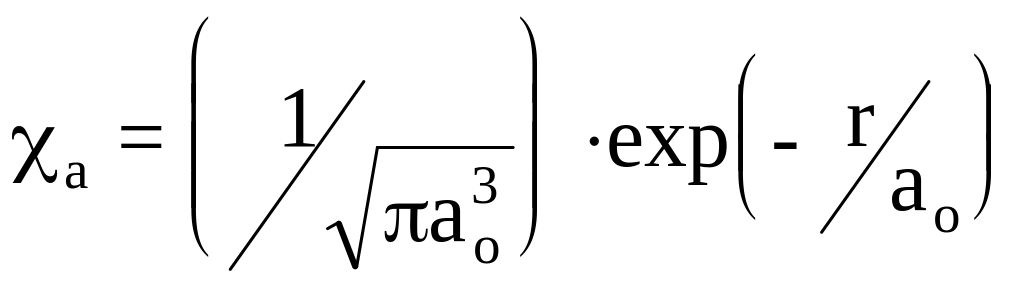Исследуйте поведение полученного интеграла на малых и больших расстояниях R между ядрами.

268. Найдите интеграл притяжения к ядру b: и исследуйте его как функцию от R, если .

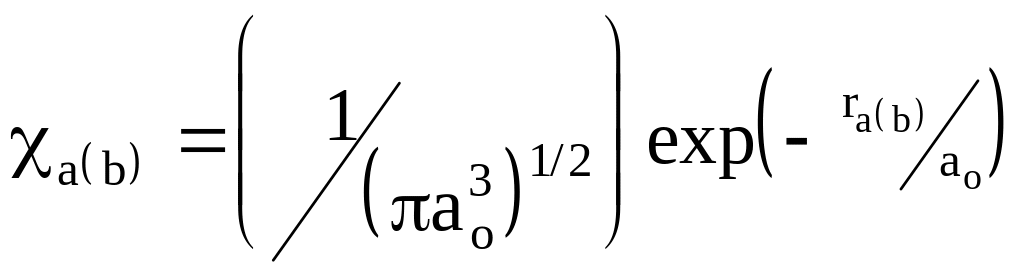269. Как возвести матрицу S в степень 1/2? Найдите симметрично ортогонализированные МО в ионе с помощью матрицы .

270. Покажите, что p-АО преобразуется как соответствующие компоненты радиус-вектора при преобразованиях координат.

271. Покажите, что S-АО инвариантны относительно поворотов декартовой системы координат.

272. Покажите, используя симметрию p-, p-АО, что интегралы типа ppsp0, ppps=0.

273. Найдите среднее значение кинетической энергии электрона в базисе 1S-AO в молекуле .

274. Объясните, почему у молекулы длина связи примерно в 4 раза больше длины связи Н₂, а соответствующая энергия связи в 4 раза меньше.

275. Функцией каких координат является интеграл ?

276. Постройте график S=S(R) зависимости интеграла перекрывания от R.

277. Постройте график зависимости интеграла задачи 267 от R . Сравните этот график с графиком функции .

278. Постройте график зависимости интеграла задачи 268 от R. Сравните этот график с графиком из задачи 277. Сделайте вывод о причинах понижения энергии электрона в ионе по сравнению с атомом Н.

16. -ЭЛЕКТРОННОЕ ПРИБЛИЖЕНИЕ

279. Что понимают под -МО многоядерных молекул? Для молекул какого строения имеет смысл введение -МО?

280. Покажите, что -МО планарных молекул антисимметричны относительно отражения в плоскости молекул.

281. Покажите, что для планарных молекул матрица эффективного гамильтониана F может быть представлена в блочном виде: , где элементы матриц нулевых блоков имеют вид: .

282. Для какого типа задач эффективно использование -электронного приближения?

283. Почему -МО многоядерных молекул, как правило, сильно делокализованы. Что означает делокализация -МО?