
- •1. Основные понятия теории вероятностей: событие (случайное, достоверное, невозможное, противоположное), совместные и несовместные события, равновозможные события.
- •2. Операции над событиями (сумма, произведение, разность).
- •3. Элементарное событие. Генеральная совокупность.
- •4. Классическое определение вероятности.
- •5. Свойства вероятности.
- •6. Геометрическая вероятность.
- •13. Формула Байеса
- •14. Схема Бернулли
- •15. Полиномиальная схема
- •16. Аксиоматическая теория вероятностей: вероятностное пространство, сигма-алгебра, случайная величина.
- •17. Дискретная случайная величина
- •20. Некоторые распределения дискретных случайных величин: биномиальное, геометрическое, гипергеометрическое.
- •21. Пуассоновское распределение, теорема Пуассона.
- •22. Некоторые распределения непрерывных случайных величин: равномерное на отрезке, показательное, нормальное, распределение Вейбулла.
- •23.Математическое ожидание для дискретных и непрерывных случайных величин.
- •24. Свойства математического ожидания.
- •25. Дисперсия для дискретных и непрерывных случайных величин.
- •27. Начальные центральные моменты для дискретных и непрерывных случайных величин.
- •28. Коэффициенты асимметрии и эксцесса.
- •29. Функции от дискретных и непрерывных случайных величин.
- •34. Корреляция, свойства корреляции.
- •35. Регрессия. Линейная регрессия.
- •36. Характеристическая функция, её свойства.
- •38. Теорема Чебышева
- •39. Закон больших чисел (теорема).
- •40. Центральная предельная теорема.
- •41. Теорема Ляпунова
- •42. Локальная теорема Муавра-Лапласа.
- •44. Теорема Берри-Эссеена.
- •45. Функция от многомерной случайной величины (на примере двумерных дискретных и непрерывных случайных величин).
- •46. Свертка и её свойства.
- •47. Выборка, вариационный ряд (дискретный и интервальный), ранжирование.
38. Теорема Чебышева
При достаточно больших n
для последовательности случайных
независимых величин
![]() таких что
таких что
![]() - положительное число, справедливо
неравенство:
- положительное число, справедливо
неравенство:

Док-во: Пусть
- независимые случайные величины,
рассмотрим
![]() -
случайная величина.
-
случайная величина.
![]() ,
,
![]()
Подставим
![]() в неравенство Чебышёва
,
тогда
в неравенство Чебышёва
,
тогда
![]()

т.к. по условию
![]()

т.к. для любого h>0
сколь угодно малого n:
![]()

39. Закон больших чисел (теорема).
Пусть
- независимые одинаково распределенные
случайные величины (имеют одинаковые
характеристики, если эти характеристики
существуют). Пусть существует
![]() ,
,
![]() ,
тогда для любого
справедливо:
,
тогда для любого
справедливо:

Док-во: Пусть
,
![]() ,
,
![]()
Подставим в неравенство Чебышёва , тогда
![]()
![]()
(**)
Замечание: Для выполнения закона больших чисел необходимым и достаточным условием является существование мат ожидания , более того существует последовательность независимых случайных величин, которые не имеют ни , ни , но при этом для них выполняется закон больших чисел.
Пусть - независимые одинаково распределенные случайные величины.
![]() -
случайная величина для которой выполняется
ЗБЧ.
-
случайная величина для которой выполняется
ЗБЧ.
Рассмотрим последовательность:
![]() .
Для этой последовательность не
гарантируется выполнение ЗБЧ для каждого
элементарного события w.
Тогда Пусть
.
Для этой последовательность не
гарантируется выполнение ЗБЧ для каждого
элементарного события w.
Тогда Пусть
![]() не
сходится к а}
не
сходится к а}
Если ЗБЧ выполняется при P(A)=0, то это усиленный ЗБЧ.
Теорема: (усиленный ЗБЧ)
Существование мат ожидания является
необходимым и достаточным условием
выполнения усиленного ЗБЧ для
последовательности независимых
одинаково-распределенных случайных
величин
постоянная, а в этом случае совпадает
с мат ожиданием
,
т.е. Пусть существует
- независимая случайная величина, пусть
существует
![]() выполняется усиленный ЗБЧ при этом
выполняется усиленный ЗБЧ при этом
![]() в
пределе (**).
в
пределе (**).
40. Центральная предельная теорема.
Пусть
- независимые одинаково распределенные
случайные величины, пусть существует
конченое
и![]() ,
тогда для любого
,
тогда для любого
![]()
 ,
где
,
где
![]() - функция стандартного нормального
распределения
- функция стандартного нормального
распределения
 ,
если обозначить
,
если обозначить
![]() ,
то нормальная случайная величина
,
то нормальная случайная величина

Док-во: т.к. непрерывная функция, то сходимость в каждой точке последовательности функции распределения случайной величины к является слабой сходимостью.
Тогда для доказательства можно воспользоваться теоремой непрерывности.
Теорема непрерывности: Последовательность
функция распределения
![]() слабо
сходится к некоторой
слабо
сходится к некоторой
![]() последовательность
характеристических функций
последовательность
характеристических функций
![]() сходится к характеристической функции
сходится к характеристической функции
![]() равномерно
на каждом отрезке
равномерно
на каждом отрезке
![]()
Пусть
![]() - характеристическая функция
- характеристическая функция
![]() =>
=>
![]() -
характеристическая функция
-
характеристическая функция
![]()
![]() по
свойству характеристической функции
по
свойству характеристической функции

Т.О.
 ,
по свойству характеристической функции
существуют
,
по свойству характеристической функции
существуют
![]() и
и
![]()
Тогда рассмотрим
 для этой функции можно построить ряд
Маклорена по степеням
для этой функции можно построить ряд
Маклорена по степеням
![]() до 2 числа включительно.
до 2 числа включительно.

![]()

![]()

![]()
=>

=>![]() -
характеристическая функция стандартного
нормального распределения.
-
характеристическая функция стандартного
нормального распределения.
Покажем, что
![]() ,
где
- характеристическая функция стандартного
нормального распределения
,
где
- характеристическая функция стандартного
нормального распределения
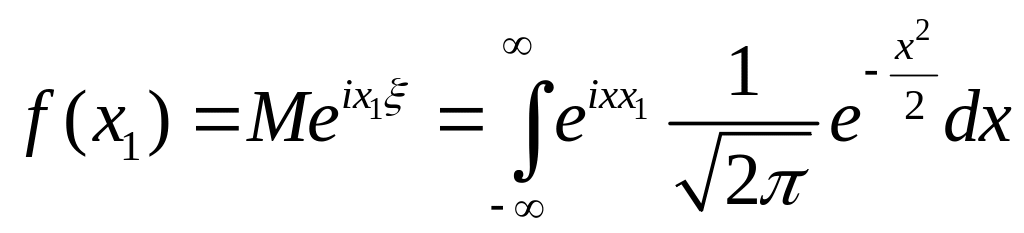
Пусть t = x1
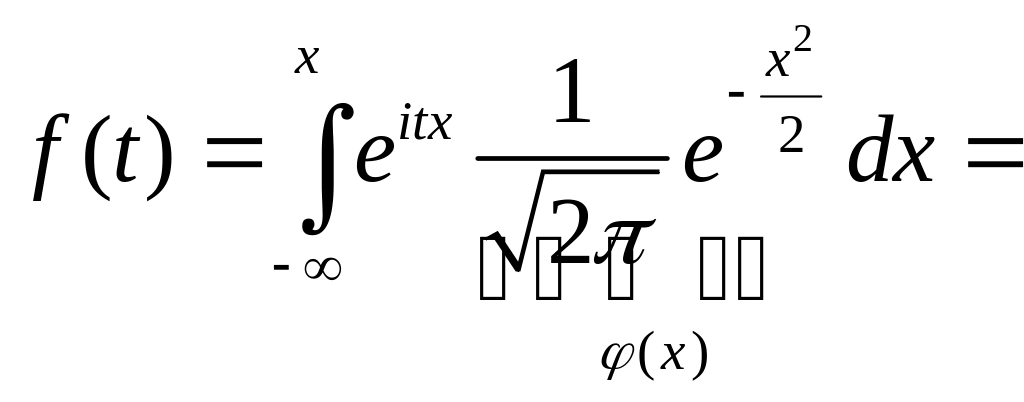
Замена: y = x – it

41. Теорема Ляпунова
Сумма независимых случайных величин
имеет распределение, которое с ростом
n приближается к
нормальному, если выполняются условия:
1)
![]() существую конечные
существую конечные
![]() и
и
![]() 2)
ни одна из случайных величин по своим
значениям не отличается от остальных
(т.е.
резко
не отличаются друг от друга).
2)
ни одна из случайных величин по своим
значениям не отличается от остальных
(т.е.
резко
не отличаются друг от друга).
Имеет большое практическое значение. Экспериментальным образом доказано, что уже при n>10 сумму независимых случайных величин можно рассматривать как нормально распределенную случайную величину.
Формулировка теоремы Ляпунова для дискретной случайной величины:
![]() ,
где
,
где
![]() - значения случайной величины x
(при n независимых
испытаниях).
- значения случайной величины x
(при n независимых
испытаниях).
Если случайная величина x
имеет конечное
![]() и
и
![]() ,то
распределение среднего арифметического
,то
распределение среднего арифметического
![]() вычисленного по наблюдавшимся значениям
случайной величины x,
проведенных в одинаковых условиях при
приближается
к нормальному.
вычисленного по наблюдавшимся значениям
случайной величины x,
проведенных в одинаковых условиях при
приближается
к нормальному.
![]() и
и
![]() ,
,
![]()

 ,
где
,
где
 ,
,

 - функция Лапласа.
- функция Лапласа.
