1.2. Интегрирующие и дифференцирующие цепи

В импульсных устройствах задающий генератор часто вырабатывает импульсы прямоугольной формы определенной длительности и ампли­туды, которые предназначаются для представления чисел и управления элементами вычислительных устройств, устройств обработки инфор­мации и др. Однако для правильного функционирования различных элементов в общем случае требуются импульсы вполне определенной формы, отличной от прямоугольной, имеющие заданные длительность и амплитуду. Вследствие этого возникает необходимость предвари­тельно преобразовывать импульсы задающего генератора. Характер преобразования может быть разным. Так, может потребоваться из­менить амплитуду или полярность, длительность задающих импульсов, осуществить их задержку во времени.

Преобразования в основном осуществляются с помощью линейных цепей — четырехполюсников, которые могут быть пассивными и актив­ными. В рассматриваемых цепях пассивные четырехполюсники не содер­жат в своем составе источников питания, активные используют энергию внутренних или внешних источников питания. С помощью линейных цепей осуществляются такие преобразования, как дифференцирование, интегрирование, укорочение импульсов, изменение амплитуды и поляр­ности, задержку импульсов во времени. Операции дифференцирования, интегрирования и укорочения импульсов выполняются соответственно дифференцирующими, интегрирующими и укорачивающими цепями. Изменение амплитуды и полярности импульса может производиться с помощью импульсного трансформатора, а задержка его во времени — линией задержки.

П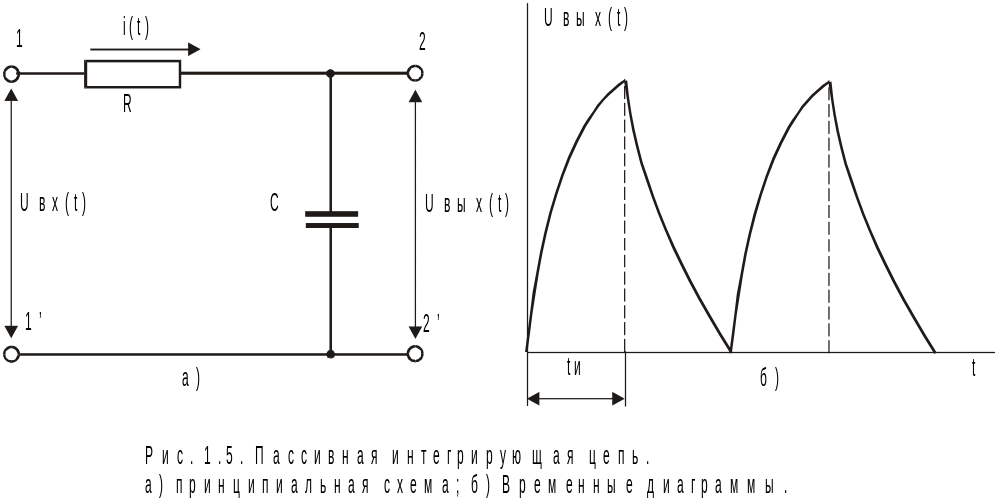 ассивная интегрирующая цепь. На рис.1.5,а приведена схема простейшей цепи (пассивного четырехполюсника), с помощью которой можно выполнить операцию интегрирования входного электрического сигнала, поданного на зажимы 1-1', если выходной сигнал снимать с зажимов 2-2'. Составим уравнение цепи для мгновенных значений токов и напряжений по второму закону Кирхгофа:

u_вх(t) = i(t)R + 1/C

Отсюда следует, что ток цепи будет изменяться по закону

i(t) = [u_вх(t)/R] - [1/(RC)]

Если выбрать постоянную времени т = RC достаточно большой, то вторым слагаемым в последнем уравнении можно пренебречь, тогда i(t) = u_вх(t)/R.

Напряжение на конденсаторе (на зажимах 2-2') будет равно

u_вых(t) = 1/C = 1/RC (1.1)

Из (1.1) видно, что цепь, приведенная на рис. 1.5,а, выполняет операцию интегрирования входного напряжения и умножения его на коэффициент пропорциональности, равный обратному значению постоянной времени цепи: 1/(RC) = 1/t. Временная диаграмма выходного напряжения интегрирующей цепи при подаче на вход последовательности прямоугольных импульсов показана на рис. 1.5,б.

П ассивная дифференцирующая цепь. С помощью цепи, схема которой приведена на рис. 1.6,а (пассивного четырехполюсника), можно выполнять операцию дифференцирования входного электрического сигнала, поданного на зажимы 1-1', если выходной сигнал снимать с зажимов 2-2'. Составим уравнение цепи для мгновенных значений тока и напряжения по второму закону Кирхгофа:

u_вх(t) = i(t)R + u_c(t) = i(t)R + 1/C

Если сопротивление R мало и членом i(t)R можно пренебречь, то ток в цепи i » C и выходное напряжение цепи, снимаемое с R,

u_вых(t) = i(t)R = RC (1.2)

Анализируя (1.2), можно видеть, что с помощью рассматриваемой цепи выполняют операции дифференцирования входного напряжения и умножения его на коэффициент пропорциональности, равный постоян­ной времени t = RC. Форма выходного напряжения дифференцирующей цепи при подаче на вход серии прямоугольных импульсов приведена на рис.1.6,б. В этом случае теоретически выходное напряжение должно представлять собой знакопеременные импульсы бесконечно большой амплитуды и малой (близкой к нулю) длительности. Однако вследствие различия свойств реальной и идеальной диф­ференцирующих цепей, а также конечной крутизны фронта импульса на выходе получают импульсы, амплитуда которых меньше амплитуды входного сигнала, а длительность их определяется как t_и= (3 ¸ 4) t = (3 ¸ 4)RС.

Пассивные интегрирующие и дифференцирующие цепи имеют сле­дующие недостатки: обе математические операции реализуются прибли­женно, с известными погрешностями. Приходится вводить корректи­рующие звенья, которые, в свою очередь, сильно снижают амплитуду выходного импульса, т. е. без промежуточного усиления сигналов практически невозможны n-кратные дифференцирование и интегриро­вание. Эти недостатки не свойственны активным дифференцирующему и интегрирующему устройствам. Одним из возможных способов реализации этих устройств является применение операционных усилителей

А ктивное дифференцирующее устройство. Схема такого устройства на операционном усилителе приведена на рис.1.7. Ко входу 1 подключен конденсатор С, а в цепь обратной связи включен резистор R_ос. Так как входное сопротивление чрезвычайно велико (R_вх ®µ), то входной ток обтекает схему по пути, указанному на рисунке. С другой сторо­ны, напряжение U_вхОУ в этом включении очень мало, так Кu ® µ , поэтому потенциал точки В схемы практически равен нулю. Следовательно, ток на входе

i(t) = -u_вых(t)/R_ос. (1.3)

Ток на выходе i(t) одновременно является зарядным током конденсатора С: dq = Cdu_вх{t), откуда

i(t) = С du_вх (t) / dt. (1.4)

Приравнивая левые части уравнений (1.3) и (1.4), можно написать -u_вых(t) /R_ос = C du_вх(t) /dt, откуда

u_вых(t) = - R_осC (1.5)

Таким образом, выходное напряжение операционного усилителя является произведением производной входного напряжения по времени, умноженной на постоянную времени t = R_осC.

А ктивное интегрирующее устройство. Схема интегрирующего устройства на операционном усилителе, приведенная на рис.1.8, отличается от дифференцирующего устройства рис.1.7 только тем, что конденсатор С и резистор R_oc (на рис.1.8-R₁) поменялись местами. по-прежнему R_вх ® µ и коэффициент усиления по напряжению К_u ® µ. Следовательно, в устройстве конденсатор С заряжается током i(t) = u_вх(t)/R₁. Так как напряжение на конденсаторе практически равно выходному напряжению (j_в = 0), а операционный усилитель изменяет фазу входного сигнала на угол p, имеем

u_вых(t) = - 1/R₁C . (1.6)

Таким образом, выходное напряжение активного интегрирующего устройства есть произведение определенного интеграла от входного напряжения по времени на коэффициент 1/т.