Статистическая физика

Введение: ОСНОВНЫЕ ПРИНЦИПЫ СТАТИСТИКИ

Статистика изучает закономерности, которым подчиняется поведение макроскопических тел, т.е. предметы статистики и термодинамики совпадают. Однако, в отличие от термодинамики, статистика исходит из модельных представлений о микроскопической структуре вещества. Ее задача состоит в том, чтобы устанавливать законы поведения макроскопических тел, используя законы движения частиц, из которых состоят эти тела.

Чтобы описать систему в рамках механики, нужно составить уравнения ее движения, число которых равно числу степенией свободы, и проинтегрировать их. Поскольку число степеней свободы макроскопической системы огромно, то сделать это практически невозможно.

На первый взгляд кажется, что с увеличением числа частиц свойства механической системы должны крайне усложняться и что в поведении макроскопического тела не будет даже следов закономерности. В действительности оказывается, что при большом числе частиц появляются качественно новые закономерности, не сводящиеся к механическим, которые называются статистическими. Задача статистики и состоит в установлении этих закономерностей. Поэтому статистика представляет обоснование термодинамики. Однако ее содержание не исчерпывается этим. Статистическая механика позволяет находить уравнение состояния и теплоемкость любой системы, т.е. решать задачи, которые в принципе неразрешимы в термодинамике. Наконец, статистика позволяет установить границы применимости законов термодинамики, предсказать их нарушения (флуктуации) и оценить масштаб этих нарушений. Для математической формулировки основной задачи статистической механики введем понятие фазового пространства, играющее важнейшую роль во всей статистике. Пусть имеется газ из N частиц (молекул). Между частицами происходят соударения, в результате которого устанавливается статистическое (термодинамическое) равновесие. Выделим из этой системы одну частицу и проследим как часто она будет попадать в заданный объём конфигурационного пространства V=xyz с координатами x, y, z и заданный объём импульсного пространства р=р_xр_yр_z с координатами р_x, р_y, р_z. Совокупность этих пространств называется фазовым пространством для одной частицы. При этом каждое состояние частицы изображается определенной точкой в фазовом пространстве. С течением времени микроскопическое состояние частицы изменяется, и фазовая точка описывает в фазовом пространстве кривую, называемую фазовой траекторией.

1. Основные понятия

1) Фазовое пространство – для одной частицы вводится 6-мерное пространство, его элементарный объём ,

dV – конфигурационное пространство ,

dp – пространство импульсов:

Так что, для одной частицы .

Состояние системы изображается точкой в фазовом пространстве, а изменение состояния во времени - движением точки вдоль линии, называемой фазовой траекторией.

Основной вопрос: нас будет интересовать вероятность , с которой выделенная частица попадает в элемент фазового пространства Г в процессе своего движения.

Вероятность определяется как отношение .

-- число частиц попавших в элемент фазового пространства, общее число частиц.

2) Функция распределения – вероятность пропорциональна элементу ФП:

,

где функция распределения – плотность распределения вероятности в ФП: вероятность, отнесённая к единичному элементу ФП.

4) Микросостояние системы – описание системы на микроуровне, когда задаются координаты и скорости всех частиц: . Иначе: известно какие частицы находятся в каждой фазовой ячейке.

5) Макросостояние системы – описание системы на макроуровне, когда задаются макропараметры (p, V, T, ).

Каждое макросостояние реализуется большим числом микросостояний.

Равновероятность микросостояний с энергией  в интервале энергий  – это утверждение относится к эргодической гипотезе.

6) Термодинамическая вероятность – число микросостояний системы, которыми реализуется одно ее макросостояние (>>1!!).

2. Микроканоническое распределение гиббса

       

Из последних положений вытекает, что все микросостояния данной системы равновероятны, вследствие чего статистический вес (число состояний, оно же и кратность вырождения!) оказывается пропорциональным вероятности макросостояния. Утверждение о равновероятности всех микросостояний лежит в основе статистической физики и носит название эргодической гипотезы.

Для замкнутой системы имеет место МИКРОКАНОНИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ГИББСА: Вероятность макросостояния пропорциональна его статистическому весу:

Фактически это следствие эргодической гипотезы: количество различных микросостояний, реализующих данное макросостояние системы, и есть статистический вес или термодинамическая вероятность макросостояния.

Замкнутая система находится с большей вероятностью в таком состоянии, которое имеет большую кратность вырождения.

Кратность вырождения – число микросостояний для заданного уровня энергии.

Доказательство того, что реальные системы являются эргодическими, - очень сложная и еще не решенная проблема.

3. Классические распределения

Будем рассматривать по отдельности:

1) вероятность нахождения частицы в элементе пространства импульсов . Соответствующая функция распределения называется ФР Максвелла:

2) вероятность нахождения частицы в элементе конфигурационного пространства . Соответствующая функция распределения называется ФР Больцмана: .

ФР Максвелла по проекции импульса:

Распадается на три функции по каждой проекции

Это распределение есть функция от проекции импульса и двух параметров: массаы и температуры.

Задание: исследовать поведение распределения от параметров: массы и температуры.

(m₁=4010^-27 кг; m₂=3010^-27 кг; Т₁=300 К; Т₂=600 К)

Заменой переменной ( ) получим распределение

Максвелла по проекции скорости:

ФР Максвелла по модулю скорости:

v

v

v₁ 1ё1

v₂ 1ё1

v_нв 1ё1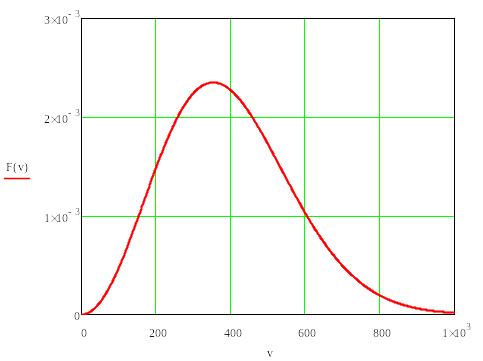

Свойства распределения Максвелла (они следуют из определения ):

Условие нормировки - площадь под функцией распределения есть вероятность того, что частица имеет скорость в интервале от 0 до  ( );

Доля частиц имеющих скорость в интервале от v₁ до v₂ - площадь под функцией распределения есть вероятность того, что частица имеет скорость в интервале от v₁ до v₂;

Для узкого интервала скоростей v можно записать .

Зная ФР можно вычислить среднее значение любой физической величины.

Характерные скорости

Среднее значение х-ой компоненты скорости:

Наиболее вероятная скорость – – скорость, при которой максимально:

Среднее значение модуля скорости

Среднеквадратичная скорость – связана со средней энергией молекулы

Используя выражение для наиболее вероятной скорости удобно записать ФР

; ;

Распределение по энергии (используется связь импульса и энергии )

(построить самостоятельно)

Средняя энергия молекул идеального газа поэтому необходимо вычислить интеграл

Замена переменной приводит к интегралу . Окончательно средняя энергия одноатомной молекулы

Следовательно, на одну степень свободы приходится – из классического закона равнораспределения энергии по степеням свободы.

2) вероятность нахождения частицы в элементе конфигурационного пространства .

Соответствующая функция распределения называется ФР Больцмана: .

Рассмотрим идеальный газ в силовом поле с потенциальной энергией, зависящей от координат

Вероятность попадания молекулы в элемент конфигурационного пространства dV – есть распределение Больцмана

Т. е. вероятность нахождения молекулы в данном объёме зависит от её потенциальной энергии во внешнем поле сил (множитель С_Б – находится из условия нормировки).

Обычно используется не функция распределения , а концентрация , которая определяется формулой:

,

где - полное число микрочастиц в объеме системы.

Т.о. концентрация частиц в силовом поле

Это распределение известно как барометрическая формула.

изобразим бесконечно малый выделенный объем газа , находящийся в равновесии. Снизу на этот выделенный объем газа воздействует давление , а сверху - соответственно давление . Условие механического равновесия для объема газа запишется в виде:

или

,

где: - плотность газа, - ускорение свободного падения, - масса одной молекулы газа.

Из МКТ и плотность газа ,
и уравнение для давления газа: .
Интегрирование приводит к зависимости давления от высоты , Или через молярную массу

.

Эта зависимость носит название барометрической формулы. Она, в частности, позволяет рассчитывать зависимость давления атмосферы от высоты в случае, если температура атмосферы постоянна, а гравитационное поле - однородно. Для реальной атмосферы Земли на высотах примерно до 10 км её температура уменьшается в среднем на 6 К на 1 км подъема. Далее до высот порядка 20 км температура остается практически постоянной, а выше - постепенно возрастает до ~ 270 К на высоте около 55 км. На этой высоте давление атмосферы становится уже меньше 0,001 от атмосферного давления на уровне моря.

Для концентрации получим

,

что совпадает с более общим выражением для распределения Бльцмана.

Это распределение позволяет рассчитывать концентрацию газа, находящегося в равновесном состоянии во внешнем силовом поле. Причем это поле не должно быть обязательно гравитационным, а может иметь любое происхождение, в частности, быть электростатическим или полем сил инерции.

Пример. Ротор центрифуги вращается с угловой скоростью ω. Используя функцию распределения Больцмана, установить распределение концентрации n частиц массой m, находящихся в роторе центрифуги, как функцию расстояния r от оси вращения.

Потенциальная энергия центробежных сил

Анализ распределения Больцмана показывает, что концентрация молекул газа тем выше, чем меньше их потенциальная энергия. Кроме этого, с понижением температуры увеличивается отличие концентраций в точках с различными значениями потенциальной энергии молекул. А при стремлении температуры к абсолютному нулю, молекулы начинают скапливаться в месте, где их потенциальная энергия принимает наименьшее значение. Указанные особенности распределения Больцмана являются следствием теплового движения молекул, так как кинетическая энергия их поступательного движения в среднем равна и уменьшается пропорционально уменьшению температуры. А уменьшение кинетической энергии приводит к уменьшению количества молекул, способных преодолеть потенциальный порог, высота которого характеризуется потенциальной энергией.

Пример. Среднее значение координаты молекулы в однородном гравитационном поле:

.

Среднее значение потенциальной энергии молекул газа:

.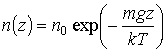