Table 4 to show number of combinations for Bob winning and number of combinations for Ann losing

Since Ann and Bob have their own private die and Ann throws two times and Bob throws twice as well, one after another, then these can be considered as Independent events. Since they are Independent events the formula for calculating the probability of Bob winning for each face (the highest number of two) of his die will be: . Where is the probability of Ann getting a losing combination and then it will e multiplied by which is a probability of Bob getting winning combination. And finally they will be added up to find probability that Bob wins:

Therefore the probability of Ann winning is:

The pattern for the number of possible combinations Ann has to get in order to lose was spotted from the previous cases examined. Basically the number on the face of the dice that happens to roll is and number of the throws Ann makes is . Therefore an expression for Ann getting any number on the face of the dice in number of rolls will be .

For Bob, however, it is different than to Ann since the condition (Ann wins if her score is higher than Bob’s and Bob wins if his score is higher or the same as Ann’s) is given in the problem.

Total number of possible outcomes is the denominator- and now the numerator has to be derived in order to get full satisfactory general equation which is basically the possible total number of ways when Bob wins for different values of or in other words Ann loses.

Firstly I need to find the part of the equation that represents Bob getting rolls of starting from number of rolls. It will be achieved by examining Bob getting maximum roll of and him having rolls. While doing it, two facts have to be considered: the biggest possible number of rolls of cannot be bigger than . So, for , there is only one possible way Bob gets rolls of . And secondly the order of the rolls has no impact on the number of the rolls of . Since I dealt with an easy part I will move onto the harder bit where the values of are in the range:

As I said earlier I have to look at it starting from rolls of . So, getting only 1 roll of , the number of ways can be represented as .

Because having to roll a number , the number happens to be at least once in every single possible combination. But only once for each value of there will be a combination that will contain only the values of (i.e for Bob throwing a die twice and rolling as 2, it will be (2,2)) that we are making the combinations for. Therefore it has to be in order to disregard this “only values of combination”

In this case the roll of could happen for any number of rolls. To get the part for representing the switching of the numbers around to get number of different possible rearrangements I am going to use Binomial Coefficients formula where will represent and will represent . Therefore for this particular case it will be , it can be simplified to just . It gives me, therefore, the part of the formula for this particular case where Bob is getting rolls of starting for . It is therefore .

Hence, having a formula derived for rolls, I am going to state the general formula for , where can be infinite:

Now to apply it for my case the summation is going to be involved in order to get the general formula for Bob having maximum roll of with rolls.

Now, since I have 2 important parts I put general formula together with some little modifications to add. Now I am going to put it together in order to calculate the number of times that Bob wins:

The above equation as was mentioned before starting deriving the general formula is the numerator. The reason there is is that there is only one possible way Bob gets rolls of , since .

Now in order to make it a probability the denominator will be attached:

The general equation is probability for Bob winning(Ann losing) and Bob losing(Ann winning) is:

Since I’ve found the formula I am going to test it by comparing the results I’ve found manually:

So the probability when each of them threw a die once only is:

P(Bob wins) found manually=

P(Ann wins) found manually=

The probability when Bob throws a die once and Ann throws hers twice:

P(Bob wins) found manually=

P(Ann wins) found manually=

The probability when Bob throws a die twice so as Ann:

P(Bob wins) found manually=

P(Ann wins) found manually=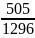

Since the results, found using the formula derived, match the results, that were found manually using tables, are the same, the general formula to find probability of Bob winning is correct and can be used for any other case where number of throws of each Bob and Ann can range from 1 to infinity.

Considering a dice game in any Casino by a common person it might seem to him that the most simplest case for both a player and the casino is to play one throw each. I am going to investigate what is the most appropriate payout is to be done by the “Glorious” in order to have as highest profit margins as possible however at the same time satisfies a player’s possible expectations, that are sensible, on the payout.

• “The Glorius” is planning on making the charge of the game(X) to be $5.

• Y is the payout by the casino to a player in case of winning.

In order to calculate a payout by the casino in case a player wins I at first have to look at the case of a fair game where nor player neither casino makes nor profit nor loss if multiple games played. It can be portrayed through the formula of an expected value:

In the case of a fair game

Therefore Y can be found by rearranging the formula and substituting the values into the equation:

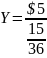
$12 will be paid to a player if he wins however no profit will be generated by the casino. At the end of the day any casino is a business which primary objective is not to play fair but to generate profit. However it can’t be done in such a manner so a player might feel like he is being fooled. To make sure that it doesn’t happen but the profit is still generated at a good and stable rate, a sensible decision for “The Glorious” may be to drop down the payout by $2 which will result in Y=$10(not a fair game any more) meaning that the profit margin is $2.

To make it easier for casino’s accountants and the financial department, profit margin as a percentage will be calculated by making a relationship between the profit and the payout from the fair game:

There is a possibility that Casino may decide to make its percentage profit margin to 1 significant figure, which means they may not stick to 16.7% but instead make it 20%. It means that payout will have to be not $10 but $9.6