
- •Сейсморазведка, III курс, 2011-12 уч. Год определение скоростей в сейсморазведке Определение скоростей в образцах пород
- •Определение скоростей по данным скважинных исследований
- •Определение скоростей по полевым материалам
- •Определение vогт с помощью рна скоростей
- •Определение Vэф по годографам отраженных и преломленных волн
- •Способ взаимных точек
- •Факторы, влияющие на точность определения скорости
- •Влияние случайных погрешностей измерения времени
- •Влияние кривизны отражающей границы
- •Влияние промежуточных границ
- •Влияние локальных неоднородностей в разрезе
- •Построение одномерной скоростной модели Vэф
Факторы, влияющие на точность определения скорости
Можно выделить следующие основные факторы:
Способ (алгоритм) определения Vэф. (Этот фактор частично рассматривался при оценке точности определения скорости).
Случайные ошибки измерения времени.
Наклон и кривизна отражающей границы.
Влияние вышележащих промежуточных границ.
Степень латеральной неоднородности среды
Влияние случайных погрешностей измерения времени
Дифференцируя выражения для Vэф в рассмотренных алгоритмах по параметру t найдем относительную среднеквадратическую погрешность (Vэф / Vэф):
![]() =
=
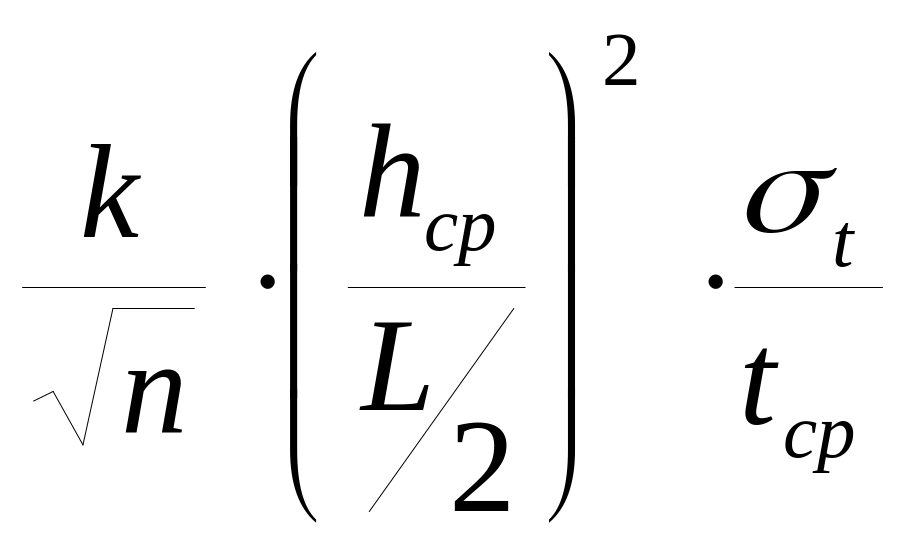
где tср – среднее время по годографу,
hср = (Vэф tср) / 2 – средний путь пробега волны до отражающей границы,
L / 2 – длина участка границы, освещаемого на одной сейсмограмме (L – длина расста- новки сейсмоприемников),
n – число пар точек, используемых на исходных годографах,
t – среднеквадратическая погрешность определения времени (обычно – 0.003 – 0,004 с),
k – коэффициент, зависящий от способа определения Vэф и числа n (при n >> 1 k 9.6).
Выводы:
При равных значениях t все способы практически равноточны.
t зависит от способа определения Vэф (при применении алгоритмов, использующих встречные годографы, уменьшается влияние наклона границ и неоднородностей ВЧР)
Относительная среднеквадратическая погрешность (Vэф / Vэф) зависит от отношения (L / h) – при “длинных” годографах она меньше, что справедливо для любого способа определения Vэф.
Влияние кривизны отражающей границы
Все рассмотренные ранее уравнения годографов были получены в предположении о плоской отражающей границе, Соответственно, это же предполагают и полученные на их основе выражения дляVэф.
Исследования (Пузырев Н.Н., 1959 г) показали, что степень искажения Vэф зависит от соотношения радиуса кривизны границы (R, при выпуклой границе R > 0, при вогнутой – R < 0) и глубины ее залегания (H). Для систем наблюдения с длиной расстановки L << R погрешность определения скорости (Vэффективная / Vистинная) приближенно выражается следующими соотношениями:
 =
=
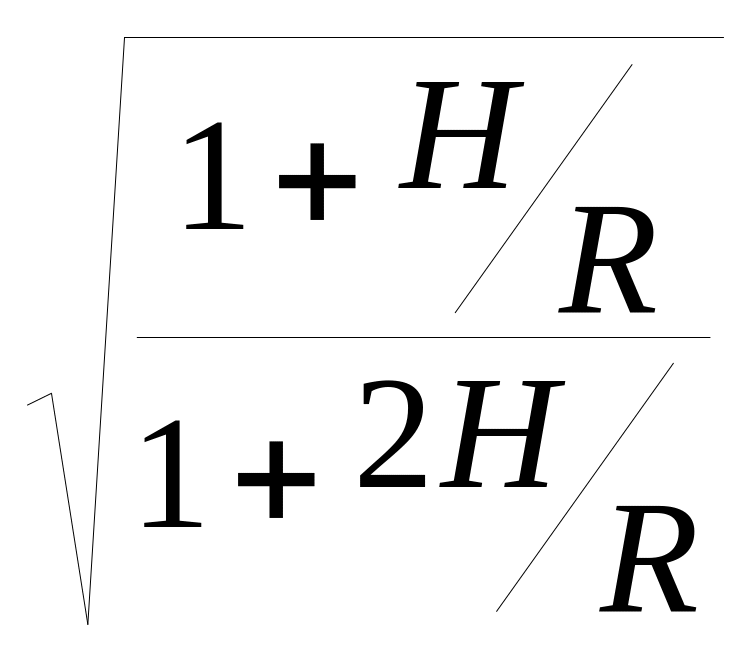 – для одиночных годографов;
– для одиночных годографов;=
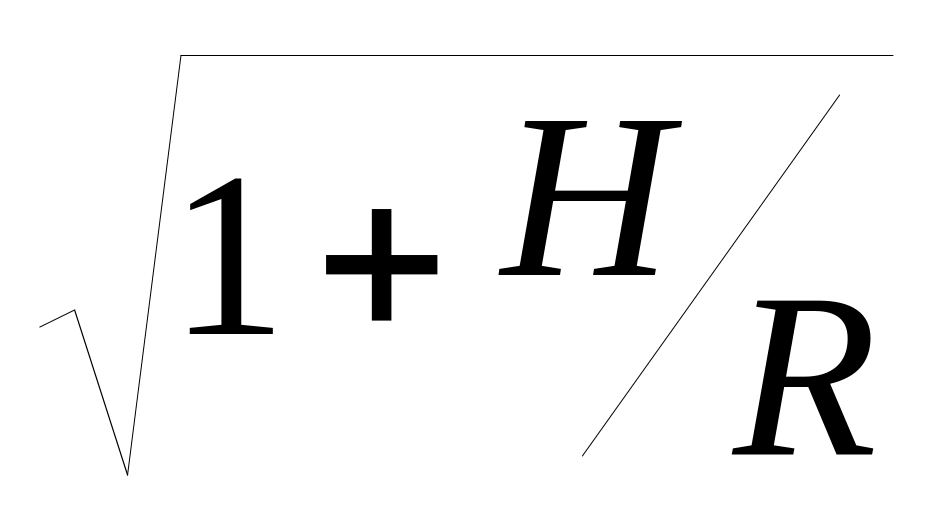 – для встречных годографов
(предполагается,
что центр кривизны нахо
дится между пунктами
возбуждения).
– для встречных годографов
(предполагается,
что центр кривизны нахо
дится между пунктами
возбуждения).
![]() .
.
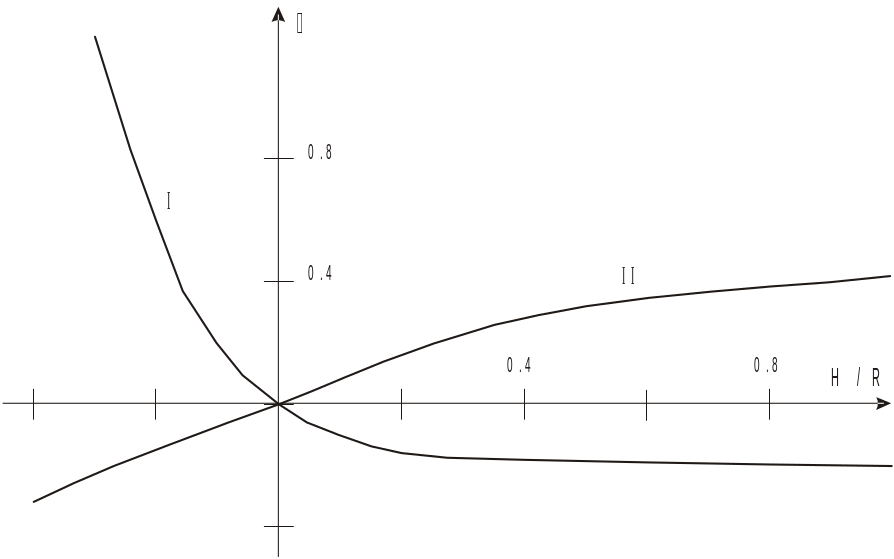
Характер зависимости относительной погрешности от вида используемых годографов и относительной глубины показан на приведенном графике, где кривая I соответствует одиночным годографам, а кривая II – встречным.
Влияние промежуточных границ
(см. также Гурвич И.И., Боганик Г.Н. Сейсмическая разведка, 1980г. §35, раздел 4, стр. 431-436)
Пусть имеется горизонтально-слоистая среда, в которой отсутствуют латеральные изменения пластовых скоростей, т.е. скорость в i-том слое Vпласт(i) = const (x,y) = Vi.
Уравнение годографа отраженной волны для двуслойной среды можно записать как:
V2t2 = 4h2 + l2 откуда следует l2 = V2t2 4h2 (6)
Кажущаяся скорость по определению V*
=
![]() .
Дифференцируем выражение (6) по параметру
t: 2
=
2
.
Дифференцируем выражение (6) по параметру
t: 2
=
2![]() .
Тогда V2 =
.
Тогда V2 =
![]() или V = Vэф
=
или V = Vэф
=
![]() (7)
(7)
Для m-слойного разреза можно записать систему параметрических уравнений:
l = 2![]() =
2
=
2![]() =
2
=
2
t = 2![]() =
2
=
2
Согласно закону Снеллиуса
![]() =
=![]() =
=![]() =
p, где р – параметр
луча, инвариантный по отношению к слою,
в котором распространяется волна, и
зависящий только от начального угла
луча 1.
Тогда:
=
p, где р – параметр
луча, инвариантный по отношению к слою,
в котором распространяется волна, и
зависящий только от начального угла
луча 1.
Тогда:
l = 2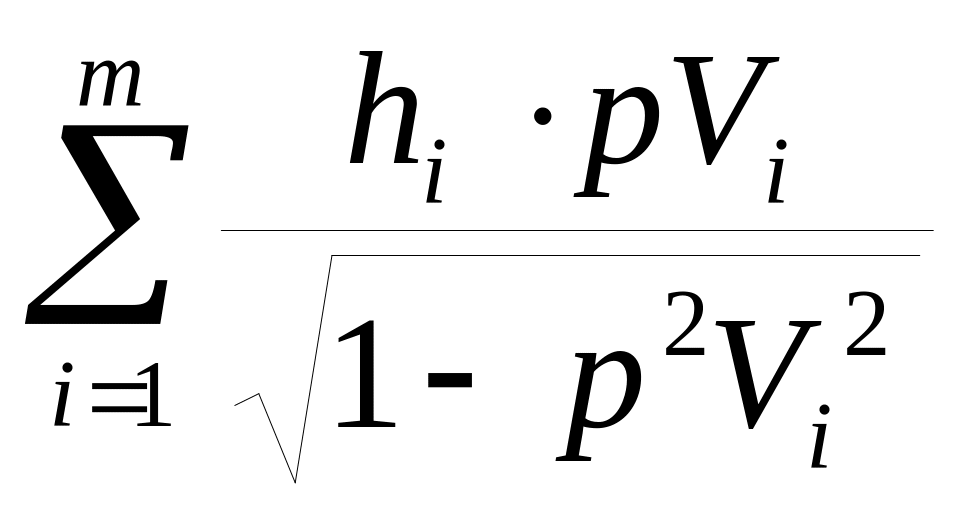
(8)
t = 2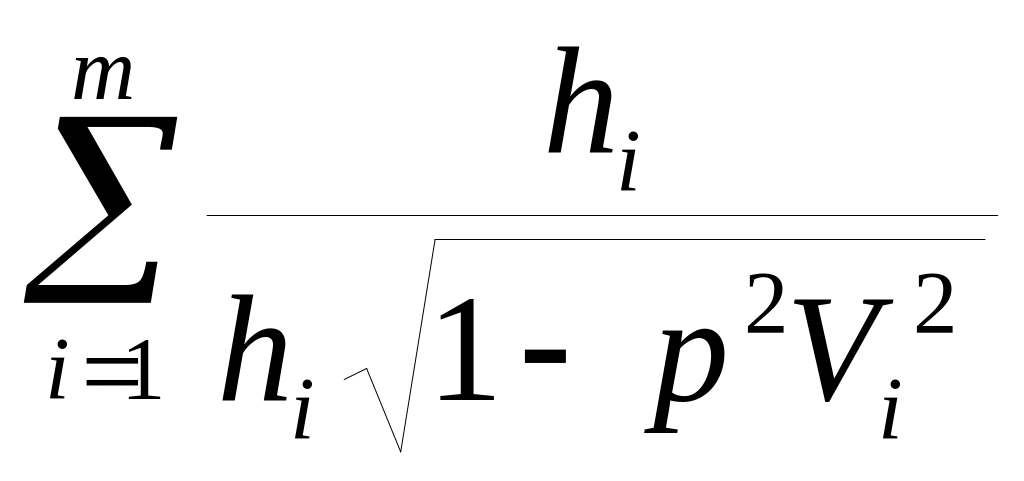
Подставим выражения для l и t из (8) в равенство (7) с учетом того, что p = :
Vэф =
![]()
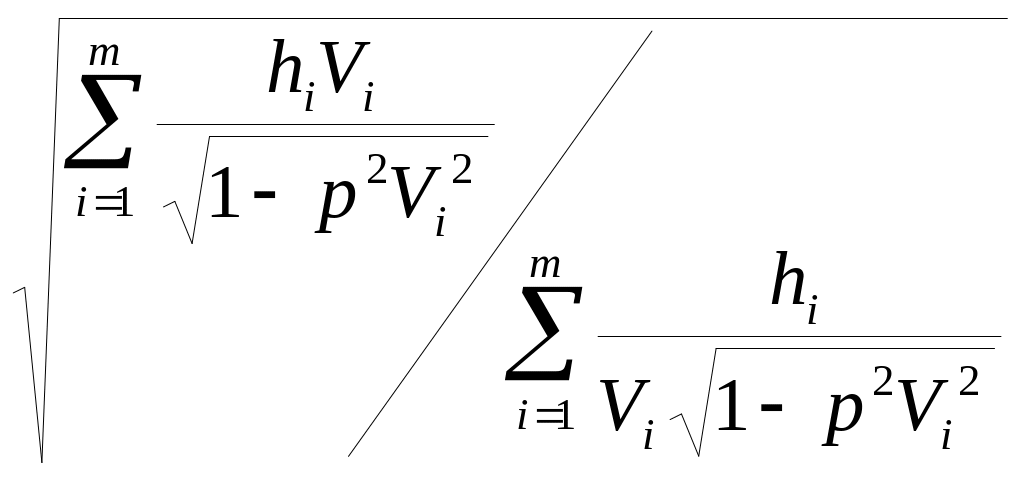 (9)
(9)
При сокращении используемой длины
годографа (l
0) параметр p
0 эффективная скорость стремиться к
предельной эффективной скорости (Vе
=![]() )
)
l 0
Полагая в выражении (9) p = 0, получим:
Ve
=
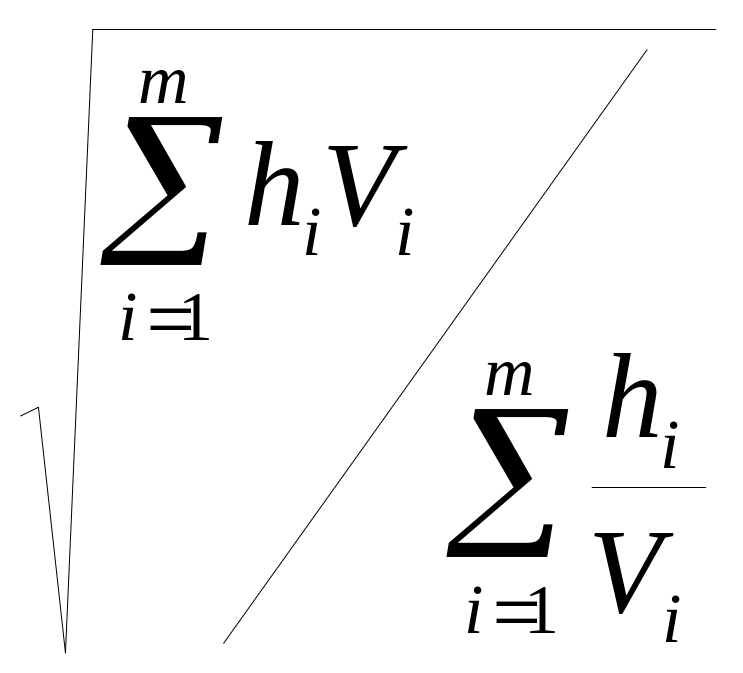 =
=
 ,
где ti
=
,
где ti
=
![]()
(сравните с выражением для средней скорости до m-ной границы:
Vср (m)
=
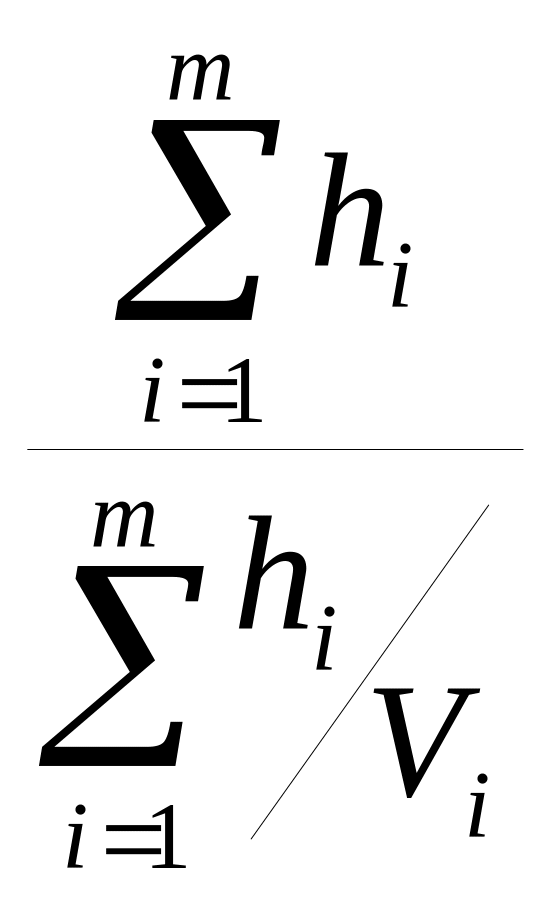 =
=
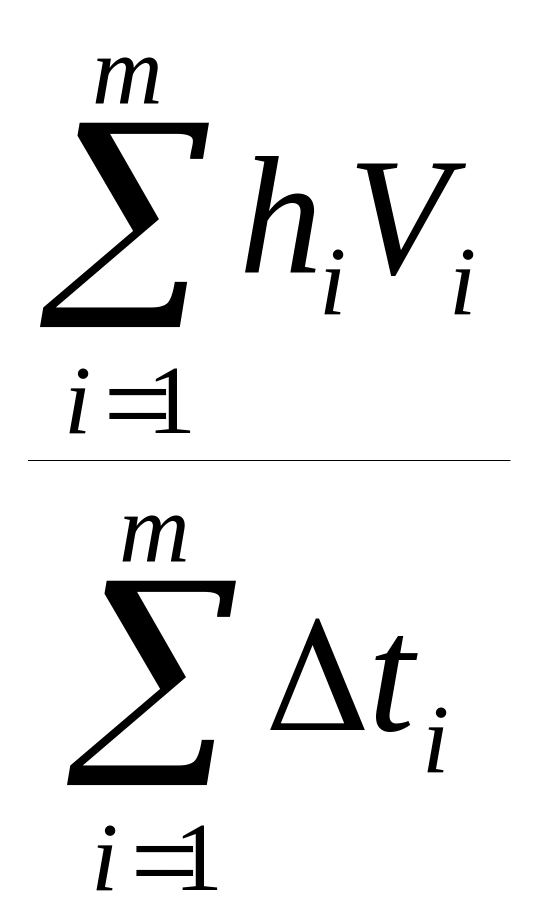
Для уяснения характера зависимости
эффективной скорости от соотношения
скоростей в разрезе и параметра луча p
исследуем уравнение (9) применительно
к среде с двумя отражающими границами.
Рассмотрим случаи, когда соотношение
пластовых скоростей в первом и втором
слое n =
![]() = {0.75, 0.5, 0.25} для pV1
= sin 1
= {0, 0.1, 0.15}
= {0.75, 0.5, 0.25} для pV1
= sin 1
= {0, 0.1, 0.15}

Из рассмотрения графиков можно сделать следующие выводы:
Минимальные отклонения Vэф от Vср наблюдаются при pV1 = 0, т.е при Vэф = Ve.
Максимальные отклонения Vэф от Vср наблюдаются при равной толщине слоев, т.е при h1 = h2.
Отклонения Vэф от Vср увеличиваются при увеличении скоростной дифференциации разреза
