§5. Доверительные интервалы.

Выше рассмотренная оценка параметра являлась точечной (одним числом). При выборке большого объема точечная оценка параметра близка к самому параметру. Однако, если число наблюдений мало, то возможно значительное расхождение между и t.

Чтобы получить представление о точности и надежности оценки параметра используют интервальную оценку параметра. Параметр t приближают некоторым интервалом ( ₁; ₂).

Интервальной оценкой параметра t называется числовой интервал ( ₁; ₂), который с заданной вероятностью γ накрывает неизвестное значение параметра t. Такой интервал ( ₁; ₂) называется доверительным интервалом, вероятность γ – доверительной вероятностью.

Заметим, что ₁ и ₂ находятся по выборочным данным, т.е. случайные величины, а t – некоторое определенное, хотя и неизвестное нам, число. Рассмотрим вопрос о построении доверительного интервала ( ₁; ₂) для непрерывной случайной величины Х ,имеющей нормальное распределение. Именно эта задача имеет большое практическое значение, особенно при обработке результатов измерений. Будем искать доверительный интервал для математического ожидания, когда σ известно, и когда σ неизвестно. Напомним, что плотность распределения вероятностей в случае

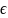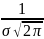
Х N(m; σ ): f(х) = 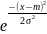, где m – математическое ожидание, σ – среднее квадратическое отклонение.

Доверительный интервал для m при известном σ.

Пусть непрерывная случайная величина Х имеет нормальное распределение Х N(m; σ ). Случайная величина (х) = также будет подчинена нормальному закону распределения (результаты опытов х₁, х₂, . . . , х_n – независимые случайные величины, распределенные нормально с параметрами m и σ).

При этом М( (х)) = м(х) = m,

D( (x)) = = 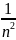n D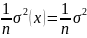(x) = => (x)) =

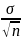
Тогда параметры распределения случайной величины (х) : (m; ) .

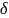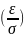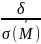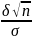Найдем такое , чтобы P( -δ < m < +δ) = γ. Воспользуемся формулой для нахождения вероятности попадания в интервал нормально распределенной случайной величины: P(׀x-m׀ < ε) = 2Ф , где Ф(х) – функция Лапласа. Тогда: P( -δ < m < +δ) = P(׀m- ׀< δ) = P(׀ – m׀ < δ) = 2Ф ( ) = 2Ф( ) = γ.

Обозначим t = , находится t по таблицам значений функции Лапласа из условия Ф(t) = 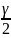. Тогда интервал ( - δ; + δ) или ( - ; + ) с заданной вероятностью γ накрывает неизвестное значение m. Таким образом, доверительным интервалом для m является интервал ( - ; + ), где t находится из условия Ф(t) = .

Пример. Произведено 5 независимых испытаний над непрерывной случайной величиной Х , распределенной нормально с σ =2:

i	1	2	3	4	5
xi	-25	34	-20	10	21

Найти оценку для М(х) и построить для нее 90% доверительный интервал. Решение: (х) = 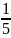(-25+34-20+10+21) = 4 γ = 0,9 => Ф(t) = 0,45 => t = 1,65 = ≈ 1,47 => 90% доверительным интервалом будет: (4 - 1,47; 4 + 1,47) или (2,53; 5,47).