
- •Статистическая проверка гипотез (статистические критерии)
- •Основные типы гипотез, проверяемых в ходе статистического анализа и моделирования
- •Гипотезы о типе закона распределения исследуемой случайной величины
- •Гипотезы об однородности двух или нескольких обрабатываемых выборок или нескольких характеристик анализируемых совокупностей
- •Гипотезы о числовых значениях параметров исследуемой генеральной совокупности
- •Гипотезы об общем виде модели, описывающей статистическую зависимость между признаками
- •Общая логическая схема статистического критерия
- •Построение статистического критерия; принцип отношения правдоподобия
- •Сущность принципа отношения правдоподобия
- •Методы проверки статистических гипотез: примеры статистических критериев Критерии согласия
- •Критерий согласия Пирсона
- •Критерий однородности Смирнова
- •Критерий Стьюдента ( -критерий)
- •-Критерий однородности дисперсий
- •Проверка гипотез о числовых значениях параметров
- •Критерии проверки гипотез о числовом значении параметра биноминального распределения
- •Критерии проверки гипотез о среднем значении нормальной генеральной совокупности
- •Критерий проверки гипотезы о значении дисперсии нормальной генеральной совокупности
- •Последовательный критерий отношения правдоподобия (критерий Вальда) и его свойства
Построение статистического критерия; принцип отношения правдоподобия
Выясним, как конкретно получаются те функции от результатов наблюдения (критические статистики ), по значениям которых принимается окончательное решение о том, соответствует ли проверяемая гипотеза имеющимся у нас данным или противоречит им.
Сущность принципа отношения правдоподобия
в общем случае
представление о сравнительной
правдоподобности имеющихся наблюдений
![]() (в отношении проверяемой и альтернативной
гипотез) дает нам сопоставление
соответствующих функций правдоподобия
и, в частности, их отношение
(в отношении проверяемой и альтернативной
гипотез) дает нам сопоставление
соответствующих функций правдоподобия
и, в частности, их отношение
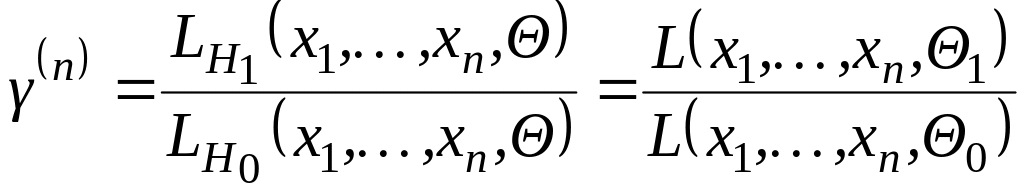 , (1)
, (1)
где
![]() и
– значения функций правдоподобия
наблюдений
и
– значения функций правдоподобия
наблюдений
![]() ,
вычисленные в предположении справедливости
соответственно гипотез
,
вычисленные в предположении справедливости
соответственно гипотез
![]() и
и
![]() .
Очевидно, чем правдоподобнее наблюдения
в условиях гипотезы
,
тем больше функция правдоподобия
.
Очевидно, чем правдоподобнее наблюдения
в условиях гипотезы
,
тем больше функция правдоподобия
![]() и тем меньше величина
.
Если
– плотность распределения статистики
при условии справедливости гипотезы
,
то построение критерия проверки гипотезы
с заданным уровнем значимости
и тем меньше величина
.
Если
– плотность распределения статистики
при условии справедливости гипотезы
,
то построение критерия проверки гипотезы
с заданным уровнем значимости
![]() сводится к определению
-ой
точки
сводится к определению
-ой
точки
![]() распределения
и к реализации следующего правила:
распределения
и к реализации следующего правила:
если
![]() ,
то гипотеза
отвергается с вероятностью ошибиться,
равной
,
так как в соответствии с законом
,
то гипотеза
отвергается с вероятностью ошибиться,
равной
,
так как в соответствии с законом
![]() и при справедливости гипотезы
возможно осуществление события
и при справедливости гипотезы
возможно осуществление события
![]() с вероятностью
,
т.е.
с вероятностью
,
т.е.
![]() ;
;
если
![]() ,
то гипотеза
,
то гипотеза
![]() не отвергается.
не отвергается.
Критерии, основанные на статистиках вида (1) и процедуре, рассмотренной выше, называются критерии отношения правдоподобия. Их практическая реализуемость и предпочтительность по отношению к другим возможным критериям основаны на следующих фактах.
Критерии отношения правдоподобия являются наиболее мощными среди всех других возможных критериев.
Плотность распределения критической статистики , как правило, без труда восстанавливается по функции правдоподобия
 наблюдаемой случайной величины.
наблюдаемой случайной величины.
Методы проверки статистических гипотез: примеры статистических критериев Критерии согласия
Критерии согласия предназначены для статистической проверки гипотез о модельном виде закона распределения вероятностей исследуемой случайной величины.
Критерий согласия Пирсона
Этот критерий
позволяет проверять гипотезы вида
![]() как для дискретных, так и для непрерывных
случайных величин, когда параметры
как для дискретных, так и для непрерывных
случайных величин, когда параметры
![]() известны или являются неизвестными.
Если гипотеза
известны или являются неизвестными.
Если гипотеза
![]() истинна, то при некоторых, достаточно
общих условиях распределение критической
статистики
истинна, то при некоторых, достаточно
общих условиях распределение критической
статистики
 (2)
(2)
сходится (при
![]() )
к
)
к
![]() -распределению.
-распределению.
В непрерывном
случае статистика (2) строится по
группированным данным.
![]() – это общее число интервалов;
– это общее число интервалов;
![]() – число выборочных данных, попавших в
– число выборочных данных, попавших в
![]() -ый
интервал;
-ый
интервал;
![]() – векторный параметр, который участвует
в выражении модельной функции распределения
– векторный параметр, который участвует
в выражении модельной функции распределения
![]() ,
а
,
а
![]() – его состоятельная оценка (более
корректным способом оценивания считается
тот, при котором в качестве
используется оценка максимального
правдоподобия, построенная по
группированным данным);
– его состоятельная оценка (более
корректным способом оценивания считается
тот, при котором в качестве
используется оценка максимального
правдоподобия, построенная по
группированным данным);
![]() – число неизвестных параметров,
оцениваемых по выборке (в случае известных
значений параметров
– число неизвестных параметров,
оцениваемых по выборке (в случае известных
значений параметров
![]() );
);
![]() – это результат модельного расчета
вероятности попасть в
-ый
интервал, т.е.
– это результат модельного расчета
вероятности попасть в
-ый
интервал, т.е.
![]() , (3)
, (3)
где
![]() – соответственно левый и правый концы
в
-го
интервала.
– соответственно левый и правый концы
в
-го
интервала.
Случай анализа
дискретной случайной величины отличается
от предыдущего тем, что мы работаем с
исходной (а не группированной) выборкой;
– число выборочных данных, равных
-му
возможному значению
![]() ,
,
![]() – число всех возможных значений случайной
величины;
– число всех возможных значений случайной
величины;
![]() . (4)
. (4)
Процедура проверки гипотезы критерием Пирсона.
По данным выборки
 найти состоятельную оценку
найти состоятельную оценку
 параметров
параметров
 .
.вычислить значение критической статистики .
по заданному уровню значимости критерия из таблиц процентных точек -распределения находим и -ые точки
 и
и
 «хи-квадрат» распределения с
«хи-квадрат» распределения с
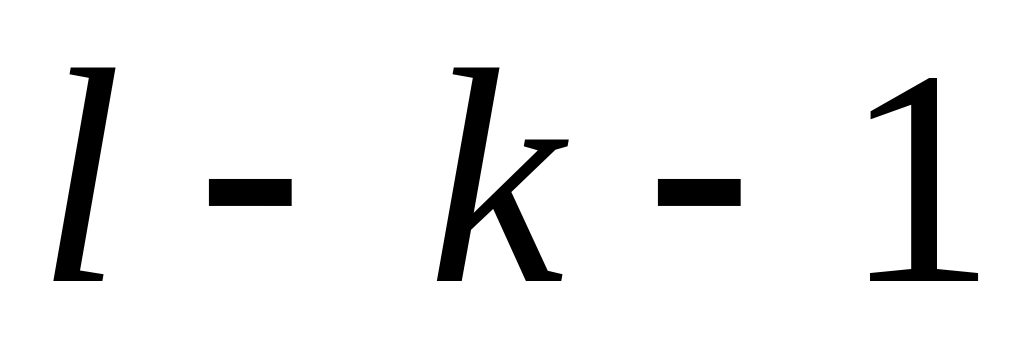 степенями свободы.
степенями свободы.если
 ,
то гипотеза не отклоняется; если же
,
то гипотеза не отклоняется; если же
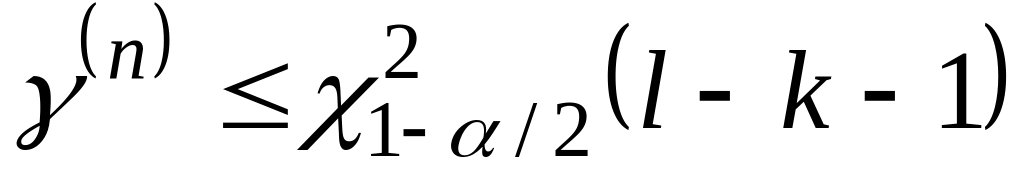 или
или
 ,
то гипотеза отклоняется. Отвержение
выдвинутой гипотезы в случае «слишком
маленьких» значений статистики критерия
на первый взгляд противоречит здравому
смыслу. Действительно, статистика
характеризует степень отклонения
эмпирического распределения случайной
величины
от гипотетического
,
то гипотеза отклоняется. Отвержение
выдвинутой гипотезы в случае «слишком
маленьких» значений статистики критерия
на первый взгляд противоречит здравому
смыслу. Действительно, статистика
характеризует степень отклонения
эмпирического распределения случайной
величины
от гипотетического
 ;
чем меньше
,
тем меньше это отклонение. Но хотя
и является мерой отклонения гипотетического
закона
;
чем меньше
,
тем меньше это отклонение. Но хотя
и является мерой отклонения гипотетического
закона
 от истинного, но мерой случайной, т.е.
величиной, подверженной обязательному
неконтролируемому рассеянию. В этом
отношении одинаково неправдоподобными
следует считать как слишком большие
значения
,
так и слишком малые. Слишком малые
значения
могут говорить о неудачном выборе
закона
(искусственное завышение числа
параметров, от которых этот закон
зависит). Другими причинами могут
являться нарушения корректности или
объективности техники выборочного
обследования.
от истинного, но мерой случайной, т.е.
величиной, подверженной обязательному
неконтролируемому рассеянию. В этом
отношении одинаково неправдоподобными
следует считать как слишком большие
значения
,
так и слишком малые. Слишком малые
значения
могут говорить о неудачном выборе
закона
(искусственное завышение числа
параметров, от которых этот закон
зависит). Другими причинами могут
являться нарушения корректности или
объективности техники выборочного
обследования.
