Равновесие плоских шарнирных механизмов
Плоский шарнирный
механизм (рис. 7), расположенный в
вертикальной плоскости, находится в
равновесии под действием внешнего
момента
![]() ,
приложенного к произвольному звену.
,
приложенного к произвольному звену.
Определить реакции внешних и внутренних связей, а также величину уравновешивающего момента в произвольном положении механизма. Рассмотреть следующие варианты приложения внешних сил:
![]() .
.

Рис. 7
Исходные данные:

Решение
Для решения
поставленной задачи выберем правую
систему координат, начало которой
расположим в подшипнике
![]() .
Рассмотрим механизм в произвольном
положении и изобразим силы, действующие
на него (рис. 8):
.
Рассмотрим механизм в произвольном
положении и изобразим силы, действующие
на него (рис. 8):
![]() – силы тяжести
звеньев;
– силы тяжести
звеньев;
![]() – уравновешивающий
момент, приложенный к ведущему звену
– уравновешивающий
момент, приложенный к ведущему звену
![]() ;
;
![]() – реакции шарнирных
опор.
– реакции шарнирных
опор.

Рис. 8
На механизм
действует произвольная плоская система
сил, для которой можно записать не
более трех условий равновесия.
Неизвестных сил, действующих на механизм
семь:
![]() .
.
Расчленим плоский шарнирный механизм по шарнирам на отдельные звенья и изобразим реакции внешних и внутренних связей каждого звена и рассмотрим равновесие всех звеньев (рис. 9).

Рис. 9
На кривошип
действуют внешние силы
![]() ,
пара сил с моментом
,
пара сил с моментом
![]() ,
а также реакция шарнира
-
,
а также реакция шарнира
-
![]() .
.
На шатун
кроме силы тяжести
![]() действуют реакции,
действуют реакции,
![]() .
.
На кривошип
![]() действуют силы
действуют силы
![]() и внутренние реакции
и внутренние реакции
![]() .
.
На шатун
![]() кроме силы тяжести
кроме силы тяжести
![]() действуют реакции
действуют реакции
![]() .
.
На кривошип
![]() действуют силы
действуют силы
![]() и внутренние реакции
и внутренние реакции
![]() .
.
Таким образом,
на звенья механизма действует
пятнадцать неизвестных сил: пара сил
,
а также реакции внешних и внутренних
связей
![]()
![]()
![]() и
и
![]()
Звенья
![]() механизма находятся в равновесии под
действием произвольных плоских систем
сил. Для каждого звена запишем следующие
условия равновесия:
механизма находятся в равновесии под
действием произвольных плоских систем
сил. Для каждого звена запишем следующие
условия равновесия:

Каждое из условий,
обеспечивающее равенства нулю главного
вектора системы сил
![]() ,
на плоскости эквивалентно двум
уравнениям равновесия, а условия
равновесия моментов
,
на плоскости эквивалентно двум
уравнениям равновесия, а условия
равновесия моментов
![]() ,
на плоскости эквивалентно одному
уравнению равновесия. Таким образом,
условиям равновесия в векторной форме
соответствуют 15 линейным алгебраических
уравнений равновесия с 15-ю неизвестными,
и задача является статически определимой.
,
на плоскости эквивалентно одному
уравнению равновесия. Таким образом,
условиям равновесия в векторной форме
соответствуют 15 линейным алгебраических
уравнений равновесия с 15-ю неизвестными,
и задача является статически определимой.
Составляя уравнения равновесия, в векторной форме получим:


Здесь,
![]() - радиус-векторы, определяющие положение
соответствующих точек механизма на
плоскости.
- радиус-векторы, определяющие положение
соответствующих точек механизма на
плоскости.
Ориентация векторов
на плоскости задается с помощью углов
и
![]() ,
которые можно определить с помощью
уравнений геометрических связей,
записанных для узловых точек плоского
механизма.
,
которые можно определить с помощью
уравнений геометрических связей,
записанных для узловых точек плоского
механизма.
Составим с помощью пакета MathCAD уравнения равновесия в символьном виде.
Задание векторов, определяющих положение точек приложения сил:
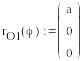
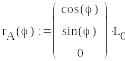
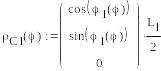
![]()
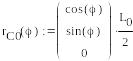
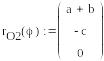

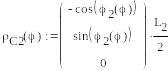
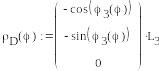
![]()
![]()
![]()

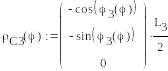
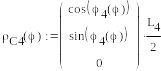
![]()
![]()
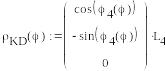
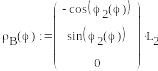
Формирование векторов активных сил:
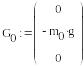
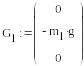
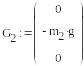
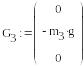
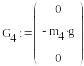
Формирование векторов неизвестных сил и реакций связей:
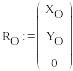
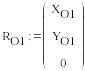
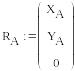

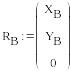

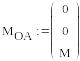

![]()
![]()
![]()
![]()
Вычисление главных векторов и главных моментов внешних сил, действующих на звенья плоского механизма.
Кривошип :
![]()
![]()
Шатун :
![]()
![]()
Кривошип :
![]()
![]()
Шатун :
![]()
![]()
Кривошип :
![]()
![]()
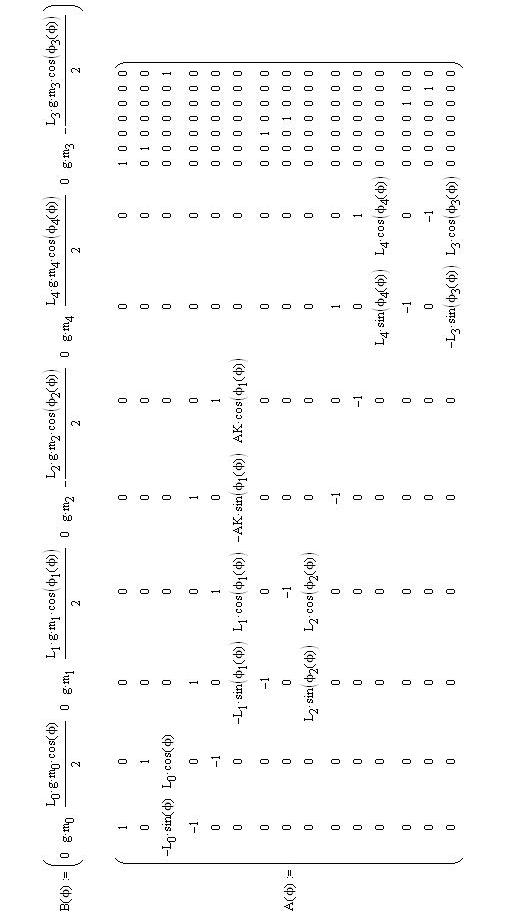
Формирование уравнений равновесия:
![]()

Решение полученной системы уравнений может быть найдено в MathCAD с помощью блока решений Given-Find. Однако, наиболее эффективным способом решения и анализа результатов вычислений систем линейных алгебраических уравнений является матричный метод. Для его применения представим уравнения равновесия в матричной форме:
![]()
где
– матрица коэффициентов при неизвестных
величинах,
![]() – вектор неизвестных,
– вектор правой части (известных
слагаемых в уравнениях равновесия)
системы алгебраических уравнений.
– вектор неизвестных,
– вектор правой части (известных
слагаемых в уравнениях равновесия)
системы алгебраических уравнений.
Этому уравнению
соответствует решение вида
![]() .
.
При этом определитель матрицы не должен быть равен нулю
![]() .
.
Уравнения равновесия для других вариантов приложения уравновешивающих сил составляются аналогично.
Теперь выполним численный расчет.
Введем исходные данные:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Вычисление вспомогательных функций и решение уравнений геометрической связи:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Решение системы уравнений:
![]()
Формирование реакций внешних и внутренних связей:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Построение графиков функций.
![]()
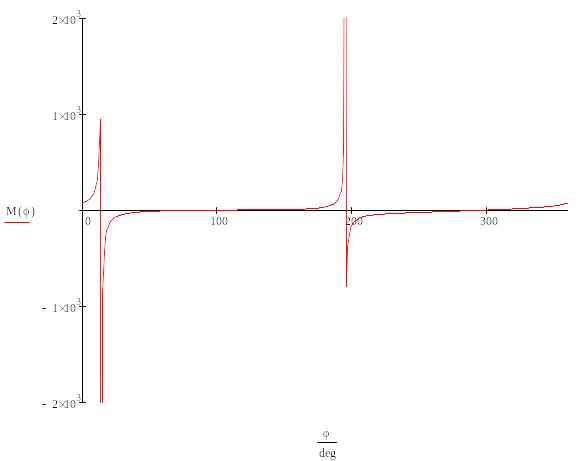
Зависимость момента пары сил, обеспечивающего равновесие механизма, от угла поворота ведущего звена:
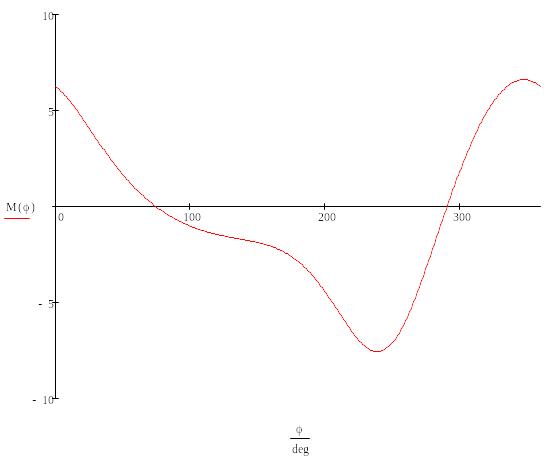
Зависимость реакций внешних и внутренних связей от угла поворота ведущего звена:
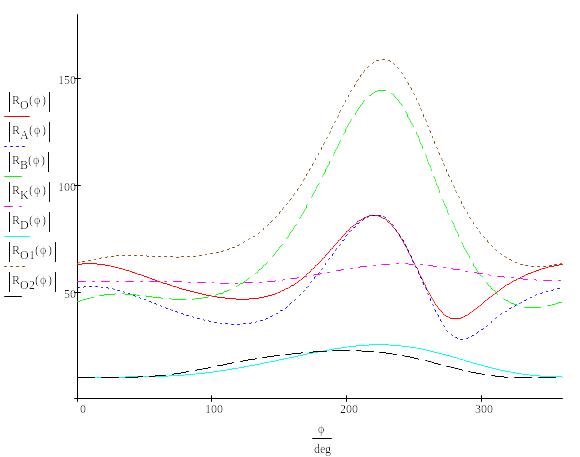
Расчет плоского
механизма при действии момента
![]() ,
приложенного к звену
,
приложенного к звену
Зависимость момента пары сил, обеспечивающего равновесие механизма, от угла поворота ведущего звена:
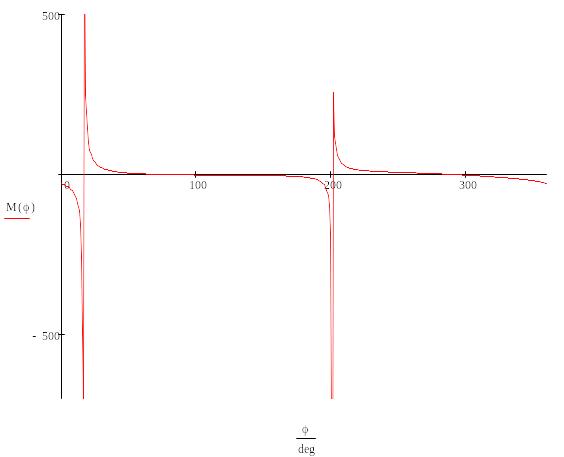
Расчет плоского
механизма при действии момента
![]() ,
приложенного к звену
,
приложенного к звену
Зависимость момента пары сил, обеспечивающего равновесие механизма, от угла поворота ведущего звена: