3. Вторая производная и производные высших порядков.

Если функция дифференцируема, то ее производная называется производной второго порядка и обозначается или , т.е. .

Производные порядка выше первого называется производными высших порядков.

Примеры. Найти производные высших порядков:

1) ;

Решение. . .

2) ;

Решение. . . .

3) ; 4) ;

Интегральное исчисление Неопределенный интеграл.

1. Неопределенный интеграл и его свойства.

Определение. Совокупность всех первообразных функций на множестве М называется неопределенным интегралом (на этом множестве) и обозначается символом .

В этом обозначении знак называется знаком интеграла, выражение - подынтегральным выражением, а функция - подынтегральной функцией.

Если F (x) – одна из первообразных функций для функции на множестве М, то

, где С – любая постоянная. (1)

Пример. .

Замечание 1. Если F (x) - первообразная функции на множестве М, то в формуле (1) под знаком интеграла стоит дифференциал функции F (x): d F (x) = F' (x)d х = dх.

Будем считать по определению, что = F' (x)d х = d F (x)

Замечание 2. Наличие постоянной С делает задачу нахождения функции по ее производной не вполне определенной, отсюда происходит и само название «неопределенный интеграл».

Свойства неопределенного интеграла

1. Производная неопределенного интеграла равна подынтегральной функции, т. е.

2. Постоянный множитель подынтегрального выражения можно выносить за знак интеграла, т.е. т ; т – постоянная величина ≠ 0.

3. Интеграл от алгебраической суммы функций равен алгебраической сумме интегралов от этих функций, т.е. .

Пример. Найти интеграл .

= .

Замечание 3. При интегрировании алгебраической суммы функций принято записывать только одну произвольную постоянную, т.к. алгебраическая сумма произвольных постоянных есть постоянная.

4. Дифференциал неопределенного интеграла равен подынтегральному выражению, т.е.

.

Это означает, что знак дифференциала аннулирует знак интеграла.

Таблица формул интегрирования

1.

2.

3.

5.

6.

7.

8.

9.

10.

11.

12. , или

13. , или

2. Метод интегрирования по частям.

Интегрированием по частям называется сведение данного интеграла к интегралу c помощью формулы

(1)

Этот прием ведет к цели, если находится легче, чем .

Примеры. Найти неопределенные интегралы интегрированием по частям:

1) ; 2) ; 3)

Методические указания к выполнению упражнения:

1. 

2) 3)

Вывод: 1) В интегралах вида ; ;

где Р(х) – многочлен относительно х, а – некоторое число, полагают u = Р(х)

2. В интегралах вида ; ; ; ; ;

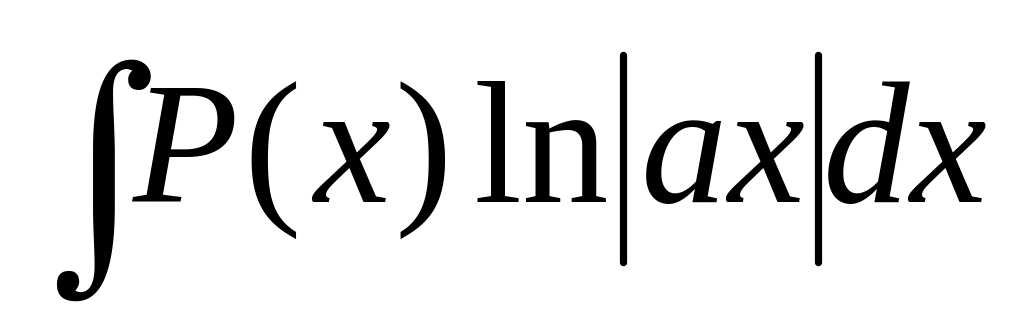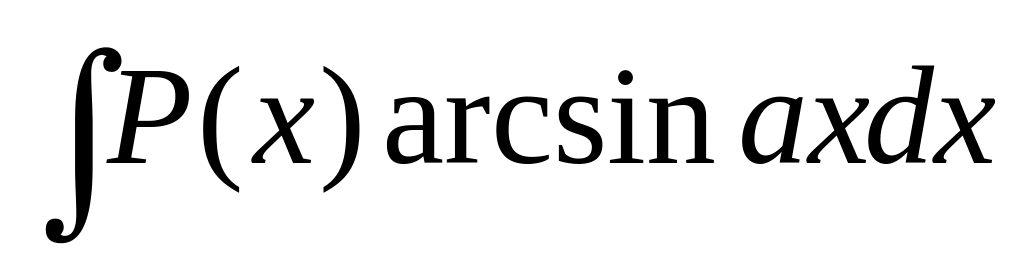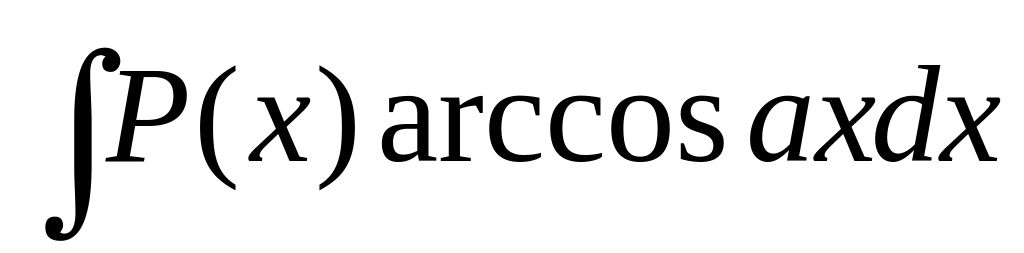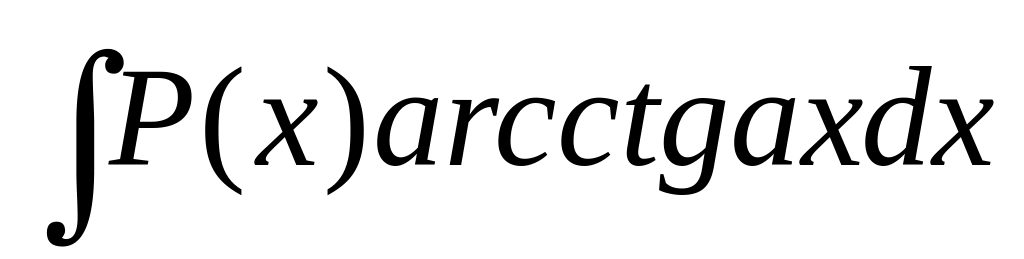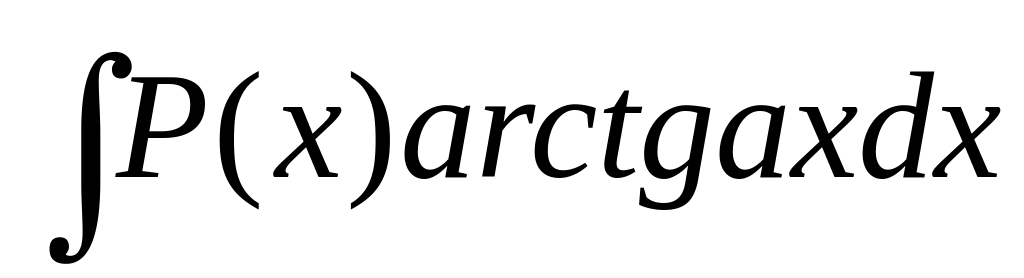полагают Р(х)dx = dv

3. В интегралах вида ;

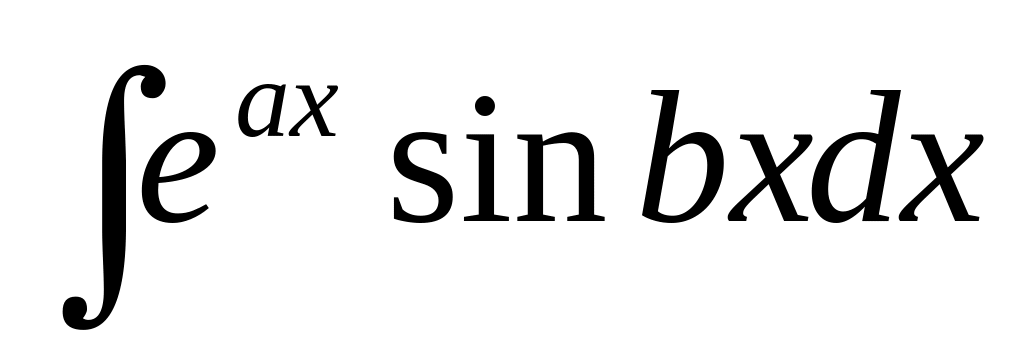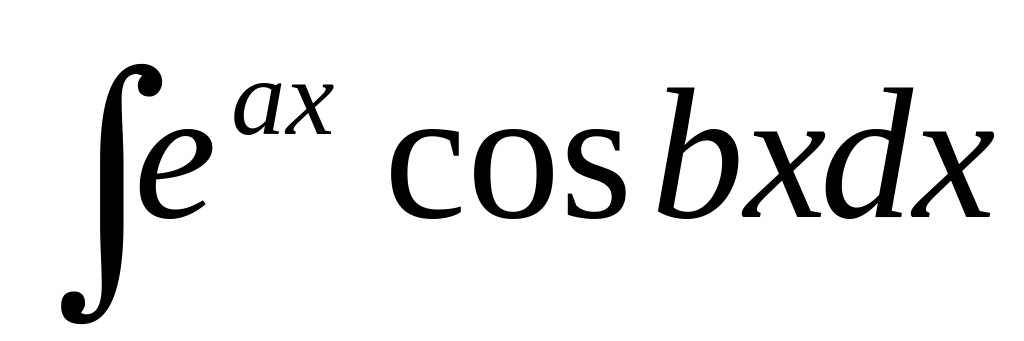
где а и b - числа, за u можно принять любую из функции , или sin bx, или cos bx.

Определенный интеграл

1. Определенный интеграл и его свойства.

Напомним, что приращением аргумента х при его изменении от х = а до х = b называется разность b – а, а приращением функции F (x) при изменении аргумента от а до b называется разность F (b) - F (а).

Определение. Приращение F (b) - F (а) любой из первообразных функций F (x) + С при изменении аргумента от х = а до х = b называется определенным интегралом и обозначается

, непрерывна на промежутке (а; b) .

а – нижний предел, b – верхний предел.

Теорема. Если функция непрерывна на промежутке (а; b) и F (x) – какая-либо ее первообразная на (а; b), то имеет место формула

= F (b) - F (а).

Это равенство называется формулой Ньютона-Лейбница.

Формула Ньютона-Лейбница дает удобный способ вычисления определенного интеграла.

Для вычисления определенного интеграла нужно найти соответствующий неопределенный интеграл, в полученное выражение подставить вместо х сначала верхний предел, а затем нижний предел определенного интеграла и из первого результата вычесть второй: F (b) - F (а).