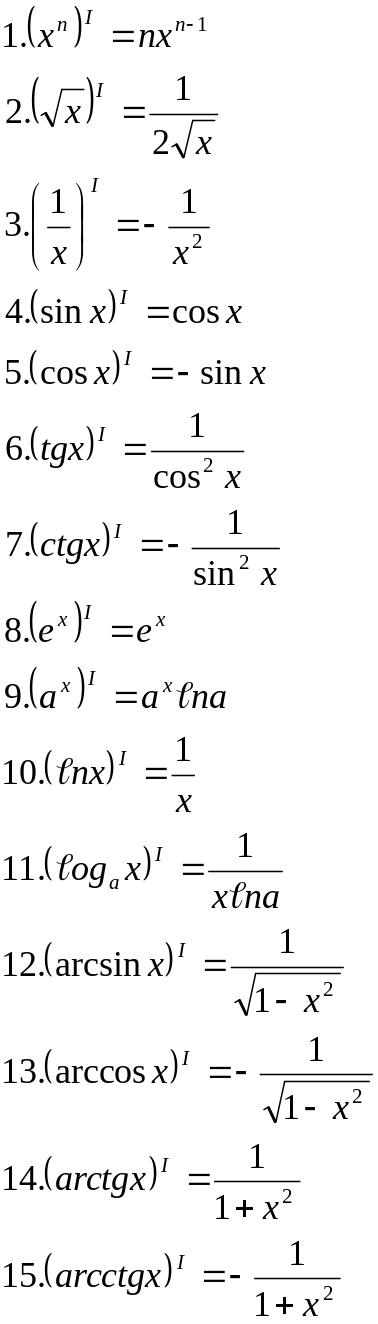2. Вычисление пределов.
1.
.
Указание.
Умножить числитель и знаменатель на
и сократить дробь на
.
2.
.
3. Методом подстановки.
а)
.
Решение.
Положим
,
тогда
и
при
.
Отсюда
=
=
=
.
б)
.
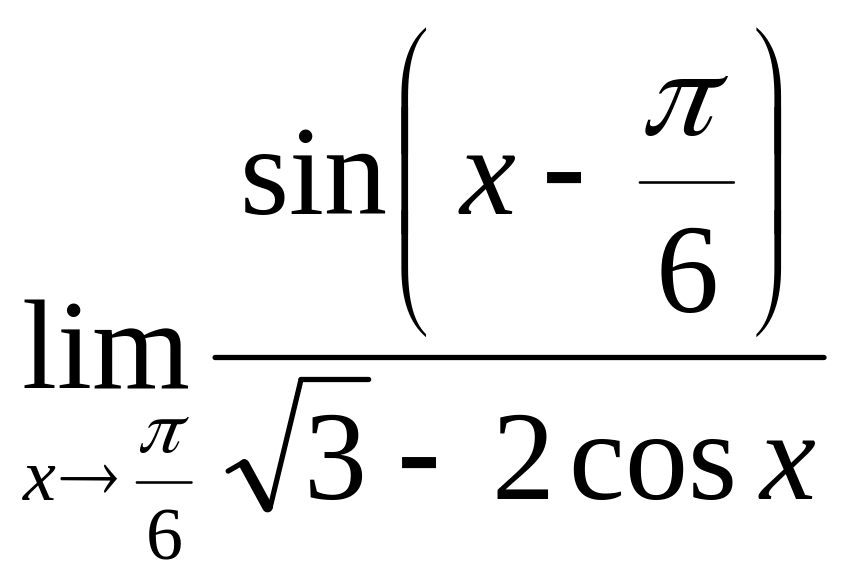Решение.
Положим
,
тогда
и
при
.
Отсюда
=
=
=
.
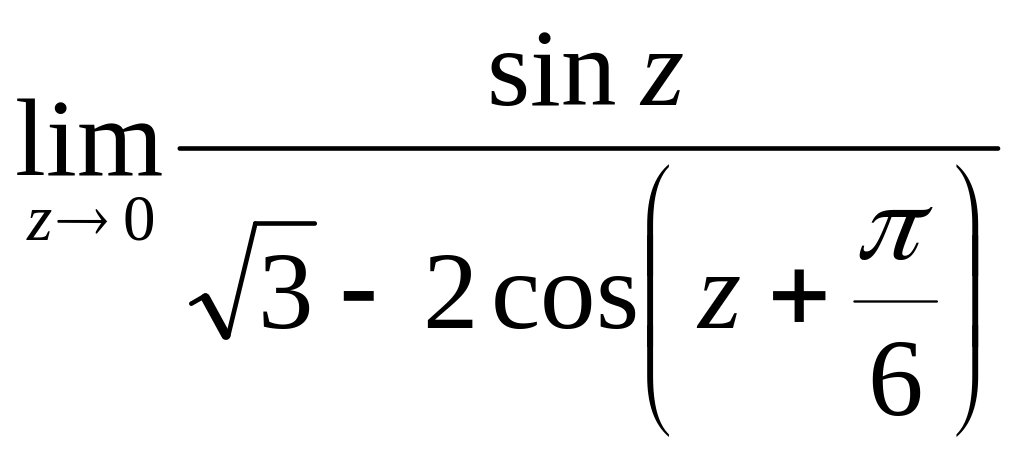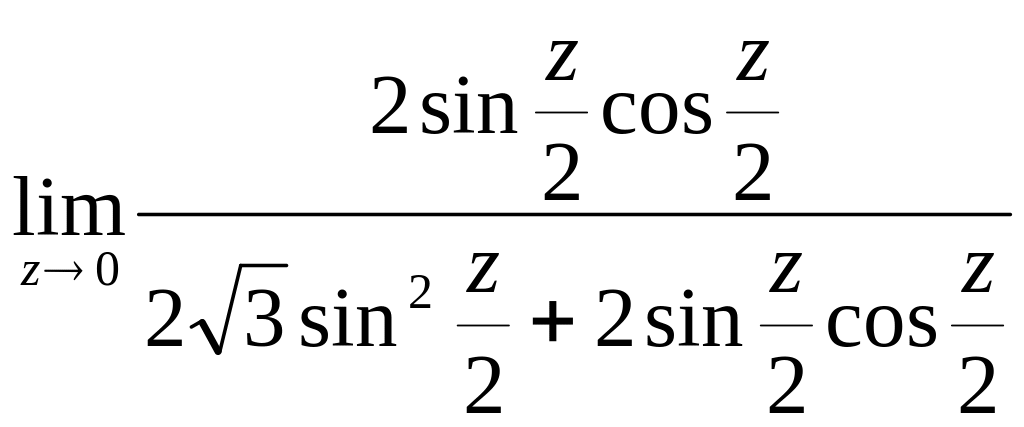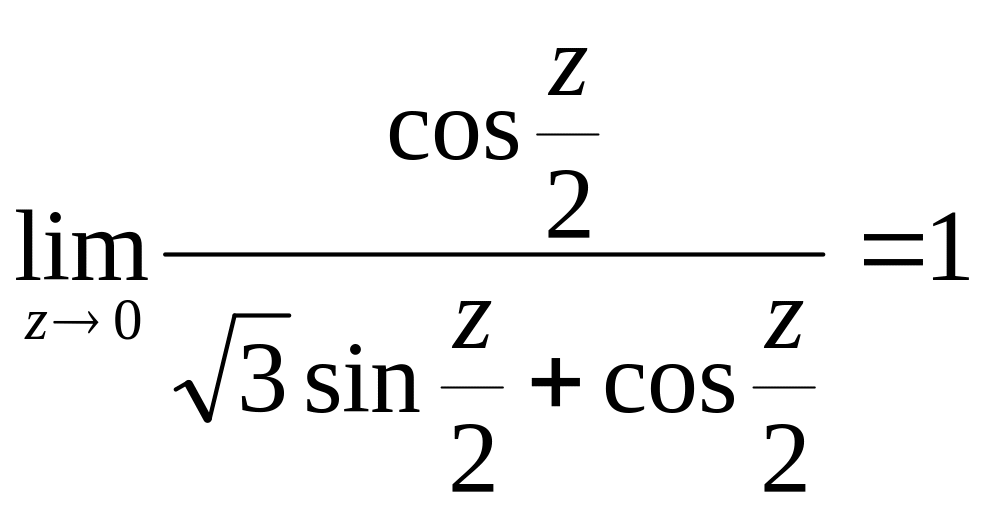3. Предел функции на бесконечности.
Рассмотрим
примеры на вычисление пределов функций
при
.
Пример1.
Найти
.
Решение.
Очевидно,
.
Поэтому по теореме (4)функция
- бесконечно малая, а значит и функция
тоже бесконечно малая при
,
т.е.
=
0.
Пример
2.
Найти
.
Решение.
Здесь
,
.
Говорят, что в этом случае имеем
неопределенность
вида
.
Для ее раскрытия числитель и знаменатель
дроби
почленно разделим на х
с наибольшим показателем степени, т. е.
на
.
Следовательно, получим:
.
Но
,
и
.
В результате имеем, что
.
Аналогично устанавливается, что при , дробно-рациональная функция стремиться либо к нулю, либо к бесконечности, либо к конечному числу, отличному от нуля, в зависимости от того, будет ли степень числителя меньше степени знаменателя, больше ее или равна ей.
Дифференциальное исчисление Производные функции.
1. Определение производной функции. Правила дифференцирования..
Производной функции в точке х0 называют предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремиться к нулю.
Итак, по определению
Производная
функции
есть некоторая функция
произведенная из данной функции.
Функция
,
имеющая производную в каждой точке
интервала
,
называется дифференцируемой
в этом интервале; операция нахождения
производной функции называется
дифференцированием.
Правила дифференцирования
Введем обозначения: С – постоянная;
х – аргумент;
u, v – функции от х
1.
Производная постоянной равна нулю:
2.
Производная независимой переменной
равна единице:
3.
Производная суммы функций равна сумме
производных этих функций.
4. Производная произведения двух функций равна производной первого сомножителя, умноженный на второй, плюс производная второго сомножителя, умноженный на первый.
5.
Постоянный множитель можно вынести за
знак производной:
6. Производная дроби равна дроби, знаменатель которой равен квадрату знаменателя данной дроби, а числитель равен производной числителя умноженный на знаменатель, минус производная знаменателя, на числитель.
7.
Производная сложной функции.
Формулы дифференцирования
Элементарные функции
|
Сложные функции
|
Пример
1. Найти
производную функции
и вычислить ее значение при
.
Решение.
.
Вычислим значение производной при :
.
Пример
2. Найти
производную функции
.
Решение.
.
Пример
3. Найти
производную функции
.
Решение.
=
.
2. Нахождение производных обратных тригонометрических функций.
Теорема:
Если
дифференцируемая функция
является обратной по отношению к функции
,
то ее производная вычисляется по формуле:
.
1.
Обратной
для этой функции, является функция
,
т.е.
.
.
Из тождества
.
Отсюда
.
2.
.
3.
.
4.
.
Примеры. Продифференцировать функцию:
1)
Решение.
.
2)
Решение.
.
3)
Решение.
.4)
.
5)
.