9. Двумерные случайные величины

Вектор , координаты которого есть случайные величины, заданные на одном и том же вероятностном пространстве, называется случайным вектором, а функция называется функцией распределения вероятности случайного вектора или двумерной случайной величины .

Если координаты вектора – дискретные случайные величины, то называют дискретным случайным вектором.

Закон распределения дискретной двумерной случайной величины представляет собой таблицу

			…
			…
			…
…	…	…	…	…

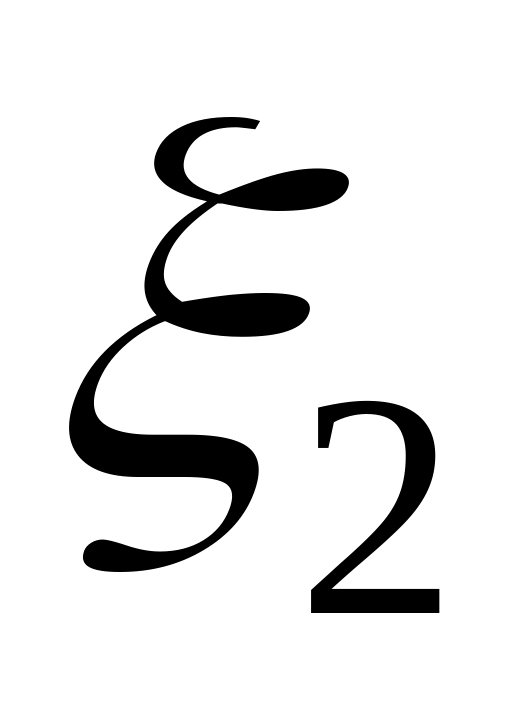
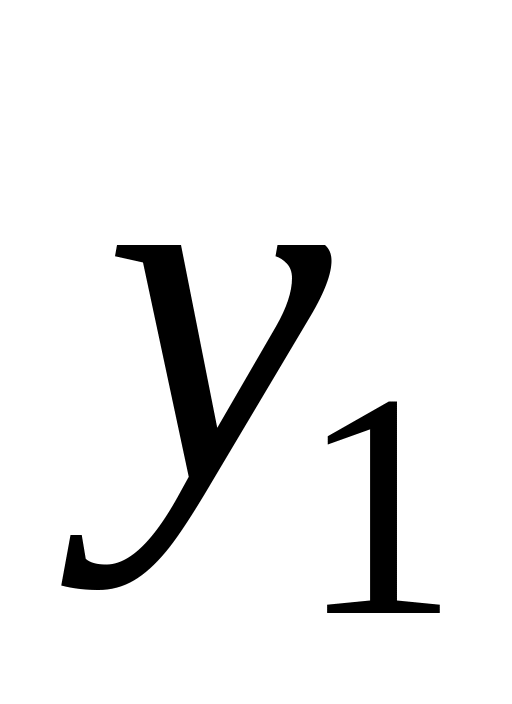
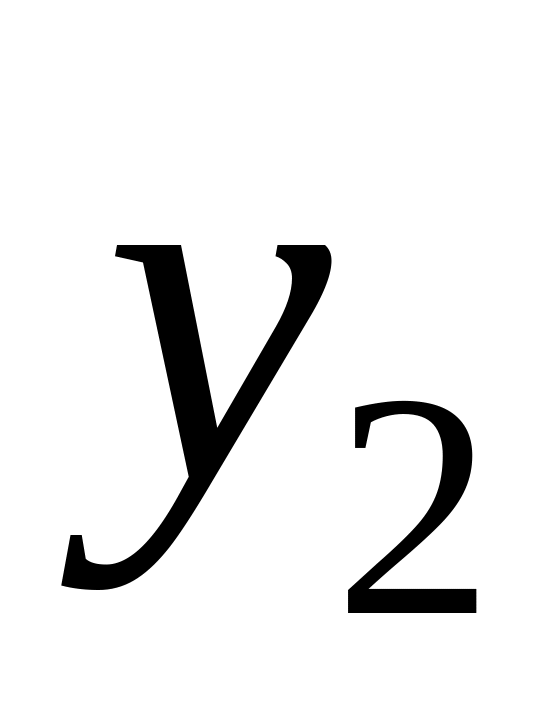
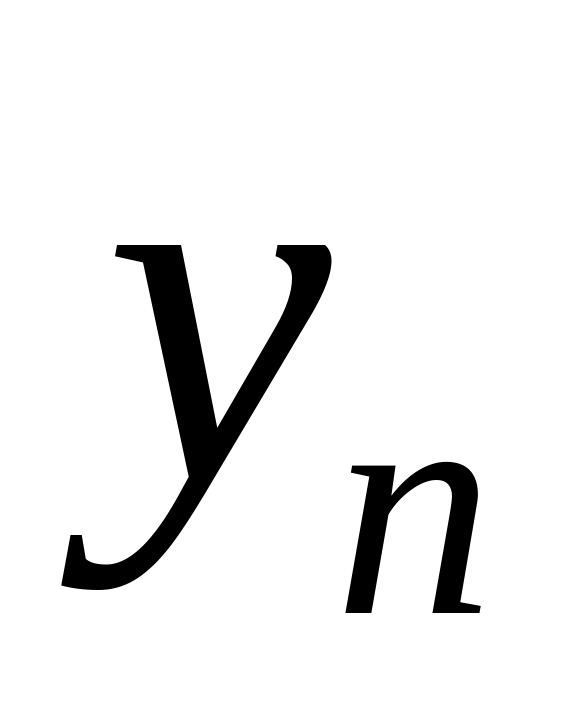
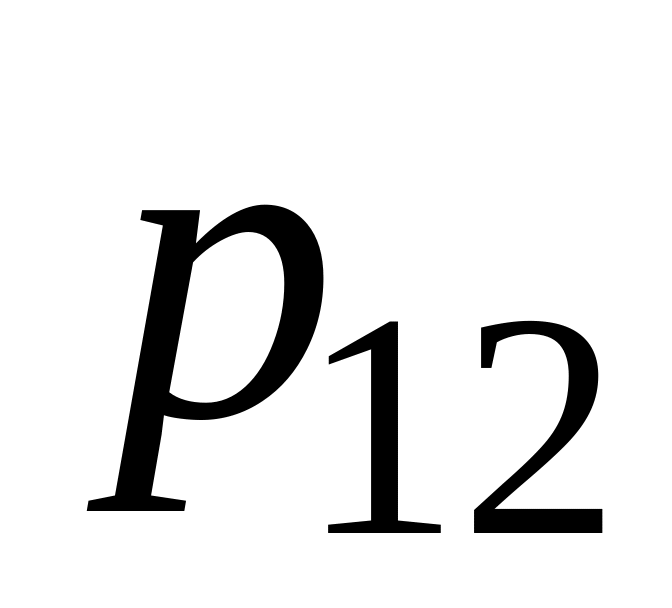
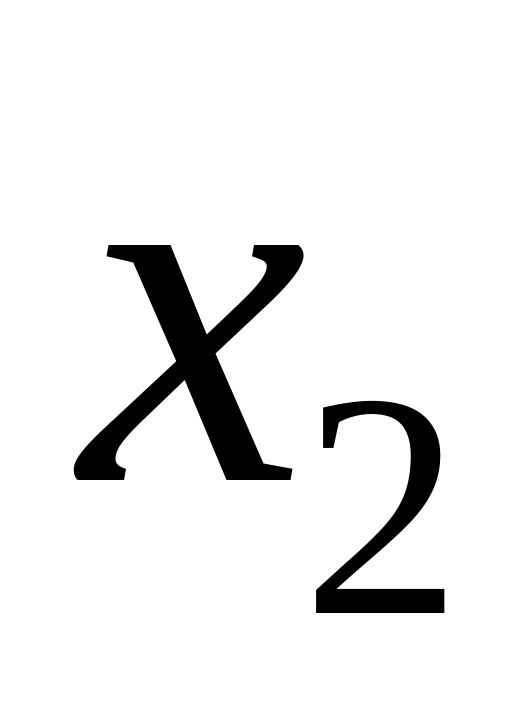
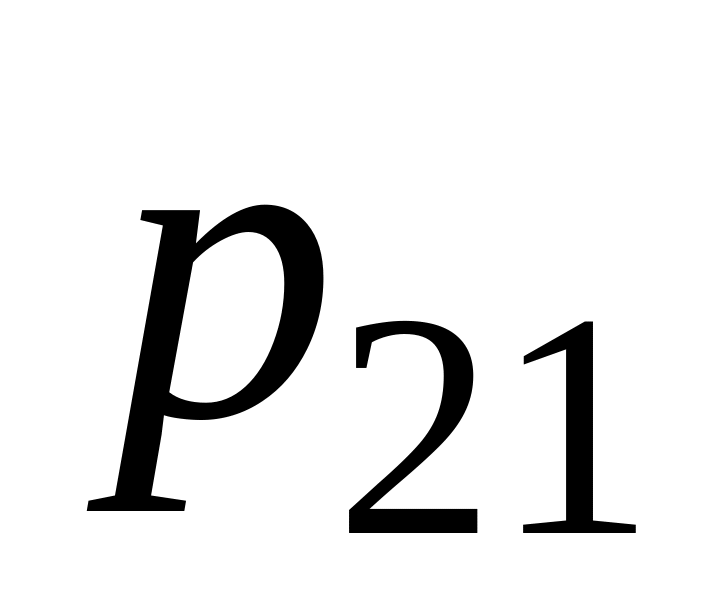
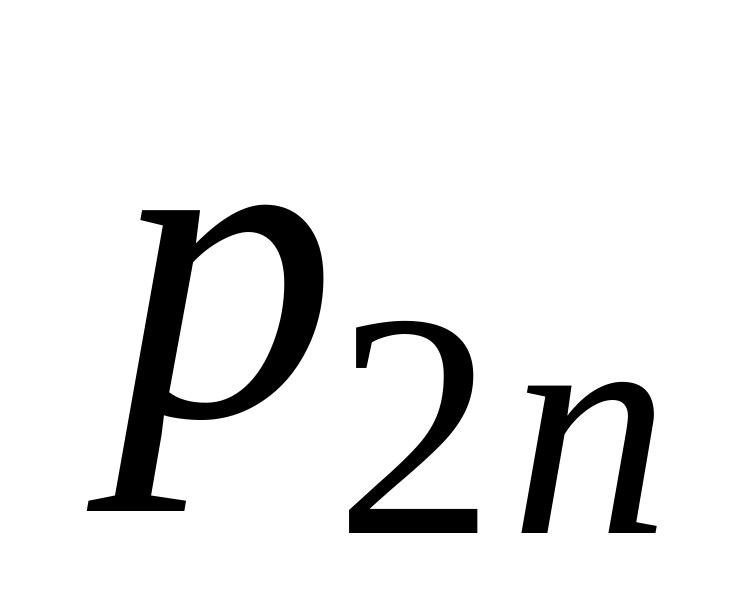
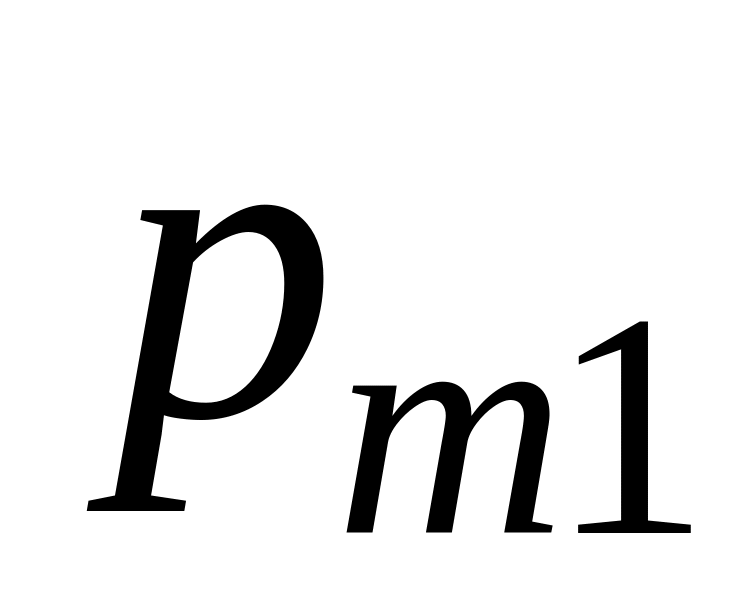
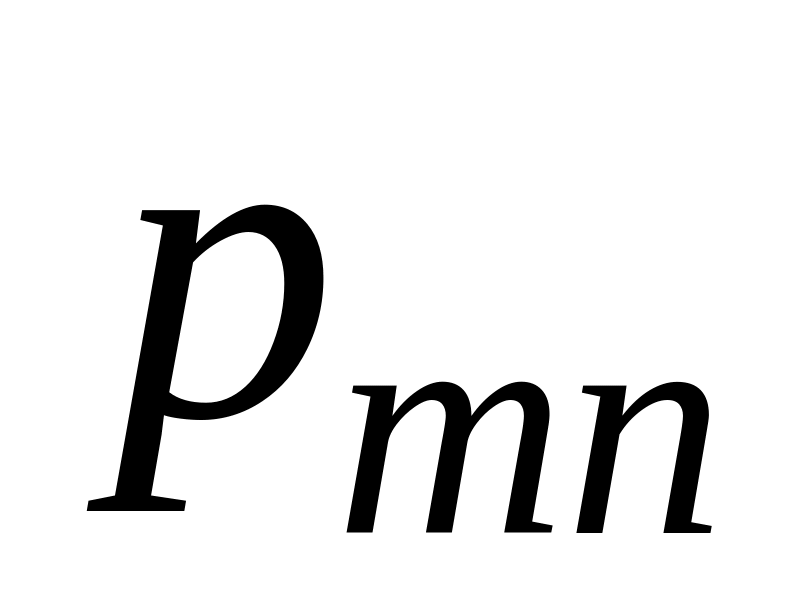
где Так же как и для одномерной дискретной случайной величины должно выполняться условие нормировки .

Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения составляющих, то есть случайных величин и . Для этого достаточно просуммировать вероятности по строкам и по столбцам соответственно. Знание законов распределения составляющих позволяет найти числовые характеристики составляющих, а также их корреляционный момент.

Если функцию распределения вероятности вектора можно представить в виде , то случайную величину называют непрерывной двумерной случайной величиной, а – ее плотностью распределения вероятности.

Свойства функции и плотности распределения вероятности

1) .

2) .

3) 0.

4) .

5) , , где и – функции распределения вероятности случайных величин и .

6) В любой точке непрерывности функции , .

7) .

8) .

9) .

10) , ,

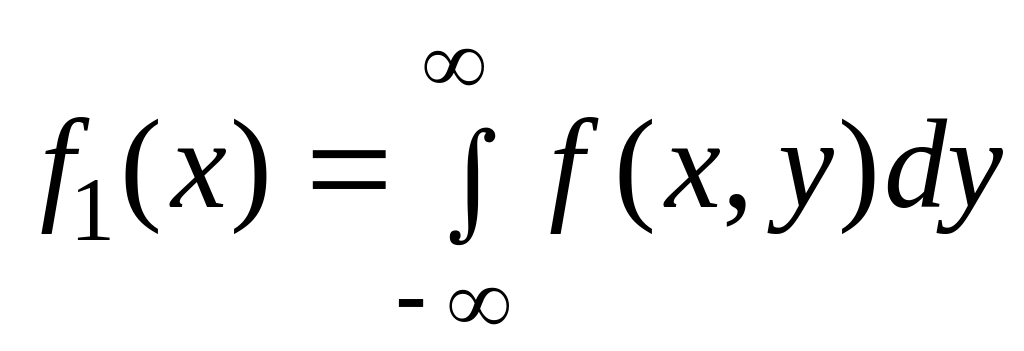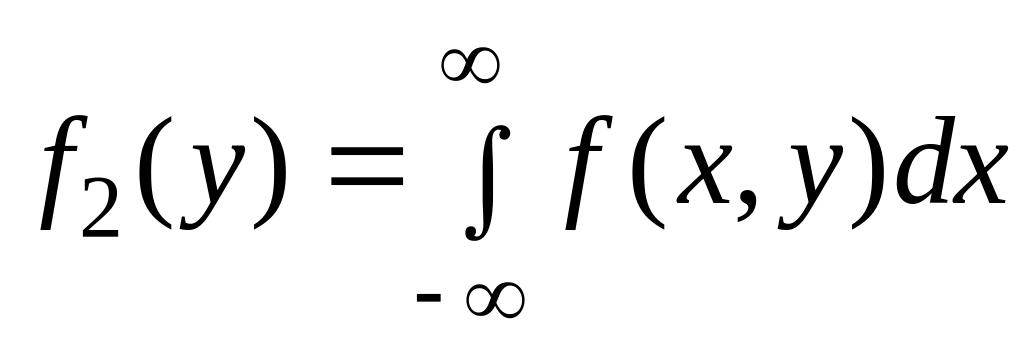где и – плотности распределения случайных величин и .

Условной плотностью распределения случайной величины при условии, что называют функцию ,

Аналогично определяют ,

Равенство называют теоремой умножения плотностей вероятности.

Случайные величины и называются независимыми, если для любых чисел , случайные события и независимы (см. стр.12).

Случайные величины независимы, если выполняется любое из условий:

.

или .

Для двумерных случайных величин вводят понятия начальных и центральных моментов, из которых наиболее часто используются математические ожидания , и дисперсии , составляющих, а также условные математические ожидания и корреляционный момент.

Условным математическим ожиданием для дискретного случайного вектора называется сумма:

Для двумерных непрерывных случайных величин условным математическим ожиданием называется интеграл:

Величина называется корреляционным моментом (ковариацией) двух случайных величин и .

Если – непрерывная двумерная случайная величина с плотностью распределения , то

,

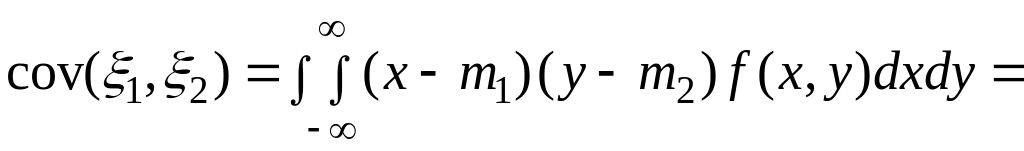
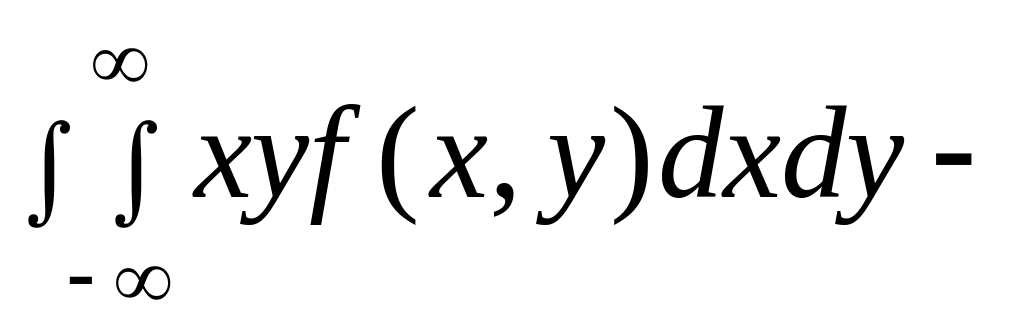
где .

Для дискретного случайного вектора

.

Величина 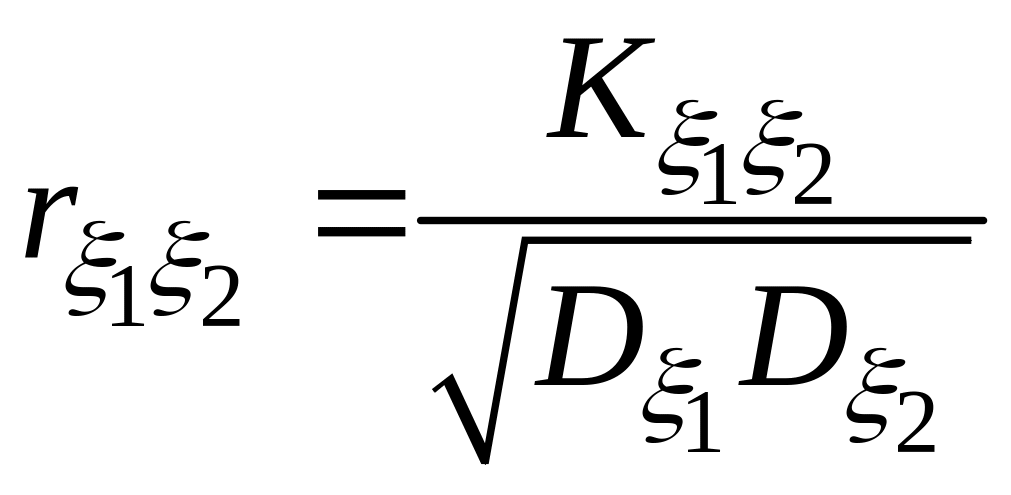называется коэффициентом корреляции случайных величин и .

Если , то случайные величины и называются некоррелированными.