8. Законы распределения и числовые характеристики случайных величин

Пусть (Ω, S, Р) – вероятностное пространство. Случайной величиной ξ будем называть функцию, действующую из пространства элементарных событий Ω в R¹, то есть ξ: Ω→R¹, удовлетворяющую следующему условию:

Для любых чисел , случайное событие

Так как вероятность Р определена на σ – алгебре S, то это требование означает, что для случайной величины всегда можно подсчитать вероятность ее попадания в любой интервал.

Функцией распределения вероятности случайной величины называется функция , .

Отметим, что знание функции распределения случайной величины достаточно для того, чтобы найти вероятности любых событий: , , .

Различают два основных типа случайных величин: дискретные случайные величины и непрерывные случайные величины. В приложениях встречаются случайные величины смешанного типа.

Случайные величины, принимающие дискретное множество значений, называются дискретными случайными величинами. Непрерывной называется случайная величина , функцию распределения которой , можно представить в виде

.

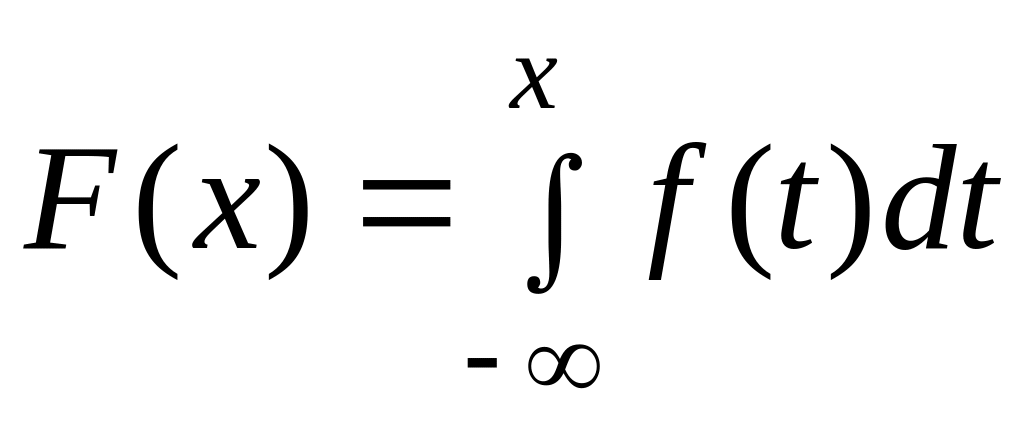Функция называется плотностью распределения вероятностей случайной величины .

Свойства функции распределения вероятности случайной величины

Функция распределения случайной величины есть неубывающая функция; , , , .

Для дискретных случайных величин функция распределения кусочно-постоянная, непрерывная слева, имеет разрывы 1 рода в точках , и величина скачка равна . Здесь все возможные значения, которые может принимать дискретная случайная величина,

Достаточно часто для дискретных случайных величин используют удобный описательный термин закон распределения. Это перечень возможных значений случайной величины и соответствующих им вероятностей.

Закон распределения дискретной случайной величины можно задать таблицей (рядом распределения), графически (многоугольник распределения), аналитически.

Свойства плотности распределения вероятности непрерывной случайной величины

1) .

2) .

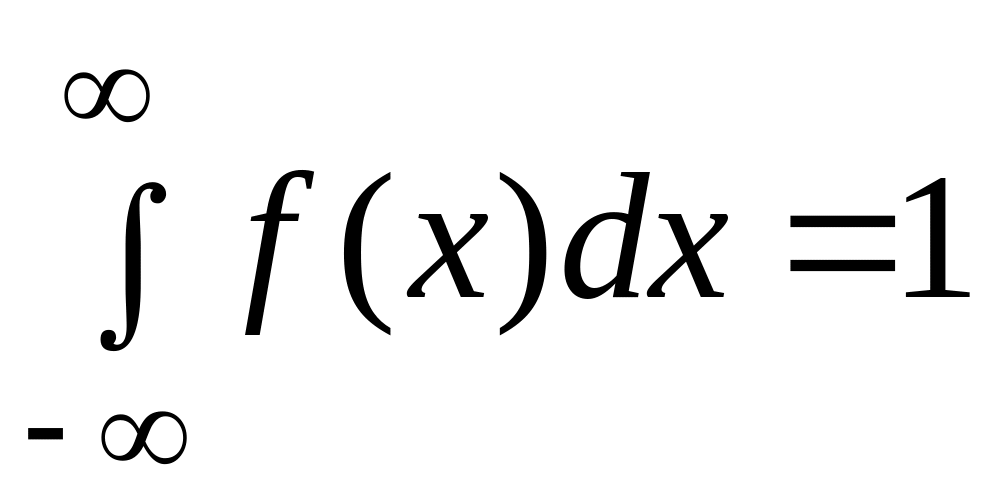3) в любой точке непрерывности .

4) .

Замечание. Для функции распределения дискретной случайной величины справедлива формула

,

где функция Хэвисайда. Дифференцируя последнее равенство, видим, что и для дискретной случайной величины можно ввести плотность распределения вероятности по формуле

.

Для случайных величин вводят понятия начальных и центральных моментов, из которых наиболее часто используются математическое ожидание и дисперсия.

Математическим ожиданием случайной величины называется число

(1)

Говорят, что математическое ожидание у случайной величины существует, если ряд (интеграл) (1) сходится абсолютно.

Дисперсией случайной величины называется число

.

Дисперсия вычисляется по формулам:

для дискретной случайной величины.

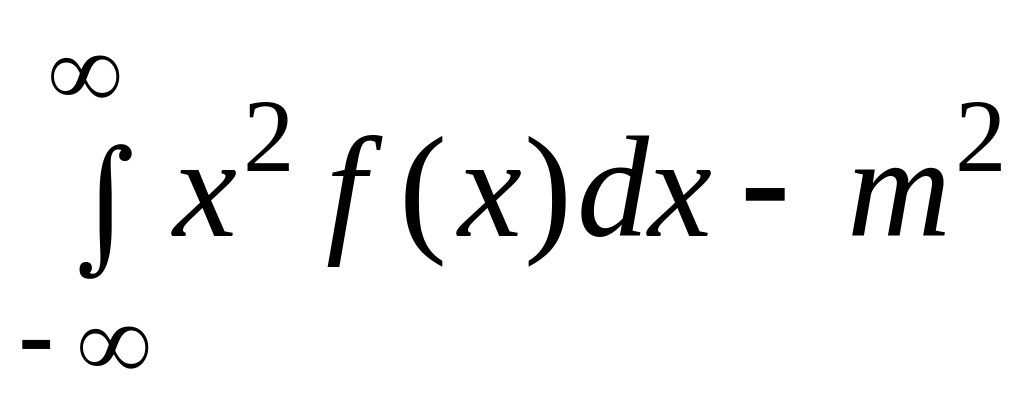для непрерывной случайной величины, где .

Рассеивание возможных значений случайной величины от её математического ожидания часто характеризуют средним квадратическим отклонением .

Существует достаточно большое число законов распределения дискретных и непрерывных величин, которые встречаются в приложениях. Параметры этих законов являются числовыми характеристиками случайных величин или же числовые характеристики выражаются через параметры законов распределения.