5. Предельная ошибка выборки.

В конкретной выборке действительная ошибка может быть больше средней, меньше средней или равна средней. Каждое из этих расхождений имеет определенную вероятность.

Предельная ошибка выборки – это максимальное различие между выборочной и генеральной характеристикой, гарантируемое с определенной вероятностью.

где t – нормированное отклонение, зависящее от вероятности, определяемое как аргумент интегральной функции Лапласа Ф(t). Определение предельной ошибки выборки основано на теореме Чебышева –Ляпунова.

Теорема Чебышева-Ляпунова:

С вероятностью сколь угодно близкой к единице можно утверждать, что при достаточно большом объеме выборки и ограниченной дисперсии выборочная характеристика будет очень мало отличаться от генеральной характеристики.

З начение этой функций находиться в таблице, поэтому, зная вероятность P =Ф(t), можно определить аргумент t.

Наиболее часто используемые значения приведем в таблице:

Р(t)	0,683	0,95	0,954	0,99	0,997
t	1	1,96	2	2,58	3

Чем больше вероятность, с которой гарантируются результаты, тем больше будет предельная ошибка и менее надежные результаты выборки. Поэтому в экономических исследованиях используется Р=0,95 и Р=0,954.

6. Распределение результатов выборки на генеральную совокупность

Конечным итогом выборочного обследования является оценка неизвестных генеральных характеристик на основе данных выборки.

По этой оценке строится доверительный интервал для генеральной средней

и генеральной доли.

Ошибка выборки зависит не только от вероятности, но и от того, как было организовано выборочное обследование.

Выделим основные этапы выборочного обследования:

1. определение объекта исследования;

2. постановка цели и задач;

3. определение процедуры отбора, проведение отбора единиц в выборку;

4. подготовка кадров и инструментария;

5. сбор данных;

6. определение выборочных характеристик, ошибок выборки;

7. оценка доверительных интервалов;

8. о 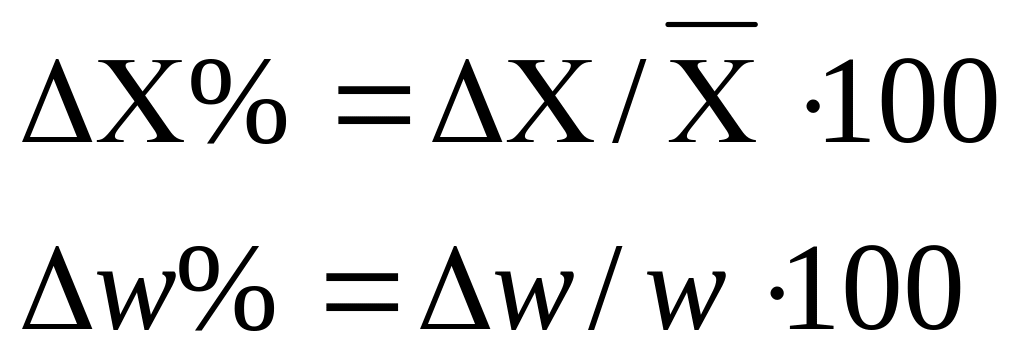ценка возможностей распространения результатов на генеральную совокупность. Для этого определяют относительные ошибки выборки:

Если эти ошибки не превышают заранее заданной величины, то результаты можно распространить на генеральную совокупность, если превышает, то изменить процедуру отбора или методы ремонта выборки.

9. Распространение результатов. Для этого применяются следующие способы:

1. Прямой пересчет, т.е. границы доверительного интервала умножаются на объем генеральной совокупности.

2. Способ поправочных коэффициентов – используется в тех случаях, когда корректируются данные сплошного обследования. По выборке рассчитывается поправочный коэффициент, и данные сплошного обследования исправляются на этот коэффициент.

7. Определение необходимой численности выборки.

При проведении выборочного обследования возникает вопрос, сколько нужно отобрать единиц в выборку, чтобы результаты обследования удовлетворяли заранее заданным величинам, т.е. предельная ошибка не превышала определенного значения. Для определения необходимой численности выборки применяются формулы, которые выводятся из предельной ошибки.

Возьмем собственно-случайный повторный отбор:

______

∆_x = t∙μ_x = t∙√S_x² / n => n = t²· S_x²

∆_x²

Для бесповторного отбора:

___________

∆_x = t·√S_x / n·(1-n/N) => t²·N·S_x²

n = ____________

∆_x²·N + t²· S_x²

Для других способов отбора формулы необходимой численности выборки аналогичны, изменяется только дисперсия.

Значения дисперсии при определении необходимой численности выборки достаточно часто бывает неизвестно. В этом случае ее определяют:

1. из предыдущего обследования на данную тему;

2. рассчитывают приближенно S_x²≈(R/6)² по пробному обследованию малого количества единиц;

3. неизвестную дисперсию для доли берут равной 0,25.

Области применения выборочного метода обследования.

В настоящее время выборочный метод сбора данных является одним из наиболее часто используемых. Выборочное наблюдение используется для:

1. статистического оценивания и проверки различных гипотез;

2. при контроле технологических процессов и показателей качества продукции;

3. при различных отраслевых обследованиях;

4. при решении задач в сфере предпринимательства.

5. 

Пример: Имеются данные выборочного собственно-случайного бесповторного обследования 30% работников коммерческого банка об их стаже работы. Результаты обследования представлены в таблице.

Стаж работы, лет	До 3	3-5	5-7	7-9	Свыше 9	Итого
Число работников, чел.	10	48	28	10	4	100

С вероятностью 0,997 определить возможные пределы среднего стажа работы по всем работникам банка, а также возможные пределы для доли работников банка, имеющих стаж работы менее 5 лет.

Решение: 1 Для расчетов построим расчетную таблицу

Стаж, лет	Число работ., fi	Середина xi	xi*fi	_ (xi – x)	_ (xi – x)2	_ (xi – x)2*fi
До 3	10	2	20	- 3	9	90
3-5	48	4	192	- 1	1	48
5-7	28	6	168	1	1	28
7-9	10	8	80	3	9	90
Свыше 9	4	10	40	5	25	100
Итого	100	-	500	-	-	356

С редний стаж работников равен

Д исперсия равна

Средн­­еквадратическое отклонение равно  = ² = 3,56 = 1,887 лет.

Определим ошибки выборки. Так как вероятность Р= 0,997, то коэффициент доверия t = 3. Рассчитаем выборочную долю для признака – стаж работы менее 5 лет. Так как данный стаж работы имеют 1 и 2 группы работников в выборке, то w = m/n = (10+48)/100 = 0.58. Дисперсия выборочной доли ²_w = w*(1 – w) = 0,58*0,42 =0,2434.

Определим предельную ошибку выборки для среднего

О пределим предельную ошибку выборки для доли

Построим доверительный интервал для среднего.

П остроим доверительный интервал для выборочной доли

В ывод 2. С вероятностью 0,997 можно утверждать, что средний стаж работы всех работников банка находится в пределах от 4,526 до 5,474 лет, а доля всех работников банка, имеющих стаж работы менее 5 лет, находится в пределах от 45,6% до 70,4%.

7