1. Постановка задачі
Нехай інвестор свій капітал в сумі К вкладає в 3 акції (К1, К2, К3). Відома динаміка цін цих акцій за місяць на фондовому ринку. Розрахувати прибутковість сподіваної норми прибутку і ризик для трьох акцій; дати характеристику систематичного ризику для кожної акції; розрахувати сподівану норму портфелю цінних паперів і його ризик, а також оптимізувати портфель цінних паперів за моделями Марковіца.
2. Розрахунок прибутковості, сподіваної норми прибутку, дисперсії і стандартного відхилення для кожної акції.
Для визначення ціни акції певного періода застосуємо функію «Анализ данных→Генерация случайных чисел (66; 16)» в програмі Microsoft Excel і отримали такі дані:
Дні |
Ціна ак 1 |
Ціна ак 2 |
Ціна ак 3 |
1 |
61 |
46 |
70 |
2 |
86 |
85 |
94 |
3 |
31 |
62 |
84 |
4 |
49 |
55 |
39 |
5 |
36 |
50 |
54 |
6 |
32 |
57 |
60 |
7 |
68 |
60 |
61 |
8 |
60 |
87 |
65 |
9 |
63 |
58 |
98 |
10 |
80 |
104 |
56 |
11 |
93 |
40 |
75 |
12 |
80 |
97 |
65 |
13 |
58 |
77 |
60 |
14 |
78 |
43 |
52 |
15 |
42 |
60 |
65 |
16 |
66 |
61 |
101 |
17 |
38 |
54 |
25 |
18 |
89 |
46 |
56 |
19 |
78 |
73 |
80 |
20 |
76 |
44 |
48 |
21 |
77 |
71 |
51 |
22 |
62 |
68 |
75 |
23 |
68 |
51 |
96 |
24 |
74 |
67 |
79 |
25 |
80 |
56 |
51 |
26 |
84 |
47 |
41 |
27 |
77 |
76 |
101 |
28 |
89 |
87 |
68 |
29 |
66 |
73 |
66 |
30 |
49 |
38 |
79 |
Для розрахунку прибутковості кожної акції застосуємо таку формулу:
,
Де С(t) – ціна акції t-го періоду; С(t-1) – ціна акції попереднього періоду.
Виконавши розрахунки, отримаємо такі значення:
Прибутковість |
||
R1 |
R2 |
R3 |
41,224 |
86,960 |
34,076 |
-64,058 |
-26,910 |
-10,893 |
56,499 |
-11,720 |
-53,361 |
-25,021 |
-8,368 |
37,663 |
-11,897 |
13,017 |
11,024 |
112,243 |
5,691 |
2,071 |
-11,857 |
45,435 |
6,364 |
4,903 |
-33,942 |
50,932 |
26,704 |
79,984 |
-43,087 |
15,945 |
-61,348 |
34,404 |
-13,121 |
140,544 |
-13,368 |
-28,365 |
-20,579 |
-7,346 |
35,583 |
-44,151 |
-12,445 |
-46,680 |
40,335 |
24,857 |
59,525 |
1,068 |
54,416 |
-42,633 |
-10,882 |
-75,514 |
133,898 |
-16,033 |
124,336 |
-12,381 |
61,382 |
44,022 |
-3,317 |
-40,041 |
-39,810 |
2,081 |
61,547 |
5,845 |
-19,401 |
-4,297 |
47,019 |
9,775 |
-24,492 |
28,339 |
8,173 |
30,591 |
-17,555 |
8,126 |
-16,887 |
-35,380 |
4,997 |
-16,186 |
-19,854 |
-7,637 |
62,917 |
146,704 |
15,144 |
13,971 |
-33,057 |
-25,891 |
-15,661 |
-3,267 |
-25,603 |
-48,671 |
20,828 |
Щоб розрахувати сподівану норму прибутку, використаємо наступну формулу:
, але в нашій задачі
нам не дана ймовірність до t-го
періоду (стану), тобто Рt.
Тому будемо використовувати таку формулу
для обчислення:
.
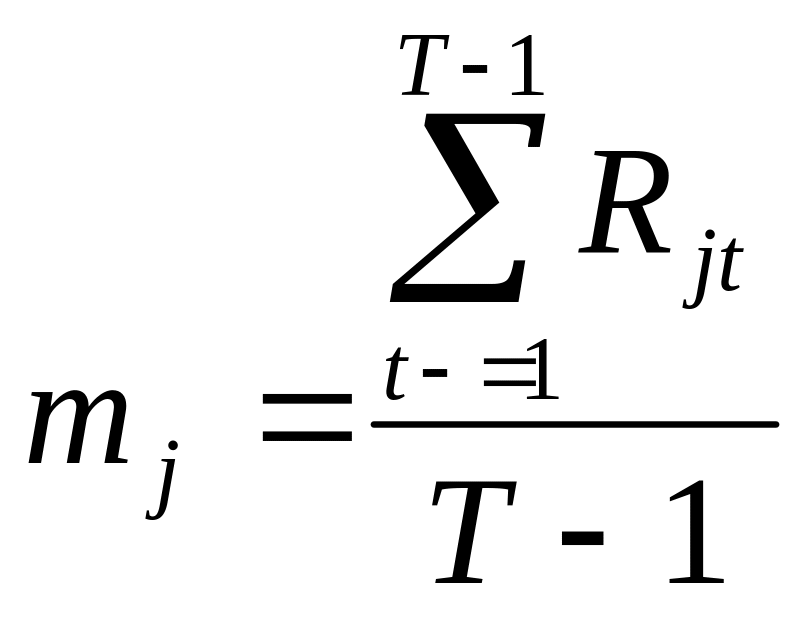Також треба зауважити на те, що mj
завжди повинна бути величиною додатною.
В нашій задачі mj
набуває
таких значень:
Норма прибутку |
||
m1 |
m2 |
m3 |
6,792 |
8,389 |
10,619 |
Дисперсію можна визначити за такою формулою
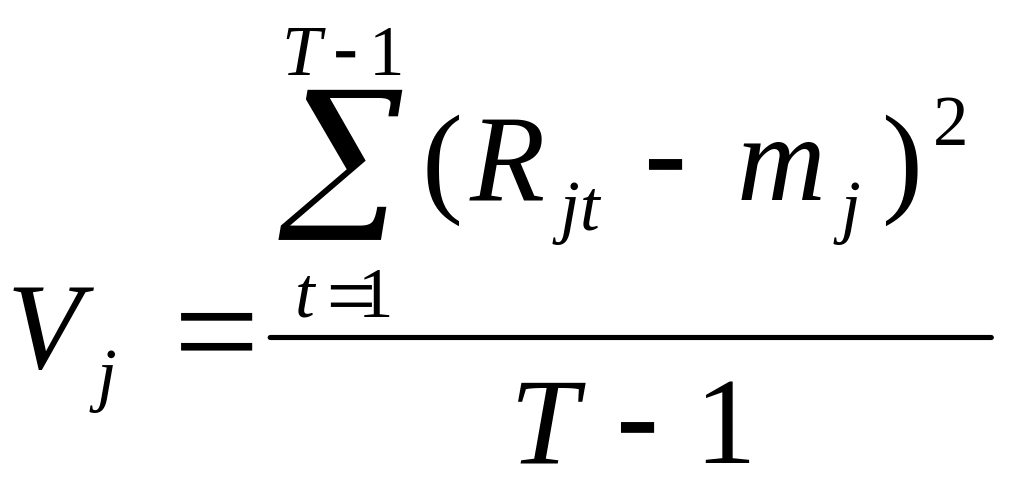
R1-m1 |
R2-m2 |
R3-m3 |
|
(R1-m1)^2 |
(R2-m2)^2 |
(R3-m3)^2 |
34,432 |
78,571 |
23,457 |
|
1185,556 |
6173,476 |
550,220 |
-70,849 |
-35,299 |
-21,512 |
|
5019,637 |
1246,027 |
462,772 |
49,708 |
-20,109 |
-63,980 |
|
2470,862 |
404,382 |
4093,489 |
-31,813 |
-16,757 |
27,043 |
|
1012,040 |
280,791 |
731,343 |
-18,688 |
4,629 |
0,404 |
|
349,260 |
21,424 |
0,163 |
105,451 |
-2,698 |
-8,549 |
|
11119,879 |
7,278 |
73,077 |
-18,649 |
37,046 |
-4,255 |
|
347,775 |
1372,428 |
18,108 |
-1,889 |
-42,331 |
40,312 |
|
3,568 |
1791,928 |
1625,083 |
19,912 |
71,595 |
-53,707 |
|
396,503 |
5125,901 |
2884,401 |
9,154 |
-69,737 |
23,785 |
|
83,791 |
4863,283 |
565,713 |
-19,913 |
132,155 |
-23,987 |
|
396,531 |
17465,021 |
575,384 |
-35,157 |
-28,968 |
-17,965 |
|
1236,024 |
839,131 |
322,749 |
28,791 |
-52,540 |
-23,065 |
|
828,924 |
2760,462 |
531,983 |
-53,471 |
31,946 |
14,238 |
|
2859,174 |
1020,570 |
202,713 |
52,733 |
-7,321 |
43,796 |
|
2780,792 |
53,601 |
1918,130 |
-49,425 |
-19,271 |
-86,133 |
|
2442,801 |
371,359 |
7418,892 |
127,107 |
-24,422 |
113,717 |
|
16156,123 |
596,430 |
12931,488 |
-19,173 |
52,994 |
33,403 |
|
367,594 |
2808,329 |
1115,734 |
-10,109 |
-48,430 |
-50,429 |
|
102,190 |
2345,431 |
2543,131 |
-4,710 |
53,158 |
-4,774 |
|
22,188 |
2825,818 |
22,792 |
-26,193 |
-12,685 |
36,400 |
|
686,066 |
160,921 |
1324,940 |
2,983 |
-32,880 |
17,719 |
|
8,900 |
1081,123 |
313,977 |
1,382 |
22,202 |
-28,174 |
|
1,909 |
492,930 |
793,775 |
1,335 |
-25,275 |
-46,000 |
|
1,782 |
638,843 |
2115,964 |
-1,795 |
-24,575 |
-30,474 |
|
3,222 |
603,924 |
928,654 |
-14,428 |
54,528 |
136,085 |
|
208,173 |
2973,344 |
18518,991 |
8,353 |
5,582 |
-43,676 |
|
69,767 |
31,162 |
1907,618 |
-32,683 |
-24,049 |
-13,887 |
|
1068,154 |
578,375 |
192,846 |
-32,395 |
-57,060 |
10,209 |
|
1049,419 |
3255,836 |
104,218 |
Дисперсія |
||
V1 |
V2 |
V3 |
1802,710 |
2144,466 |
2234,081 |
Середнє квадратичне відхилення – це є квадрат з дисперсії:
,
Сигма |
||
|
|
|
42,458 |
46,308 |
47,266 |