3.Лабораторная работа №2. Моделирование исполнительного электродвигателя.
Цель работы: получить параметры механической характеристики электродвигателя постоянного тока, моделируемого в среде программного пакета MatLAB/Simulink.
Программа работы:
Открыть файл Labrab2.mdl.
Установить исходные параметры элементов модели в соответствии с заданным вариантом (используются варианты, перечисленные в лабораторной работе 1).
Запустить моделирование.
По графику X Y Plot оценить скорость холостого хода и пусковой момент электродвигателя.
Оформить отчёт.
Пример:
Для набора параметров («DC Voltage Source» = 240 В, «DC Voltage Source1» = 240 В, вариант электродвигателя (Preset model) = 1) имеем результат
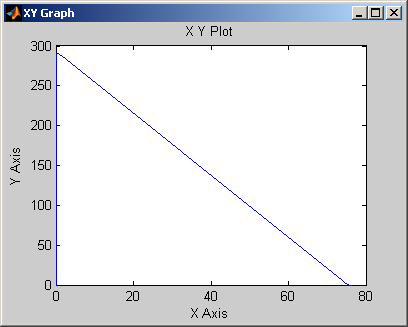
, по графику определяем скорость холостого хода 280-290 рад/сек и пусковой момент 75-77 Н*м.
4.Лабораторная работа №3. Моделирование одноконтурной системы автоматического управления.
Цель работы: получить представление об одноконтурных САУ на примере моделируемой системы стабилизации скорости.
Программа работы:
Открыть файл Labrab3.mdl.
Установить исходные параметры элементов модели в соответствии с заданным вариантом (используются варианты, перечисленные в лабораторной работе 1).
Исходное состояние переключателей:
Запустить моделирование.
На графике OutData показана зависимость частоты вращения от момента нагрузки на протяжении времени моделирования:
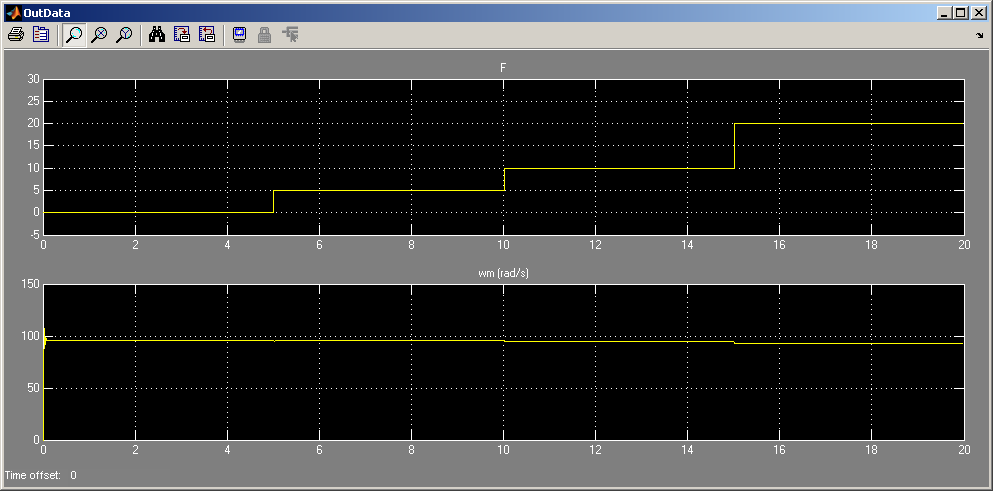
На графике OutData1 показана зависимость ошибки стабилизации частоты вращения от момента нагрузки на протяжении времени моделирования (в примере – 5-8 рад/сек):
Включить цепь обратной связи по возмущению (MS_D3).
При необходимости откорректировать коэффициент усиления D3 так, чтобы скомпенсировать влияние возмущения на стабилизируемую частоту вращения:
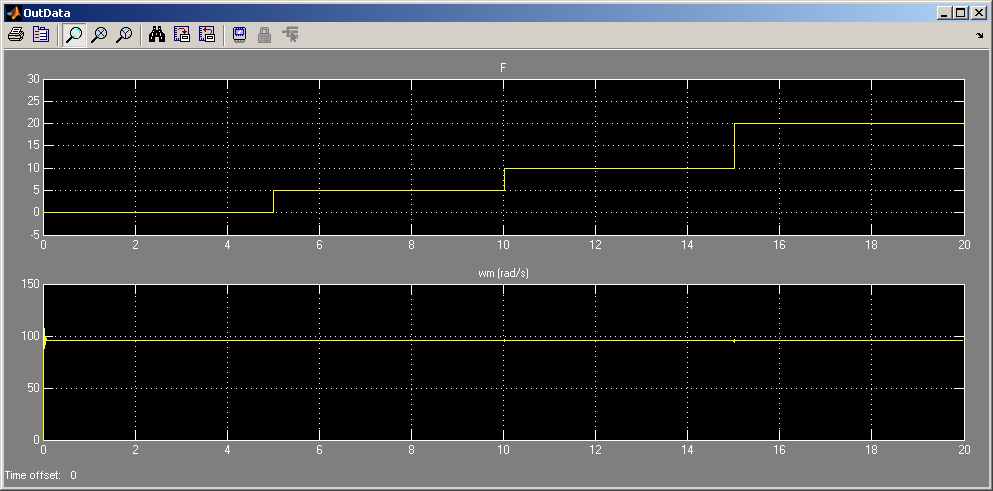
Следует иметь в виду, что возможны энергетические ограничения, из-за которых на больших моментах нагрузки не удастся осуществить стабилизацию скорости во всём диапазоне.
Оценить статическую ошибку системы (в примере – 4-5 рад/сек).
Повторить п.п. 4, 5 для подключения обратной связи по возмущению до усилителя D4 (при необходимости откорректировать коэффициент усиления D1). Этот пункт иллюстрирует правила эквивалентных преобразований структурных схем систем автоматического управления.
Отключить обратную связь по возмущению и подключить интегрирующее звено. Убедиться в практическом отсутствии статической ошибки полученной астатической системы (при необходимости следует откорректировать коэффициенты усиления D4, D5).
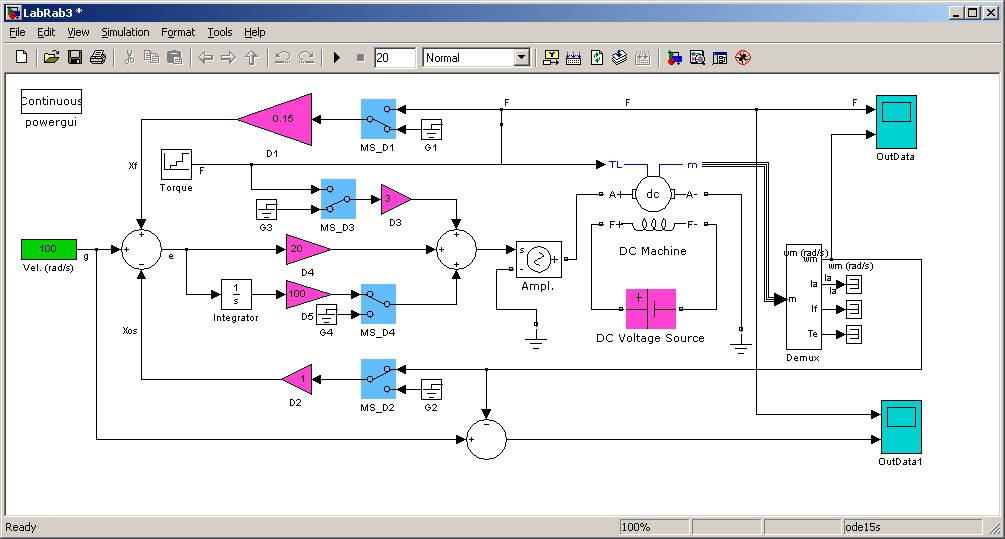
Оформить отчёт, в котором указать результаты, полученные в п.п. 3, 5, 7.
5.Лабораторная работа №4. Моделирование двухконтурной системы автоматического управления.
Цель работы: получить представление о двухконтурных САУ на примере моделируемой системы стабилизации углового положения.
Программа работы:
Открыть файл Labrab4.mdl.
Установить исходные параметры элементов модели в соответствии с заданным вариантом (используются варианты, перечисленные в лабораторной работе 1).
Исследование простейшей статической одноконтурной системы.
Исходное состояние переключателей:
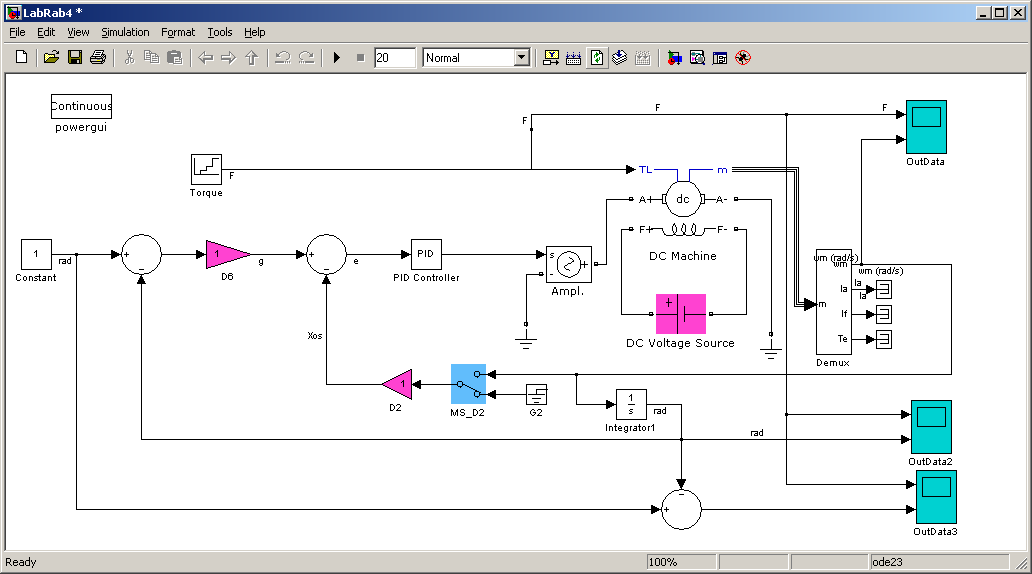
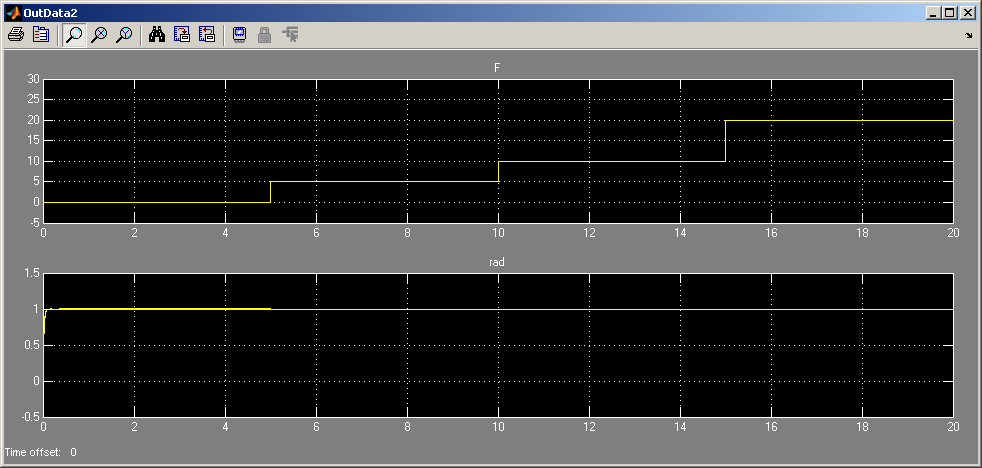
В окне OutData2 можно наблюдать зависимость углового положения от момента нагрузки. Заданный угол составляет 1 рад. В окне OutData3 можно наблюдать зависимость ошибки системы по угловому положению от момента нагрузки.
Следует установить следующие начальные параметры PID Controller-а:
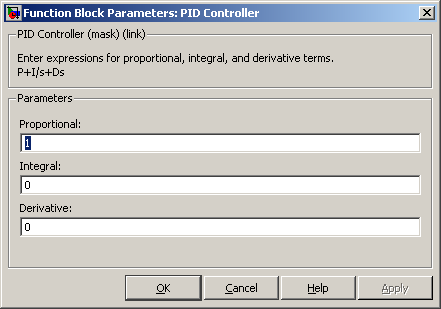
Далее следует увеличивать коэффициент усиления (параметр «Proportional») до возникновения автоколебаний системы, и установить его как можно большим при отсутствии автоколебаний. Это соответствует максимально возможному коэффициенту усиления для простейшей одноконтурной системы, замкнутой по угловому положению.
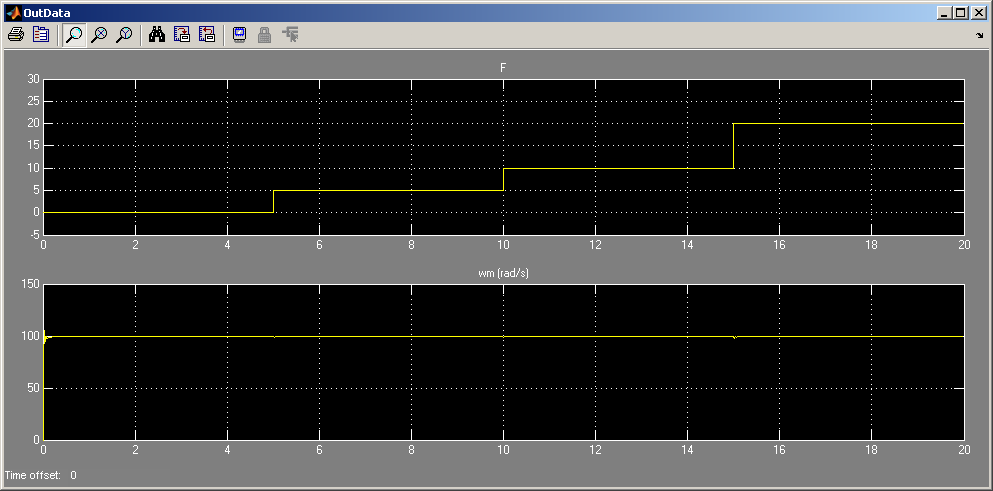
В примере выбрано значение 80, при этом видно, что система имеет очень большую ошибку и плохой вид переходного процесса:
Исследование простейшей астатической одноконтурной системы.
Следует включить интегратор PID Controller-а, получая тем самым астатическую систему. Практически достаточно снизить пропорциональный коэффициент усиления в 2 раза по сравнению с полученным в предыдущем пункте, и затем увеличивать параметр Integral до получения сравнительно небольшой ошибки стабилизации углового положения.
Начальные коэффициенты PID Controller-а для примера:
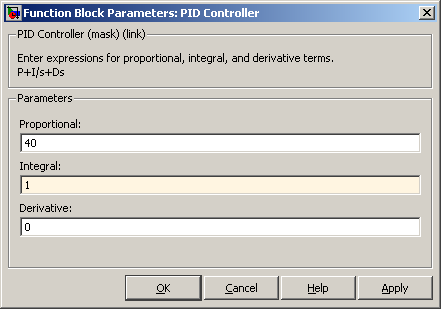
Конечные коэффициенты PID Controller-а для примера, и результат:
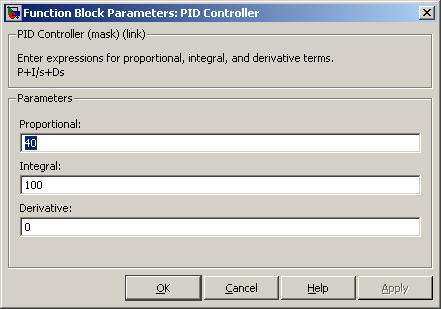
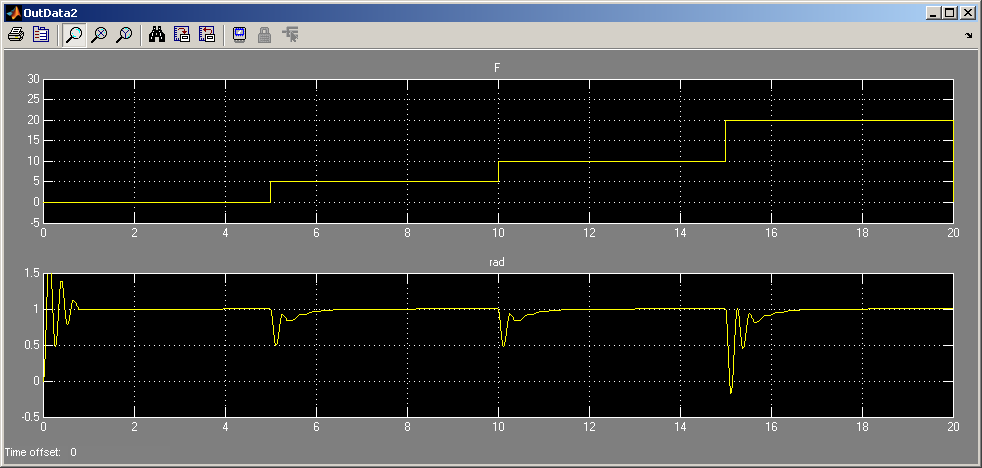
Как видно, ошибку можно существенно уменьшить, но переходной процесс оставляет желать лучшего.
Исследование двухконтурной системы с жёсткой тахометрической обратной связью.
Исходное состояние переключателей:
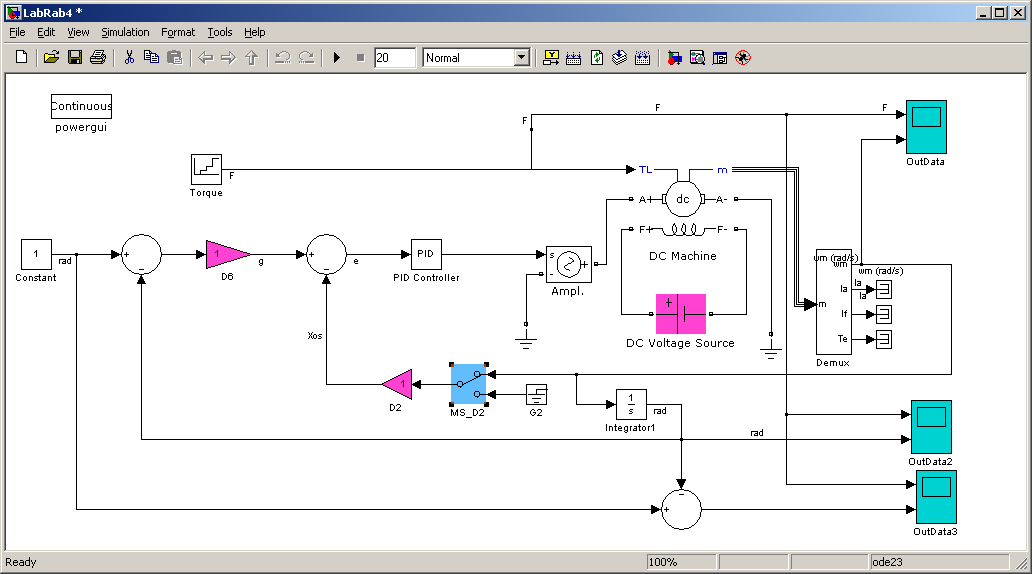
Начальные коэффициенты PID Controller-а:
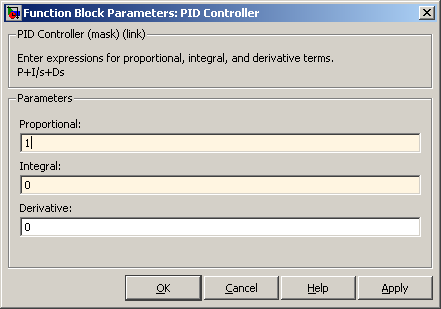
Далее следует увеличивать пропорциональный коэффициент усиления до получения малой статической ошибки (для примера):
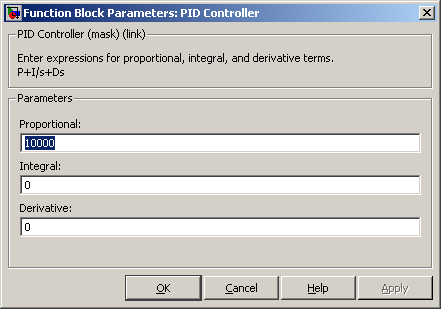
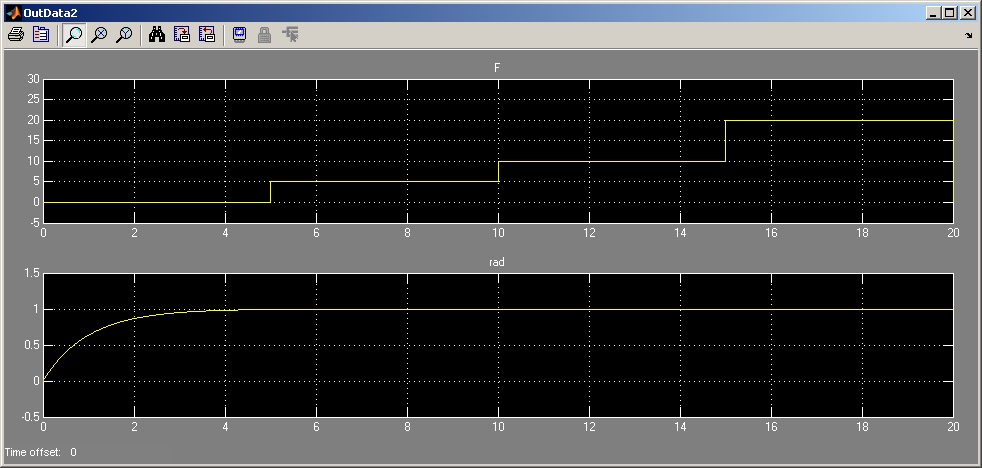
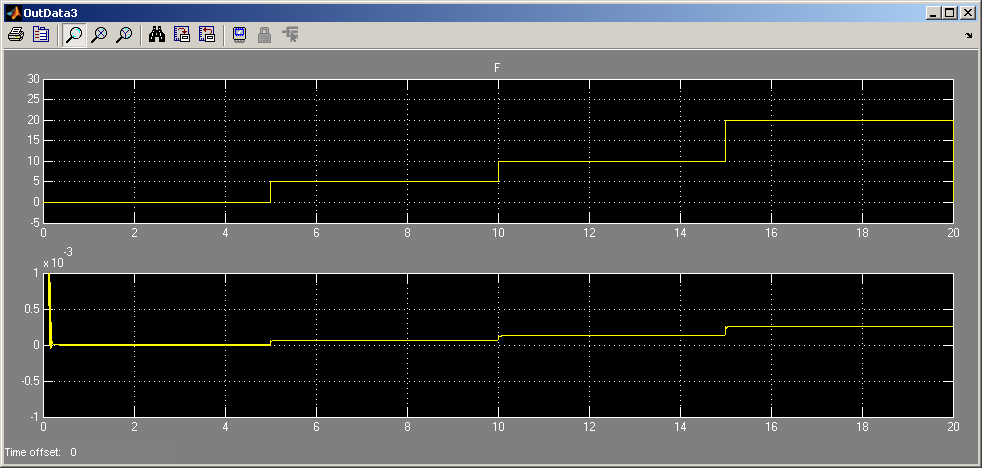
И наконец, снизить полученный коэффициент в 2 раза и увеличить коэффициент усиления D6 до получения стабильного, но короткого переходного процесса:
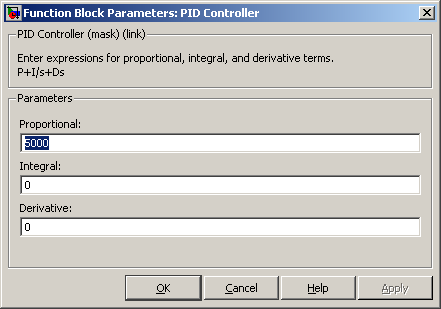
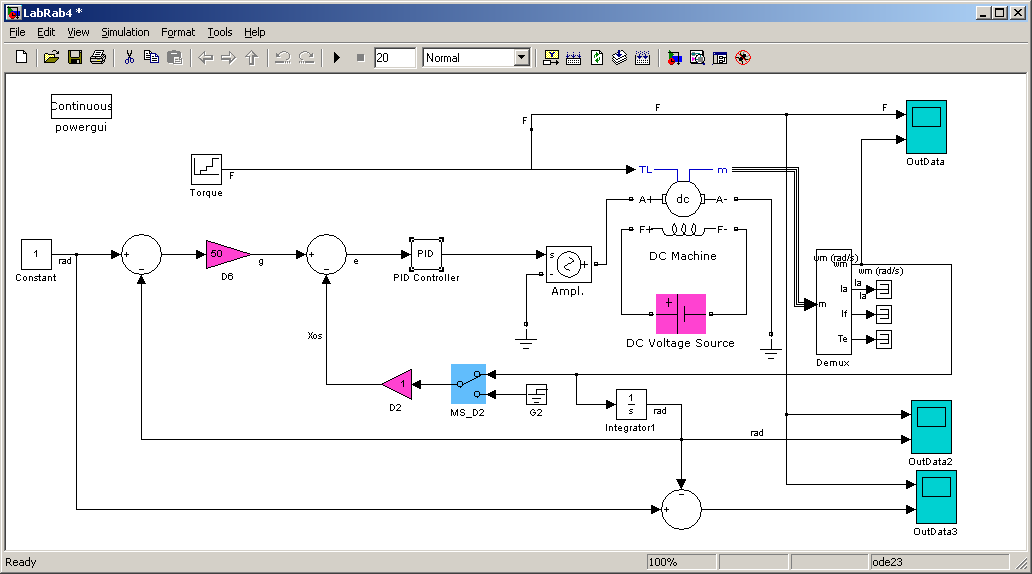
В окне OutData3 можно увидеть, что ошибка системы мала (< 0,0005 рад для примера):
Оформить отчёт, в котором указать результаты, полученные в п.п. 3, 4, 5.
