3.Создание субблока.
Для того, чтобы создать субблок в среде Electronics Workbench , необходимо:
1.Выделить схему, которую вы хотите объединить в субблок (схема не должна содержать такие блоки, как Word Generator и Logic Analyzer)
2.На панели меню ,в разделе Circuit воспользоваться функцией Create Subcircuit
3.В появившемся меню необходимо дать название субблоку и нажать на кнопку Copy from Circuit.
4.Полученный субблок можно использовать для дальнейшего проектирования
Рисунок №4 «Субблок 4→1»
4.Создание мультиплексоров ms 8→1 и ms 16→1 на основе ms 4→1.
1.Ms 8→1 на основе ms 4→1
1)Запишем его уравнение в виде двух строк:
В
первой строке адресная переменная a2
встречается только с инверсией,
а во второй – только без инверсии. Вынося
за скобки переменную
в первой строке и a2
во второй, получим:
(1)
В выражении (1) в скобках записаны уравнения двух мультиплексоров MS 4–1 с общим адресом, представленным двумя младшими переменными a1, a0.
2) Схема:
Проверим правильность работы схемы с использованием 8 ключей и набором, которые они будут представлять 11000111.
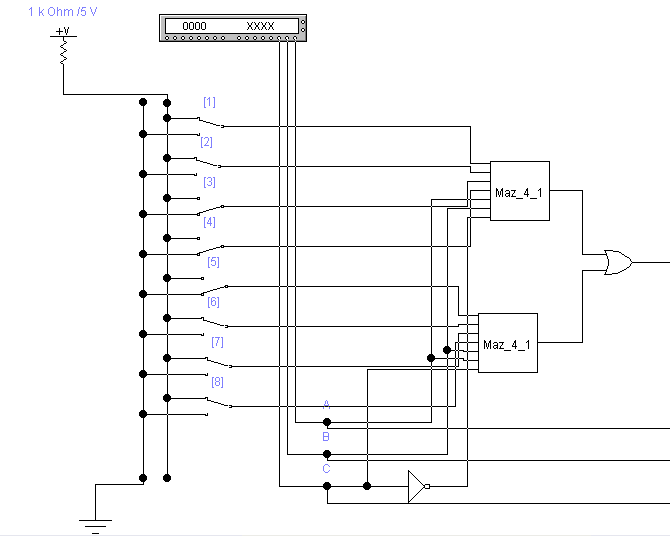
Рисунок №5 «MS 8→1»
Временные диаграммы:
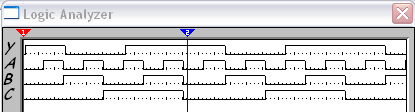
Рисунок №6 «Временная диаграмма MS 8→1»
Сложность схемы:С=79. Время формирования сигнала :T=6tз
2.Ms 16→1 на основе ms 4→1
1)Запишем уравнение для этого мультиплексора в виде матрицы из четырех строк и четырех столбцов (разрядность адреса для MS 16–1 равна четырем):
В этом выражении имеют единое представление в каждой строке две старшие адресные переменные, а в каждом столбце – две младшие.
2)Схема: Для проверки, подадим на входы последовательность 1111110000000000:
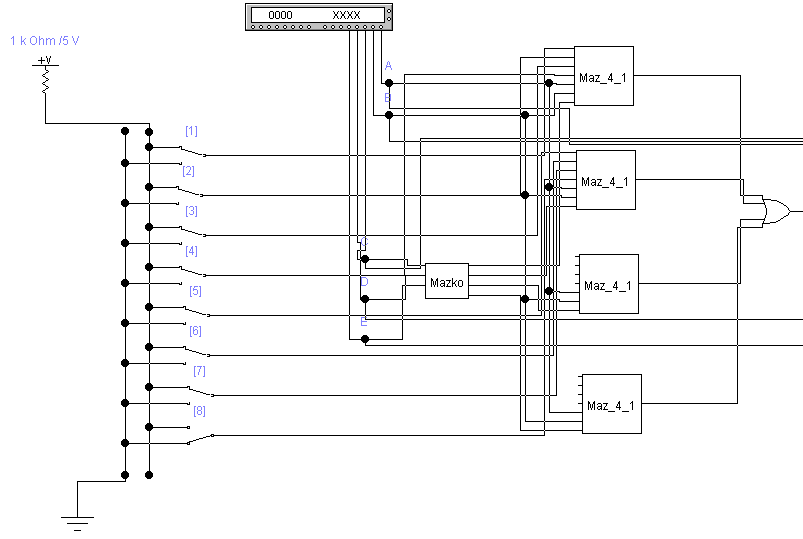
Рисунок №7 «MS 16→1»
Временные диаграммы:
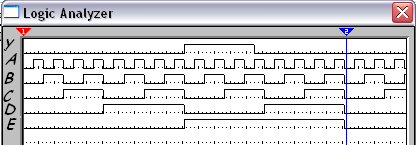
Рисунок №8 «Временная диаграмма MS 16→1»
Сложность схемы: С=181. Время формирования результата: Т=8tз
Вывод №2:метод каскадирования позволяет построить мультиплексор любой разрядности, она имеет очевидный недостаток – существенное возрастание задержек распространения сигналов в последовательно включенных ярусах мультиплексоров.
5.Реализация логических функций с помощью мультиплексора.
Ее можно реализовать на мультиплексоре, имеющем n управляющих и 2n информационных входов. В этом случае каждой комбинации значений аргументов соответствует единственный информационный вход мультиплексора, на который подается соответствующее значение функции.
1.Функция задана набором единичных значений – 0,1,4,6.
СДНФ:
Схема:
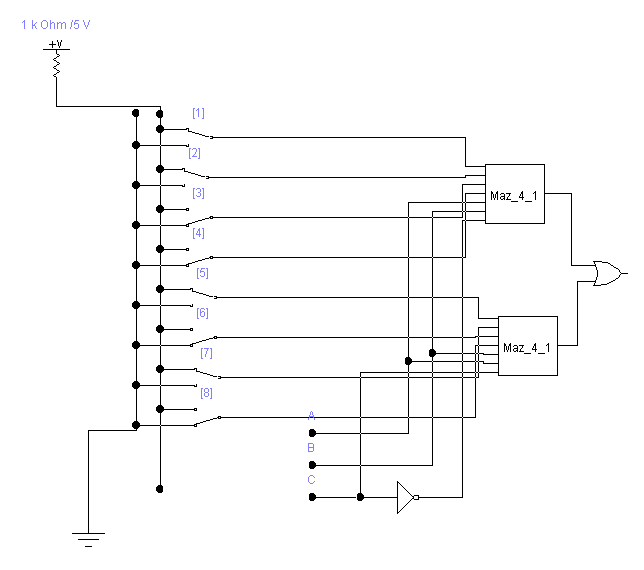
Рисунок №9 «Логическая функция 1»
Временные диаграммы:
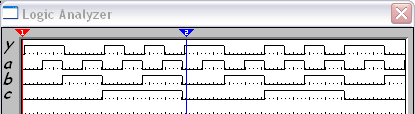
Рисунок №10 «Временная диаграмма лф1»
Сложность схемы:С=79, Время формирования результата : T=6tз
2.Функция задана частично. Известны лишь часть наборов: единичные наборы функции – 2,3,7,8, 10 ;нулевые наборы функции – 0,5,6,12,13.
СДНФ:
СКНФ:
Схема:
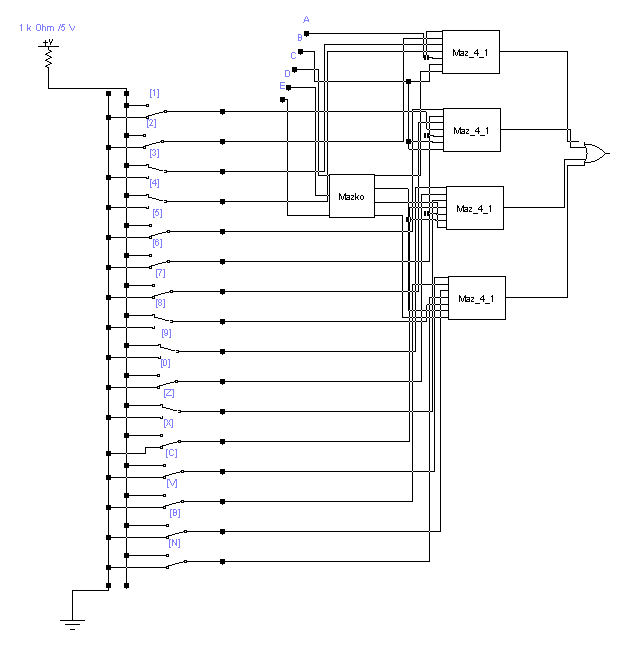
Рисунок №11 «Логическая функция 2»
Временные диаграммы:
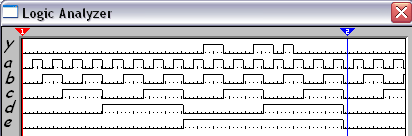
Рисунок №12 «Временная диаграмма лф2»
Сложность схемы:C=181.Время формирования результата : Т=8tз
3.Функции заданы наборами единичных значений:
F1(d,c,b,a) – 0,2,4,5,11,12,13; F2 (d,c,b,a)– 1,3,4,5,8,11,12,13 ; F3 (d,c,b,a)– 0,2,3,11,13,15
F1:
СДНФ -
F2:
СДНФ -
F3:
СДНФ -
Схема:
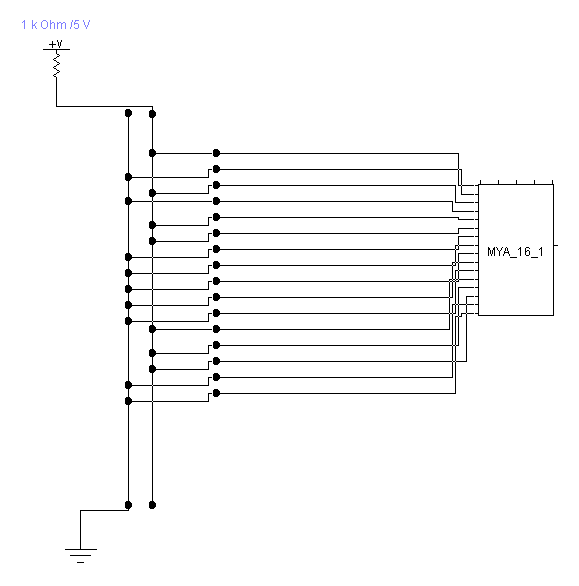
Рисунок №13 «Логическая функция F1»
Временные диаграммы:
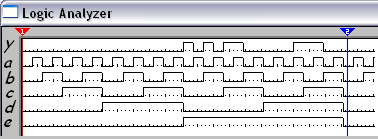
Рисунок №14 «Временная диаграмма F1»
Сложность:С=171. Время формирования результата: Т=8tз
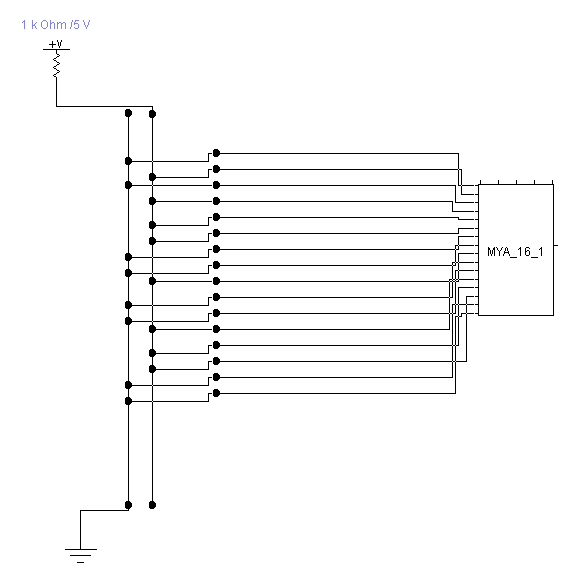
Рисунок №15 «Логическая функция F2»
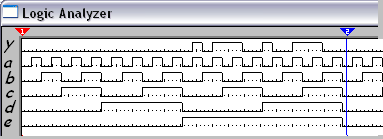
Рисунок №16 «Временная диаграмма F2»
Сложность:С=171. Время формирования результата: Т=8tз
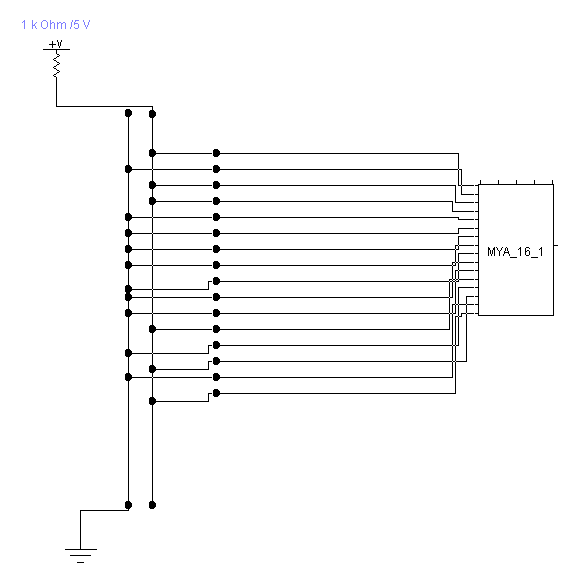
Рисунок №17 «Логическая схема F3»
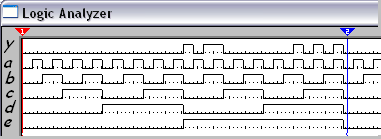
Рисунок №18 «Временная диаграмма F3»
Сложность:С=171. Время формирования результата: Т=8tз
Вывод №3: если количество логических переменных n, от которых зависит реализуемая логическая функция, совпадает с разрядностью адресной части мультиплексора, то эти переменные подаются на адресные входы мультиплексора (старшая переменная - на старший адресный вход), а на информационные входы мультиплексора MS 2n–1 – константы 0 и 1 в соответствии с таблицей истинности реализуемой функции.