
- •1. Алгебраические структуры.
- •2. Определение многочлена. Операции над многочленами.
- •3. Кольцо многочленов над областью целостности.
- •4. Деление многочленов с остатком. Разложение многочлена на множители.
- •5. Наибольший общий делитель. Алгоритм евклида.
- •6. Кратность корня и производная многочлена.
- •7. Разложение дробей на простейшие.
- •Задания к типовому расчету
- •Библиографический список
- •Содержание
- •190031, СПб, Московский пр., 9.
6. Кратность корня и производная многочлена.
Определение 1.
Корень
многочлена
имеет кратность
![]() если
если
![]() и
и
![]() ,
,
![]() .
Корни кратности 1 называют простыми,
остальными
кратными.
.
Корни кратности 1 называют простыми,
остальными
кратными.
Для того чтобы узнать, кратен корень или нет, бывает полезным понятие производной многочлена. Если рассматривать многочлен с числовыми коэффициентами как функцию, то это понятие совпадает с обычной производной, определяемой в анализе. Следовательно, все свойства производной сохраняются у производной многочлена.
Теорема
1. Простой
корень многочлена
не является корнем его производной;
кратный корень кратности
![]() является корнем производной, и кратность
его в производной равна
является корнем производной, и кратность
его в производной равна
![]() .
.
Теорема
2. Для того
чтобы число
было корнем кратности
многочлена
необходимо и достаточно, чтобы
![]() и
и
![]() .
.
Всякий многочлен можно представить в виде
![]() ,
,
т.е. разложить его по степеням линейного двучлена . Такое разложение однозначно и дается формулой Тейлора
![]() .
.
ПРИМЕРЫ:
1. Найти
кратность корня
в многочлене
![]() ,
,
![]() .
.
Решение: Для решения задачи воспользуемся схемой Горнера:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
– первый |
|
|
|
|
|
|
|
|
|
– второй |
|
|
|
|
|
|
|
|
|
– третий |
|
|
|
|
|
|
|
|
|
– четвертый |
|
|
|
|
|
|
|
|
|
|
Искомая кратность равна .
2. Найти
при каких
и
![]() многочлен
многочлен
![]() делится на
делится на
![]() .
.
Решение:
Условие
задачи означает, что
– является корнем кратности не меньшей
,
что равносильно утверждению
![]() .
.
Найдем
![]() :
:
![]() ,
значения многочлена
и его производной
при
,
значения многочлена
и его производной
при
![]() :
:
![]() ,
,
![]() ,
откуда
,
откуда
![]() ,
,
![]() .
.
7. Разложение дробей на простейшие.
Определение 1.
Дробно-рациональной
функцией называется
отношение (частное) пары многочленов
и
,
где
![]() .
Краткая запись
.
Краткая запись
![]() .
.
Одна и та же дробь
может быть представлена в виде частного
различных пар многочленов. Если НОД![]() =1,
то
– несократимая запись. Такая запись
существует у каждой дроби и она
единственна, если многочлен
нормирован.
=1,
то
– несократимая запись. Такая запись
существует у каждой дроби и она
единственна, если многочлен
нормирован.
Определение 2. Дробь называется правильной, если степень ее числителя меньше степени знаменателя.
Определение 3.
Комплексная
простейшая дробь
– это дробь с несократимой записью
![]() ,
где
,
где
![]() ,
а
,
а
![]() .
.
Определение 4.
Вещественная
простейшая дробь
– это дробь с несократимой записью
одного из двух типов:
,
![]() ,
где
,
где
![]() ,
,
![]() ,
.
,
.
Теорема 1. Всякая правильная дробь представима в виде суммы простейших комплексных дробей; всякая правильная вещественная дробь представима в виде суммы простейших вещественных дробей.
Один из способов
разложения дроби на простейшие дает
формула Лагранжа. Эта формула применима
к дробям
![]() ,
если
,
если
![]() не имеет кратных корней и при разложении
на вещественные простейшие имеет только
вещественные корни. Если
не имеет кратных корней и при разложении
на вещественные простейшие имеет только
вещественные корни. Если
![]() ,
,
![]() при
при
![]() ,
то
,
то
![]() .
Значение производной
.
Значение производной
![]() можно вычислять по формуле
можно вычислять по формуле
![]() .
.
Для дроби
![]() формула Лагранжа не применима. В этом
случае можно получить требуемое, разложив
многочлен
по степеням многочлена
.
формула Лагранжа не применима. В этом
случае можно получить требуемое, разложив
многочлен
по степеням многочлена
.
ПРИМЕРЫ:
1. Разложить
![]() на простейшие комплексные дроби.
на простейшие комплексные дроби.
Решение:
Заметим, что знаменатель
![]() не имеет кратных корней, его корни
,
,
не имеет кратных корней, его корни
,
,
![]() ,
,
![]() – корни четвертой степени из
;
– корни четвертой степени из
;
![]() .
По формуле Лагранжа:
.
По формуле Лагранжа:
 2.
Разложить
2.
Разложить
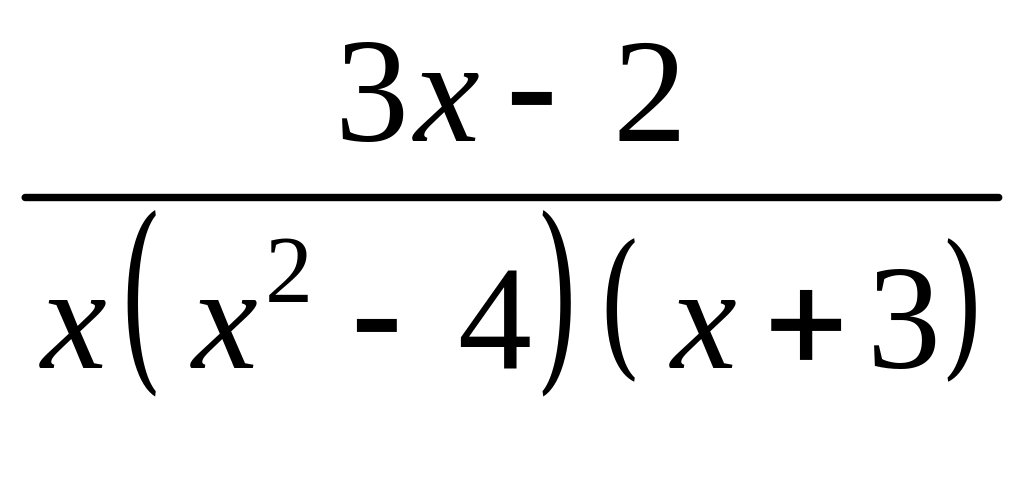 на вещественные простейшие дроби.
на вещественные простейшие дроби.
Решение: У
знаменателя
![]() все корни просты и вещественны,
следовательно, можно применить формулу
Лагранжа:
все корни просты и вещественны,
следовательно, можно применить формулу
Лагранжа:

3. Разложить
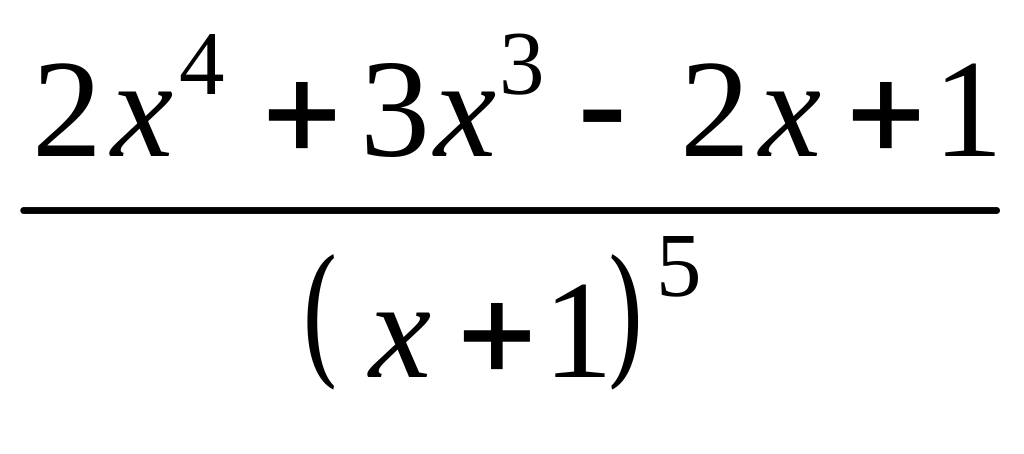 на простейшие вещественные дроби.
на простейшие вещественные дроби.
Решение: Для решения задачи используем схему Горнера:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 4.
Разложить
4.
Разложить
 на простейшие вещественные дроби.
на простейшие вещественные дроби.
Решение:
Заметим, что дискриминант
![]() отрицателен. Введем обозначения:
отрицателен. Введем обозначения:
![]() ;
;
![]() .
Разделим многочлен
на многочлен
с остатком:
.
Разделим многочлен
на многочлен
с остатком:
![]() ,
т.е.
,
т.е.
![]() ,
где
,
где
![]() ,
,
![]() .
Теперь разделим
.
Теперь разделим
![]() на
:
на
:
![]() ,
т.е.
,
т.е.
![]() ,
где
,
где
![]() ,
,
![]() .
Таким образом,
.
Таким образом,
![]() .
.
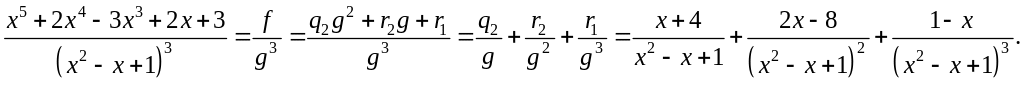 5.
Разложить
5.
Разложить
![]() на простейшие комплексные дроби.
на простейшие комплексные дроби.
Решение: Воспользуемся видом разложения дроби на простейшие:
![]() .
.
Для нахождения
коэффициентов
и
домножим это равенство на
:
![]() .
При
.
При
![]() получаем
получаем
![]() .
Теперь продифференцируем полученное
уравнение:
.
Теперь продифференцируем полученное
уравнение:
![]() .
При
получаем
.
При
получаем
![]() .
.
Теперь так же
находим коэффициенты
![]() ,
,
![]() ,
,
![]() .
Домножаем сначала на
:
.
Домножаем сначала на
:
![]() .
При
.
При
![]() :
:
![]() .
После дифференцирования:
.
После дифференцирования:
![]() ,
при
:
,
при
:
![]() .
Еще раз дифференцируем:
.
Еще раз дифференцируем:
![]() ,
:
,
:
![]() .
.
Итак,
![]() .
.
6. Разложить
 на простейшие вещественные дроби.
на простейшие вещественные дроби.
Решение: Заметим, что в разложении будет единственное слагаемое со знаменателем, имеющим корень . Найдем сначала его:
 ,
домножаем на
:
,
домножаем на
:
 и при
получаем
и при
получаем
![]() .
.
Теперь находим разность
 .
Разложим числитель по степеням
.
Разложим числитель по степеням
![]() :
:
![]() .
Тогда
.
Тогда
 .
.
