
- •1. Алгебраические структуры.
- •2. Определение многочлена. Операции над многочленами.
- •3. Кольцо многочленов над областью целостности.
- •4. Деление многочленов с остатком. Разложение многочлена на множители.
- •5. Наибольший общий делитель. Алгоритм евклида.
- •6. Кратность корня и производная многочлена.
- •7. Разложение дробей на простейшие.
- •Задания к типовому расчету
- •Библиографический список
- •Содержание
- •190031, СПб, Московский пр., 9.
3. Кольцо многочленов над областью целостности.
Далее будем рассматривать только многочлены с коэффициентами из области целостности K (кольцо без делителей нуля называют областью целостности), т.е. из кольца K, в котором произведение двух элементов может равняться нулю, если только один из сомножителей равен нулю. Это всегда будет подразумеваться, даже если не будет оговорено специально.
При произведении
многочленов
степени n
и
![]() степени m
старший член равен
степени m
старший член равен
![]() (это коэффициент при
(это коэффициент при
![]() ).
Так как в кольце нет делителей нуля, то
).
Так как в кольце нет делителей нуля, то
![]() и, значит,
и, значит,
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Итак, произведение двух ненулевых многочленов – ненулевой многочлен, поэтому справедлива следующая теорема:
Теорема 1. Кольцо многочленов над областью целостности само является областью целостности.
Данное нами алгебраическое определение многочлена не содержит никакого упоминания о функциях. Тем не менее, с каждым многочленом над областью целостности K можно естественным образом связать функцию, которая определена на K и принимает значения в K.
Пусть
– многочлен с коэффициентами из K.
Для любого
![]() положим
положим
![]() ,
,
где выражение в
правой части понимается как результат
операций в кольце K.
Получаемый при этом элемент
![]() называется значением многочлена f(x)
в точке x0.
Таким образом, каждому элементу x0
кольца K
сопоставляется элемент f(x0)
того же кольца и тем самым определяется
функция на K
со значениями в K.
называется значением многочлена f(x)
в точке x0.
Таким образом, каждому элементу x0
кольца K
сопоставляется элемент f(x0)
того же кольца и тем самым определяется
функция на K
со значениями в K.
Вообще говоря, соответствие между многочленами и определяемыми ими функциями не является взаимно однозначным. Однако, если кольцо K бесконечно, то различным многочленам из кольца K[x] всегда соответствуют различные функции.
4. Деление многочленов с остатком. Разложение многочлена на множители.
Здесь и далее,
многочлен
![]() от
аргумента
от
аргумента
![]() будем обозначать через
будем обозначать через
![]() .
.
Определение 1.
Число
![]() называют корнем
многочлена
если
называют корнем
многочлена
если
![]() .
.
Замечание: Если
– многочлен с вещественными коэффициентами
и
его корень, то сопряженное число
![]() также есть корень многочлена
.
также есть корень многочлена
.
Определение 2.
Говорят, что многочлен
делится
на многочлен
![]() (
(![]() )
если существует такой многочлен
)
если существует такой многочлен
![]() ,
что
,
что
![]() .
.
Всякий многочлен
имеет делители вида
![]() и
и
![]() ,
где
,
где
![]() .
Такие делители называются тривиальными.
.
Такие делители называются тривиальными.
Определение 3. Многочлен называется неприводимым, если он не имеет нетривиальных делителей.
Простейшие свойства делимости многочленов:
Если
 и
и
 ,
то
,
то
 .
.Если , то для любого многочлена
 .
.Нуль делится на любой многочлен.
Если и
 ,
то
,
то
 ,
где
,
где
 – некоторое число, отличное от нуля.
– некоторое число, отличное от нуля.Если ,
 ,
то
,
то
 .
.
Теорема
1 (Теорема
Безу). Остаток от деления многочлена
на линейный двучлен
![]() равен
равен
![]() .
.
Теорема 2 (Теорема Декарта). Многочлен делится на двучлен тогда и только тогда есть корень многочлена .
Деление с остатком многочлена на двучлен можно выполнять при помощи схемы Горнера. Для этого составляется таблица
|
|
|
|
|
|
|
|
|
|
|
|
В первой строке здесь стоят коэффициенты многочлена , во второй строке первый элемент равен , каждый последующий элемент получается из предыдущего умножением его на и прибавлением числа, стоящего над ним. Получаем
![]() .
.
Теорема 3. Всякий многочлен можно разложить на линейные множители с комплексными коэффициентами, т.е. представить в виде
![]() (может быть
(может быть
![]() ).
).
При этом
![]() – старший коэффициент многочлена
;
– старший коэффициент многочлена
;
![]() – его корни (не обязательно различные),
и любой корень многочлена
совпадает с одним из чисел
– его корни (не обязательно различные),
и любой корень многочлена
совпадает с одним из чисел
![]() .
Такое разложение единственно с точностью
до порядка сомножителей. Если в этом
разложении объединить одинаковые
множители в степени, то
.
Такое разложение единственно с точностью
до порядка сомножителей. Если в этом
разложении объединить одинаковые
множители в степени, то
![]() ,
,
где
![]() – все различные корни многочлена
.
– все различные корни многочлена
.
Теорема 4. Всякий многочлен с вещественными коэффициентами можно разложить на вещественные множители 1-й и 2-й степени:
![]()
(может быть
![]() или
или
![]() ),
где
),
где
![]() для
для
![]() .
При этом:
.
При этом:
– старший коэффициент многочлена ;
 – все его
вещественные корни;
– все его
вещественные корни;каждый из многочленов
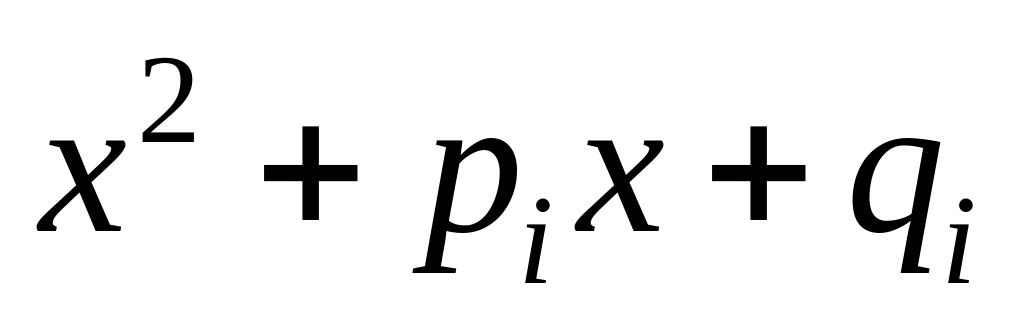 неразложим на вещественные множители
меньшей (т.е 1-й) степени и имеет два
невещественных сопряженных (тем самым
различных) корня, являющихся в то же
время корнями многочлена
;
такими корнями исчерпываются все
невещественные корни многочлена
.
неразложим на вещественные множители
меньшей (т.е 1-й) степени и имеет два
невещественных сопряженных (тем самым
различных) корня, являющихся в то же
время корнями многочлена
;
такими корнями исчерпываются все
невещественные корни многочлена
.
ПРИМЕРЫ:
1. Разложить
многочлен
по степеням
![]() ,
где
,
где
![]() ,
,
![]() .
.
Решение: Для
решения задачи применим схему Горнера.
Заметим, что если многочлен
разложен по степеням
,
т.е.
![]() ,
то
– остаток при делении многочлена
на
,
– остаток при делении предыдущего
частного на
и т.д.
,
то
– остаток при делении многочлена
на
,
– остаток при делении предыдущего
частного на
и т.д.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Получили, что
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
т.е.
,
т.е.
![]()
2. Разложить
по степеням
многочлен
![]() ,
где
,
где
![]() .
.
Решение: Для
решения задачи можно в многочлене
заменить
на
![]() ,
но эта процедура будет очень громоздка.
Поэтому здесь удобно применить схему
Горнера. Разложим многочлен
по степеням
,
но эта процедура будет очень громоздка.
Поэтому здесь удобно применить схему
Горнера. Разложим многочлен
по степеням
![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]() Если в полученном
разложении заменить
на
,
то получится искомое разложение
Если в полученном
разложении заменить
на
,
то получится искомое разложение
![]()
