Государственное образовательное учреждение

высшего профессионального образования

“ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ МИНИСТЕРСТВА ПУТЕЙ СООБЩЕНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ”

ТЕОРИЯ МНОГОЧЛЕНОВ

Методическое пособие

САНКТ-ПЕТЕРБУРГ

2007

УДК 512.5

ББК В14

Литвинова В.В.

Теория многочленов: Учебное пособие. – СПб.: Петербургский государственный университет путей сообщения, 2007. – 26 с.

Библиогр.: 3 наз.

Содержит краткое изложение теории многочленов. Предполагается, что читатель знаком с курсом линейной алгебры и основными понятиями теории групп. Рассматривается большое количество примеров и приводятся варианты индивидуальных заданий.

Предназначено для студентов инженерных специальностей, а также для студентов технических университетов специальности Прикладная математика.

УДК 512.5

Рецензент д-р ф.-м. наук, проф. А.Г.Басуев (Санкт-Петербургский университет технологии и дизайна)

© В.В. Литвинова, 2007

© Петербургский государст­венный универ­ситет путей сообщения, 2007

Во всем многообразии функций многочлены занимают, на первый взгляд, очень скромное место. Однако это первое впечатление обманчиво. Хотя выражения типа , , намного лаконичнее, с вычислительной точки зрения они бессодержательны: для вычисления, скажем чисел , или нужны специальные приближённые формулы (или таблицы, составленные с помощью тех же формул). Как правило, в таких формулах появляются многочлены.

В пособии понятие многочлена расширяется по сравнению с понятием многочлена из школьной алгебры. Чтобы ввести новое определение многочлена понадобятся определения основных алгебраических структур.

1. Алгебраические структуры.

Определение 1. Операцией на множестве называется функция , которая сопоставляет паре элементов множества элемент того же множества, т.е. .

Обозначение для произвольной операции: .

Таким образом, сложение (+) и умножение ( ) являются операциями.

Определение 2. Множество называется группой, если на нем задана операция со следующими свойствами:

1. – ассоциативность;

2. – наличие единичного элемента;

3. – наличие обратного элемента.

Определение 3. Группа называется коммутативной или абелевой, если операция в ней коммутативна, т.е. .

В качестве примера можно рассмотреть множество целых чисел . Относительно операции сложения множество будет являться группой (единичным элементом будет , а обратным – элемент с обратным знаком), кроме того, эта группа будет абелевой. С другой стороны, множество относительно операции умножения не будет группой (не все элементы имеют обратный).

Определение 4. Множество называется кольцом, если в нем определены две операции: сложения и умножения. Относительно операции сложения множество является абелевой группой, а относительно умножения множество является полугруппой. Умножение и сложение связаны между собой законом дистрибутивности:

1. ;

2. .

Определение 5. Кольцо называется коммутативным, если операция умножения коммутативна. Если полугруппа относительно умножения имеет единицу, то кольцо называется кольцом с единицей.

Примерами колец могут служить множества рациональных и комплексных чисел . Причем оба эти кольца будут коммутативными и иметь единицу (т.к. операция умножения коммутативна, а единицей будет служить ).

Также кольцом будет являться множество неособых матриц одинакового порядка (определитель которых отличен от нуля). В качестве единицы относительно сложения будет нулевая матрица, а единицей относительно умножения будет являться единичная матрица. Но оно не будет коммутативным, поскольку операция умножения матриц коммутативностью не обладает.

2. Определение многочлена. Операции над многочленами.

Определение 1. Пусть K – некоторое коммутативное кольцо с единицей, и пусть x – буква, посторонняя для кольца K. Одночленом степени m от буквы x с коэффициентом из K называется выражение , где , m – целое неотрицательное число.

Будем считать, что . Таким образом, элементы кольца K являются одночленами частного вида.

Определение 2. Формальное выражение, состоящее из нескольких одночленов, соединенных знаком +, называется многочленом или полиномом от x с коэффициентами из K.

Предполагается, что порядок следования одночленов безразличен, подобные одночлены можно соединять, а также вставлять и выбрасывать одночлены с нулевыми коэффициентами. Без нарушения общности можно считать полином записанным в канонической форме (т.е. в порядке убывания степеней) или в порядке возрастания степеней .

Определение 3. Два полинома считаются равными, если они составлены в канонической записи из одинаковых одночленов, т.е. в том и только в том случае, если .

Определение 4. Суммой двух полиномов называется полином, получающийся посредством объединения одночленов, составляющих слагаемые. Разумеется, после объединения следует привести подобные члены. Таким образом, , где .

Замечание: Если многочлены f(x) и g(x) имеют разное число одночленов, то, подписав необходимое число одночленов с нулевыми коэффициентами к одному из них, в котором число одночленов меньше, можно добиться их равенства в обоих многочленах. Поэтому складывать можно многочлены с разным числом одночленов.

Заметим, что операция сложения многочленов обладает такими же свойствами, что и операция сложения элементов кольца K, т.е. ассоциативна, коммутативна; полином, все коэффициенты которого нули, является нейтральным элементом сложения полиномов; для каждого полинома существует ему противоположный, противоположный к полиному является полином . Итак, множество полиномов с операцией сложения образует коммутативную группу.

Определение 4. Произведением двух полиномов называется полином, составленный из произведений всех членов первого сомножителя на все члены второго.

Таким образом, , где .

Умножение многочленов ассоциативно, коммутативно и дистрибутивно относительно сложения, роль единицы при умножении многочленов играет многочлен (где 1 – единица кольца K). Таким образом, множество полиномов от буквы x с коэффициентами из кольца составляет кольцо по отношению к выше определенным операциям сложения и умножения полиномов. Кольцо это коммутативно оно называется кольцом полиномов от буквы x над кольцом K и обозначается K[x].

Пусть , причем . Одночлен называется высшим (старшим) членом полинома f(x) и показатель n называется степенью f(x) и обозначается deg f. Нулевой полином не имеет высшего члена в смысле данного определения и считается, что он равен нулю. Коэффициент называется свободным членом. Многочлен, старший коэффициент которого равен единице, называется нормированным.

Простейшие свойства степени многочлена:

1. ;

2. .

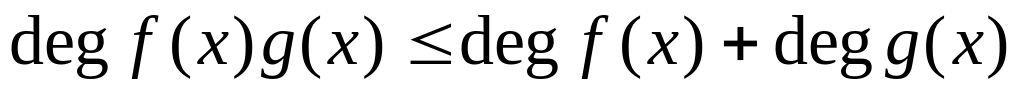ПРИМЕРЫ:

1. Найти , где .

Решение: Согласно определению суммы многочленов получаем:

.

2. Найти , где .

Решение: По определению произведения многочленов имеем:

.