Построение эмпирической функции.
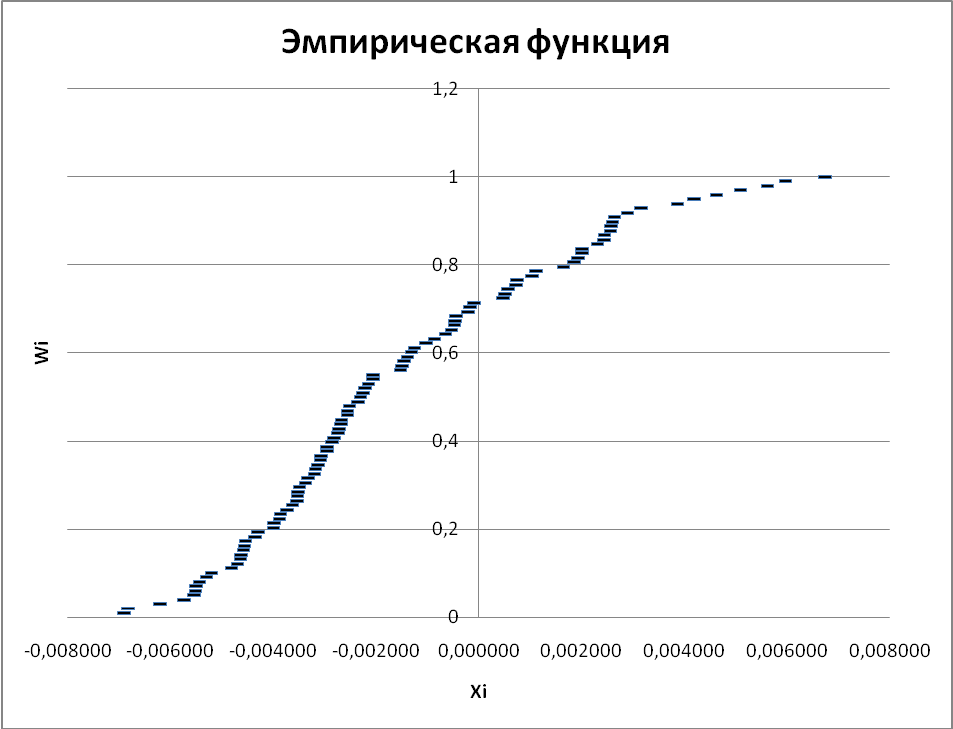
Сгруппированный статистический ряд.
Интервал
|
|
(-0,00463;-0,00235) |
(-0,00235; -7,7E-05) |
(-7,7Е-05;0,00219) |
(0,00219; 0,00447) |
(0,00447; 0,00675) |
|
кол-во |
14 |
34 |
27 |
7 |
11 |
5 |
|
отн.част |
0,142857
|
0,346939
|
0,27551
|
0,071429
|
0,112245
|
0,05102
|
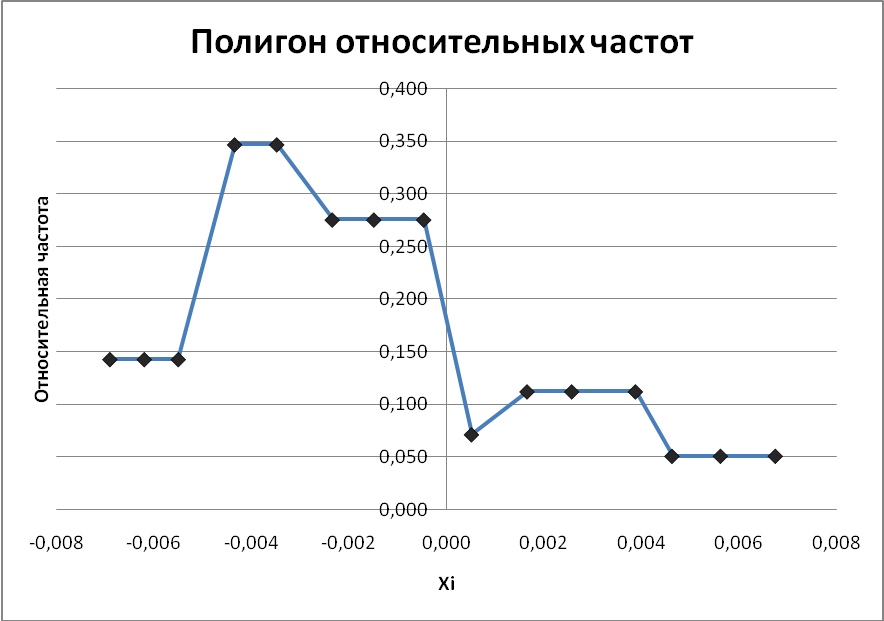
Подбор соответствующего теоретического распределения.
Проверка на вероятность соответствия по - критерию.
По виду гистограммы
можно предположить, что наблюдаемая
случайная величина имеет нормальное
распределение -
.
Функция плотности вероятности нормального
распределения имеет вид
,
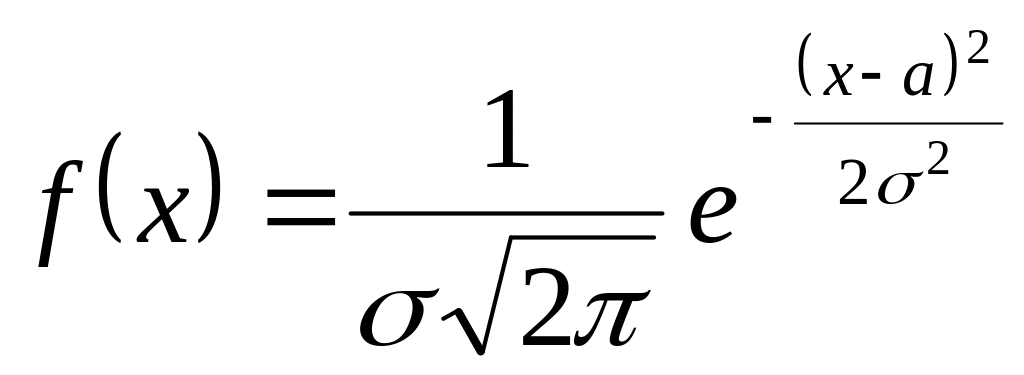где параметры
и
неизвестны.
В качестве значений параметров распределения возьмем их оценки, полученные на основе опытных данных. Оценкой параметра является величина
,
оценкой параметра
является величина
В обеих формулах
- середина
-го
интервала.
;
s
= 4,05.
Зададимся уровнем
значимости, например,
.
Для получения надежных выводов на основе
критерия хи-квадрат нужно объединить
первый интервал, содержащий мало
наблюдений, со вторым интервалом. Тогда
имеем всего
интервалов. Определим
,
(
– число степеней свободы,
– число неизвестных параметров). Итак,
.
Вычислим
.
Для этого сначала вычислим вероятности,
попадания исследуемой случайной величины
в каждый интервал, согласно гипотезе.
В случае нормального распределения они
вычисляются по формуле:
.
где
– функция Лапласа.
.
ni |
pi |
npi |
ni–npi |
(ni–npi)2 |
(ni–npi)2 |
npi |
|||||
21 |
0,2336 |
22,893 |
-1,8928 |
3,58269184 |
0,15649863 |
37 |
0,2837 |
27,803 |
9,1974 |
84,5921668 |
3,04259914 |
17 |
0,2648 |
25,95 |
-8,9504 |
80,1096602 |
3,08702988 |
17 |
0,1463 |
14,337 |
2,6626 |
7,08943876 |
0,49447171 |
6 |
0,0468 |
4,5864 |
1,4136 |
1,99826496 |
0,43569356 |
Величина
равна сумме значений в последнем столбце
таблицы.
Сравним
и
:
.
Таким образом, при выбранном уровне
значимости
принадлежит
критической области
,
а значит: гипотеза опытным данным
противоречит. Следует отметить, что
вероятность того, что мы ошибаемся,
меньше 0,05.
«Мода случайной величины» – одна из числовых характеристик распределения вероятностей случайной величины; для случайной величины, имеющей плотность вероятностей f(x) определяется как любая точка максимума f(x).
Modξ = 0,012
«Медиана» – одна из числовых характеристик распределения вероятностей случайной величины; для случайной величины, имеющей строго монотонную функцию распределения F(x) определяется как единственный корень уравнения F(x) = 1 / 2; в общем случае определяется неоднозначно, а иногда не существует.
В симметричном случае — совпадает с модой или математическим ожиданием, если последнее существует; употребляется реже, чем математическое ожидание и чаще, чем мода.
Medξ = 0,012
«Эксцесс» – мера остроты пика распределения случайной величины.
Пусть
задана случайная величина X,
такая что
.
Пусть μ4
обозначает четвёртый центральный
момент:
,
а
—
стандартное отклонение X.
Тогда коэффициент эксцесса задаётся
формулой:
.
«Коэффицет асимметрии» – величина, характеризующая асимметрию распределения данной случайной величины.
Пусть
задана случайная величина X,
такая что
.
Пусть μ3
обозначает третий центральный момент:
,
а
—
стандартное отклонение X.
Тогда коэффициент асимметрии задаётся
формулой:
.
Регрессионный анализ.
Основан на использовании полиномиальной модели.
Цель: определение наличия характера связи между переменными.
а) Линейный регрессионный анализ.
n=10 |
n=20 |
n=30 |
n=40 |
n=50 |
0,01100 |
0,01068 |
|
0,009 |
0,009 |
0,01100 |
0,01076 |
0,01093 |
0,009 |
0,009 |
0,01100 |
0,01084 |
0,01096 |
0,009 |
0,009 |
0,01100 |
0,01092 |
0,01099 |
0,009 |
0,009 |
0,01100 |
0,011 |
0,01102 |
0,009 |
0,009 |
0,01100 |
0,01108 |
0,01105 |
0,009 |
0,009 |
0,01100 |
0,01116 |
0,01108 |
0,009 |
0,009 |
0,01100 |
0,01124 |
0,01111 |
0,009 |
0,009 |
0,01100 |
0,01132 |
0,01114 |
0,009 |
0,009 |
0,01100 |
0,0114 |
0,01117 |
0,009 |
0,009 |
0,01100 |
0,01148 |
0,0112 |
0,009 |
0,009 |
0,01100 |
0,01156 |
0,01123 |
0,009 |
0,009 |
0,01100 |
0,01164 |
0,01126 |
0,009 |
0,009 |
0,01100 |
0,01172 |
0,01129 |
0,009 |
0,009 |
0,01100 |
0,0118 |
0,01132 |
0,009 |
0,009 |
0,01100 |
0,01188 |
0,01135 |
0,009 |
0,009 |
0,01100 |
0,01196 |
0,01138 |
0,009 |
0,009 |
0,01100 |
0,01204 |
0,01141 |
0,009 |
0,009 |
0,01100 |
0,01212 |
0,01144 |
0,009 |
0,009 |
0,01100 |
0,0122 |
0,01147 |
0,009 |
0,009 |
0,01100 |
0,01228 |
0,0115 |
0,009 |
0,009 |
0,01100 |
0,01236 |
0,01153 |
0,009 |
0,009 |
0,01100 |
0,01244 |
0,01156 |
0,009 |
0,009 |
0,01100 |
0,01252 |
0,01159 |
0,009 |
0,009 |
0,01100 |
0,0126 |
0,01162 |
0,009 |
0,009 |
0,01100 |
0,01268 |
0,01165 |
0,009 |
0,009 |
0,01100 |
0,01276 |
0,01168 |
0,009 |
0,009 |
0,01100 |
0,01284 |
0,01171 |
0,009 |
0,009 |
0,01100 |
0,01292 |
0,01174 |
0,009 |
0,009 |
0,01100 |
0,013 |
0,01177 |
0,009 |
0,009 |
0,01100 |
0,01308 |
0,0118 |
0,009 |
0,009 |
0,01100 |
0,01316 |
0,01183 |
0,009 |
0,009 |
0,01100 |
0,01324 |
0,01186 |
0,009 |
0,009 |
0,01100 |
0,01332 |
0,01189 |
0,009 |
0,009 |
0,01100 |
0,0134 |
0,01192 |
0,009 |
0,009 |
0,01100 |
0,01348 |
0,01195 |
0,009 |
0,009 |
0,01100 |
0,01356 |
0,01198 |
0,009 |
0,009 |
0,01100 |
0,01364 |
0,01201 |
0,009 |
0,009 |
0,01100 |
0,01372 |
0,01204 |
0,009 |
0,009 |
0,01100 |
0,0138 |
0,01207 |
0,009 |
0,009 |
0,01100 |
0,01388 |
0,0121 |
0,009 |
0,009 |
0,01100 |
0,01396 |
0,01213 |
0,009 |
0,009 |
0,01100 |
0,01404 |
0,01216 |
0,009 |
0,009 |
0,01100 |
0,01412 |
0,01219 |
0,009 |
0,009 |
0,01100 |
0,0142 |
0,01222 |
0,009 |
0,009 |
0,01100 |
0,01428 |
0,01225 |
0,009 |
0,009 |
0,01100 |
0,01436 |
0,01228 |
0,009 |
0,009 |
0,01100 |
0,01444 |
0,01231 |
0,009 |
0,009 |
0,01100 |
0,01452 |
0,01234 |
0,009 |
0,009 |
0,01100 |
0,0146 |
0,01237 |
0,009 |
0,009 |
0,01100 |
0,01468 |
0,0124 |
0,009 |
|
0,01100 |
0,01476 |
0,01243 |
0,009 |
|
0,01100 |
0,01484 |
0,01246 |
0,009 |
|
0,01100 |
0,01492 |
0,01249 |
0,009 |
|
0,01100 |
0,015 |
0,01252 |
0,009 |
|
0,01100 |
0,01508 |
0,01255 |
0,009 |
|
0,01100 |
0,01516 |
0,01258 |
0,009 |
|
0,01100 |
0,01524 |
0,01261 |
0,009 |
|
0,01100 |
0,01532 |
0,01264 |
0,009 |
|
0,01100 |
0,0154 |
0,01267 |
0,009 |
|
0,01100 |
0,01548 |
0,0127 |
|
|
0,01100 |
0,01556 |
0,01273 |
|
|
0,01100 |
0,01564 |
0,01276 |
|
|
0,01100 |
0,01572 |
0,01279 |
|
|
0,01100 |
0,0158 |
0,01282 |
|
|
0,01100 |
0,01588 |
0,01285 |
|
|
0,01100 |
0,01596 |
0,01288 |
|
|
0,01100 |
0,01604 |
0,01291 |
|
|
0,01100 |
0,01612 |
0,01294 |
|
|
0,01100 |
0,0162 |
0,01297 |
|
|
0,01100 |
0,01628 |
0,013 |
|
|
0,01100 |
0,01636 |
|
|
|
0,01100 |
0,01644 |
|
|
|
0,01100 |
0,01652 |
|
|
|
0,01100 |
0,0166 |
|
|
|
0,01100 |
0,01668 |
|
|
|
0,01100 |
0,01676 |
|
|
|
0,01100 |
0,01684 |
|
|
|
0,01100 |
0,01692 |
|
|
|
0,01100 |
0,017 |
|
|
|
0,01100 |
|
|
|
|
0,01100 |
|
|
|
|
0,01100 |
|
|
|
|
0,01100 |
|
|
|
|
0,01100 |
|
|
|
|
0,01100 |
|
|
|
|
0,01100 |
|
|
|
|
0,01100 |
|
|
|
|
|
|
|
|
|
График.
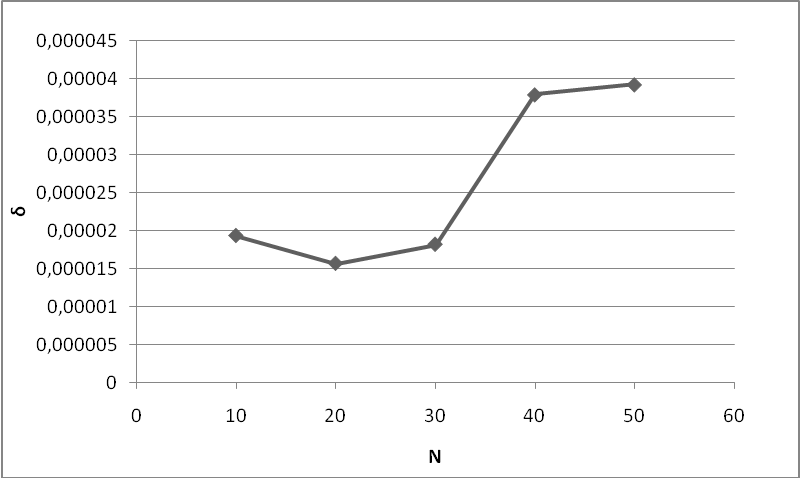
Минимальное значение при σ20.
б) Квадратичный регрессионный анализ.
n=10 |
n=20 |
n=30 |
n=40 |
n=50 |
0,01289 |
0,02423 |
0,0072 |
0,0138 |
0,009008 |
0,01396 |
0,02552 |
0,007078 |
0,014002 |
0,009008 |
0,01521 |
0,02687 |
0,006952 |
0,014208 |
0,009008 |
0,01664 |
0,02828 |
0,006822 |
0,014418 |
0,009008 |
0,01825 |
0,02975 |
0,006688 |
0,014632 |
0,009009 |
0,02004 |
0,03128 |
0,00655 |
0,01485 |
0,009009 |
0,02201 |
0,03287 |
0,006408 |
0,015072 |
0,009009 |
0,02416 |
0,03452 |
0,006262 |
0,015298 |
0,00901 |
0,02649 |
0,03623 |
0,006112 |
0,015528 |
0,00901 |
0,029 |
0,038 |
0,005958 |
0,015762 |
0,00901 |
0,03169 |
0,03983 |
0,0058 |
0,016 |
0,009011 |
0,03456 |
0,04172 |
0,005638 |
0,016242 |
0,009011 |
0,03761 |
0,04367 |
0,005472 |
0,016488 |
0,009012 |
0,04084 |
0,04568 |
0,005302 |
0,016738 |
0,009012 |
0,04425 |
0,04775 |
0,005128 |
0,016992 |
0,009012 |
0,04784 |
0,04988 |
0,00495 |
0,01725 |
0,009013 |
0,05161 |
0,05207 |
0,004768 |
0,017512 |
0,009013 |
0,05556 |
0,05432 |
0,004582 |
0,017778 |
0,009013 |
0,05969 |
0,05663 |
0,004392 |
0,018048 |
0,009014 |
0,064 |
0,059 |
0,004198 |
0,018322 |
0,009014 |
0,06849 |
0,06143 |
0,004 |
0,0186 |
0,009015 |
0,07316 |
0,06392 |
0,003798 |
0,018882 |
0,009015 |
0,07801 |
0,06647 |
0,003592 |
0,019168 |
0,009016 |
0,08304 |
0,06908 |
0,003382 |
0,019458 |
0,009016 |
0,08825 |
0,07175 |
0,003168 |
0,019752 |
0,009016 |
0,09364 |
0,07448 |
0,00295 |
0,02005 |
0,009017 |
0,09921 |
0,07727 |
0,002728 |
0,020352 |
0,009017 |
0,10496 |
0,08012 |
0,002502 |
0,020658 |
0,009018 |
0,11089 |
0,08303 |
0,002272 |
0,020968 |
0,009018 |
0,117 |
0,086 |
0,002038 |
0,021282 |
0,009019 |
0,12329 |
0,08903 |
0,0018 |
0,0216 |
0,009019 |
0,12976 |
0,09212 |
0,001558 |
0,021922 |
0,00902 |
0,13641 |
0,09527 |
0,001312 |
0,022248 |
0,00902 |
0,14324 |
0,09848 |
0,001062 |
0,022578 |
0,009021 |
0,15025 |
0,10175 |
0,000808 |
0,022912 |
0,009021 |
0,15744 |
0,10508 |
0,00055 |
0,02325 |
0,009022 |
0,16481 |
0,10847 |
0,000288 |
0,023592 |
0,009022 |
0,17236 |
0,11192 |
2,2E-05 |
0,023938 |
0,009023 |
0,18009 |
0,11543 |
-0,00025 |
0,024288 |
0,009023 |
0,188 |
0,119 |
-0,00052 |
0,024642 |
0,009024 |
0,19609 |
0,12263 |
-0,0008 |
0,025 |
0,009024 |
0,20436 |
0,12632 |
-0,00108 |
0,025362 |
0,009025 |
0,21281 |
0,13007 |
-0,00137 |
0,025728 |
0,009025 |
0,22144 |
0,13388 |
-0,00166 |
0,026098 |
0,009026 |
0,23025 |
0,13775 |
-0,00195 |
0,026472 |
0,009027 |
0,23924 |
0,14168 |
-0,00225 |
0,02685 |
0,009027 |
0,24841 |
0,14567 |
-0,00255 |
0,027232 |
0,009028 |
0,25776 |
0,14972 |
-0,00286 |
0,027618 |
0,009028 |
0,26729 |
0,15383 |
-0,00317 |
0,028008 |
0,009029 |
0,277 |
0,158 |
-0,00348 |
0,028402 |
0,009029 |
0,28689 |
0,16223 |
-0,0038 |
0,0288 |
0,00903 |
0,29696 |
0,16652 |
-0,00412 |
0,029202 |
|
0,30721 |
0,17087 |
-0,00445 |
0,029608 |
|
0,31764 |
0,17528 |
-0,00478 |
0,030018 |
|
0,32825 |
0,17975 |
-0,00511 |
0,030432 |
|
0,33904 |
0,18428 |
-0,00545 |
0,03085 |
|
0,35001 |
0,18887 |
-0,00579 |
0,031272 |
|
0,36116 |
0,19352 |
-0,00614 |
0,031698 |
|
0,37249 |
0,19823 |
-0,00649 |
0,032128 |
|
0,384 |
0,203 |
-0,00684 |
0,032562 |
|
0,39569 |
0,20783 |
-0,0072 |
0,033 |
|
0,40756 |
0,21272 |
-0,00756 |
|
|
0,41961 |
0,21767 |
-0,00793 |
|
|
0,43184 |
0,22268 |
-0,0083 |
|
|
0,44425 |
0,22775 |
-0,00867 |
|
|
0,45684 |
0,23288 |
-0,00905 |
|
|
0,46961 |
0,23807 |
-0,00943 |
|
|
0,48256 |
0,24332 |
-0,00982 |
|
|
0,49569 |
0,24863 |
-0,01021 |
|
|
0,509 |
0,254 |
-0,0106 |
|
|
0,52249 |
0,25943 |
-0,011 |
|
|
0,53616 |
0,26492 |
|
|
|
0,55001 |
0,27047 |
|
|
|
0,56404 |
0,27608 |
|
|
|
0,57825 |
0,28175 |
|
|
|
0,59264 |
0,28748 |
|
|
|
0,60721 |
0,29327 |
|
|
|
0,62196 |
0,29912 |
|
|
|
0,63689 |
0,30503 |
|
|
|
0,652 |
0,311 |
|
|
|
0,66729 |
|
|
|
|
0,68276 |
|
|
|
|
0,69841 |
|
|
|
|
0,71424 |
|
|
|
|
0,73025 |
|
|
|
|
0,74644 |
|
|
|
|
0,76281 |
|
|
|
|
0,77936 0.79609 0.813 |
|
|
|
|
График.
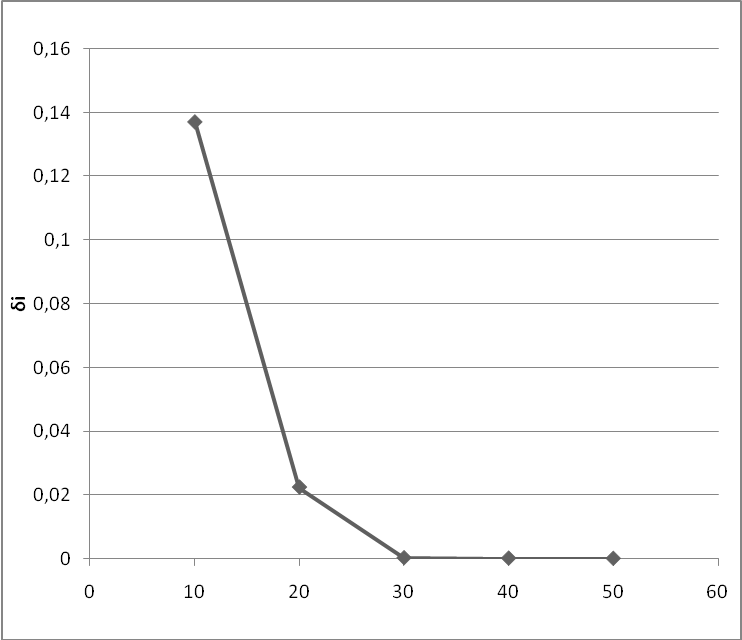
Минимальное значение при σ50.
Заключение.
Исследуя данную работу, я закрепила знания основных характеристик теории вероятностей и математической статистики, таких как: математическое ожидание случайной величины, дисперсия, среднеквадратическое отклонение и другие. Научилась строить эмпирические функции, полигоны и гистограммы относительных частот, разобралась как проверять вероятность соответствия по -критерию, а так же проводить регрессионный анализ.