Практическая работа № 2. Тема: Задача управления запасами с учетом убытков из-за неудовлетворенного спроса и задача управления запасами при случайном спросе

Цель работы: Научиться решать задачи определения оптимальной поставки запасов на предприятие.

2.1. Краткие сведения из теории

Постановка задачи. Пусть на предприятии вследствие не­удовлетворенного спроса возникают убытки, характеризующиеся величиной С_у на единицу ресурса в единицу времени. В течение времени t_i каждого периода t уровень запаса достаточен для удовлетворения спроса, а затем в течение интервала t₂ запас отсутствует, причем неудовлетворенный спрос покрывается из следующей партии с момента поступления на склад. Пусть потребность в материале составляет Q единиц в период Т.

Определить, какими должны быть поставляемая S и потребная V партии, чтобы затраты на доставку и хранение с учетом неудовлетворенного спроса были минимальными.

Выявление основных особенностей, взаимосвязей и количест­венных закономерностей. Обозначения как и в предыдущей работе. Гра­фически движение запасов при неполном удовлетворении спроса представлено на рис. 2.1.

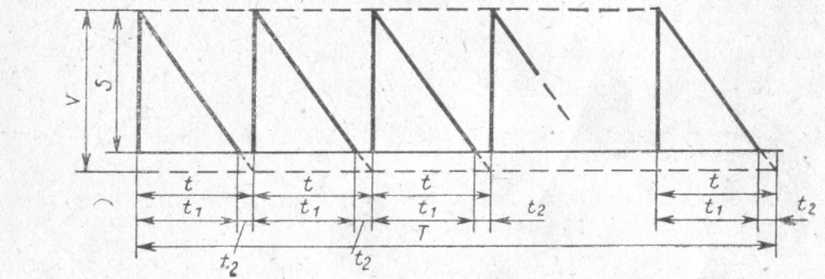
Рис. 2.1.Движение запасов с учетом убытков из-за неудовлетворенного спроса

По графику легко составить следующие закономерности:

Построение математической модели. Суммарные затраты на ранение, доставку и потери из-за неудовлетворенного спроса на период Т

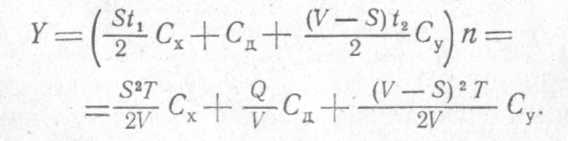
Исследование математической модели. Чтобы определить min функции, находим частные производные от Y по S и V и прирав­ниваем их к нулю

.

Решив систему уравнений, получим:

Sорт= √ (2*Q*C_д*C_x)/[T*C_x*(C_x+C_y)]; 2.1.

Vорт=√ (2*Q*C_д((C_x+C_y)/( T*C_x*Cy). 2.2.

2.2. Задания для самостоятельной работы

Определить оптимальную величину поставки S , и потребной партии V используя формулы 2.1.и.2.2., если известны следующие значения исходных данных(см. таблицу). Вариант задачи выбрать по номеру в журнале «Успеваемости посещаемости» студента.

Вариант	1	2	3	4	5	6	7	8	9	10	11	12
Затраты на хранение,Сх	3	4	5	6	7	8	9	7	6	5	4	3
Затраты на доставку,Сд	6	7	7	8	9	9	7	9	8	8	9	9
Месячная Потребность,Q	200	300	400	500	600	700	800	800	900	600	700	750
Период движения Запасов,Т	6	6	9	9	12	12	6	6	9	9	12	12
Убытки от неудов летворенного спроса, Су	7		7	7	7	8	8	8	9	9	9	7

Вариант	13	14	15	16	17	18	19	20	21	22	23	24
Затраты на хранение,Сх	3	4	5	6	7	8	9	7	6	5	4	3
Затраты на доставку,Сд	8	9	9	7	9	8	8	9	9	10	10	12
Месячная Потребность,Q	300	400	500	600	700	800	800	900	600	700	750	600
Период движения Запасов,Т	9	9	12	12	6	6	9	9	12	12	6	6
Убытки от неудов летворенного спроса, Су	8	8	8	9	9	9	6	6	6	5	5	5