3. Метод ітерації для рівнянь з одним невідомим

Переконаємося, що викладений в 2.8 метод простої ітерації уточнення коренів рівнянь з одним невідомим є окремим випадком описаного в 11.2 ітераційного процесу.

Розглянемо рівняння

(11.13)

з дійсною функцією . Корінь рівняння (11.13) є нерухомою точкою відображення . В якості метричного простору беремо або відрізок з області визначення функції (наприклад, відрізок ізоляції кореня t).

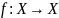Згідно з визначенням 11.3, функція стискаюча на з коефіцієнтом стиснення , якщо і

при всіх 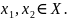(11.14)

Наступна теорема відповідає теоремі 11.1. У ній додатково наводиться властивість функції , що досить легко перевіряється, при наявності якої задовольняє умові Ліпшиця (11.14).

Теорема 11.2. Нехай:

1. функція відображає в себе;

2. функція диференційована на і існує число , таке, що

(11.15)

Тоді в існує єдиний корінь рівняння (11.13), який можна знайти як межу послідовності точок з , обумовленою рекурентною формулою

(11.16)

з будь-яким початковим наближенням . При цьому похибки наближень оцінюються за формулами:

(11.17)

(11.18)

○В силу теореми Банаха для доказу слід лише переконатися в тому, що з нерівності (11.15) випливає нерівність (11.14). Дійсно, нехай – будь-які дві точки з . Тоді, використовуючи теорему Лагранжа і співвідношення (11.15), одержимо

де – деяке число, що лежить між і .●

Таким чином, посилання на теорему Банаха дозволило довести нову (в порівнянні з теоремою 2.16 з п. 2.8.2) достатню умову застосування методу ітерації для наближеного розв'язання рівнянь з одним невідомим і отримати формули оцінки похибок наближень, які були незалежно виведені в 2.8 (див. теорему 2.16, яка доводиться в її умовах теорему 2.18 і впр. 2.41).

Порівнюючи теорему 11.2 з отриманими в 2.8 результатами, корисно звернути увагу на наступне. На відміну від теореми 11.2 в теоремі 2.16 не потрібно, щоб функція відображала в себе будь-який відрізок: виконання нерівності (11.15) на відрізку «потрійний довжини» і вибір початкового наближення з «серединного відрізка» забезпечують приналежність ітераційної послідовності відрізку та її збіжність до кореня . Отже, умови параграфа 2.8 є більш простими та зручними для перевірки.

Але, з іншого боку, результати, наведені в 2.8, отримані лише для випадку,коли метричним простором є відрізок, що істотно звужує можливості їх застосування. Тепер дано обґрунтування методу і при .

З урахуванням останнього факту отримаємо наслідок з теореми 11.2.

Наслідок 11.1. Якщо функція визначена і диференційована на і її похідна має властивість (11.15) на всьому , то рівняння (11.13) має один-єдиний корінь, а ітераційна послідовність (11.16) сходиться до нього, яке б число не було взято в якості початкового наближення.

Вправи

9. Покажіть, що для рівняння на відрізку виконані обидві умови теореми 11.2.

10. Нехай дано рівняння

1. Доведіть, що воно має корінь, причому тільки один.

2. Візьміть 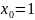, обчисліть , і за допомогою нерівності (11.18) знайдіть відрізок, де розташований корінь.

3. Переконайтеся в правильності результатів шляхом відділення коренів графічним методом.

9. В 11.2 зазначалося, що коли відображення не переводить множину в себе, збіжність ітераційної послідовності може залежати від вибору початкового наближення. Корінь рівняння , де

1. Покажіть, що функція не відображає в себе, але задовольняє на другій умові теореми 11.2.

2. Використовуючи геометричні побудови (див. 2.8), переконайтеся, що при ітераційна послідовність збігається до кореня, хоча не належить , а при 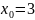вона розходиться.

Лекція 12