
- •Лекція № 11 стискаючі відображення і метод ітерації
- •Основні визначення
- •Принцип стискаючих відображень
- •Метод ітерації для рівнянь з одним невідомим
- •Метод ітерації для систем лінійних алгебраїчних рівнянь
- •Побудова ітераційної послідовності
- •Достатня умова збіжності ітераційної послідовності
- •Метод ітерації для систем нелінійних рівнянь
Лекція № 11 стискаючі відображення і метод ітерації
Одним з найбільш важливих інструментів математичного аналізу є теорема Банаха, яку називають також принципом стискаючих відображень. У цьому розділі теорема використовується для обґрунтування ітераційного методу наближеного розв'язку рівнянь з одним невідомим і систем рівнянь.
Основні визначення
В першій лекції було введено поняття метричного простору як деякої множини X із заданою на ньому метрикою (відстанню) ρ. Тим самим метричний простір являє собою пару (X, ρ), що складається з множини і відстані. Зміна будь-якого компонента цієї пари означає зміну метричного простору. Для стислості метричні простори будемо позначати так само, як і множини, за винятком випадків, коли зазначення відстані необхідно для конкретизації просторів.
Також
в
1.2
розглянуті
приклади
метричних
просторів,
серед
яких
простір
R
дійсних
чисел
з
метрикою,
яка визначається
за
формулою
(1.1),
і три
простори
n-мірних
дійсних
числових
векторів
Rn
з
метриками
(1.2)-(1.4).
Коли
необхідно підкреслити
вибір
відстані
в
просторах
векторів,
простір
Rn
з метрикою
ρ1,
будемо
позначати
через
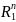 ,
з
метрикою
ρ2
–
,
з
метрикою
ρ2
–
 ,
з
метрикою
ρ∞
–
,
з
метрикою
ρ∞
–
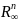 .
В
іншому
випадку
нижні
індекси
опускаємо.
.
В
іншому
випадку
нижні
індекси
опускаємо.
При
n=1
зазначені
метричні простори векторів є не чим
іншим, як простором R,
оскільки тоді вектори мають одну числову
координату, а всі ці три відстані між
одновимірними векторами
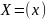 і
і
 рівні
рівні
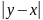 .
.
Простори
R, є основними
в даному розділі. Крім них знадобляться
і інші простори, що визначаються на їх
базі за такою схемою. Нехай X
—
метричний простір. Взявши будь-яку
підмножину множини X,
на ній природно ввести ту ж метрику
є основними
в даному розділі. Крім них знадобляться
і інші простори, що визначаються на їх
базі за такою схемою. Нехай X
—
метричний простір. Взявши будь-яку
підмножину множини X,
на ній природно ввести ту ж метрику
 ,
що і на X.
Тоді вийде новий метричний простір,
який називається метричним
підпростором
простору
X.
,
що і на X.
Тоді вийде новий метричний простір,
який називається метричним
підпростором
простору
X.
Наприклад, проміжки (0;1) і [0;3] можна вважати метричними підпросторами простору R, оскільки відстань між точками цих проміжків також визначається за формулою (1.1). У свою чергу, інтервал (0;1) є метричним підпростором відрізка [0;3].
З
курсу математичного аналізу відомо
поняття функції однієї або кількох
числових змінних, значеннями якої є
числа. Аналогічно визначається функція
 в разі довільних множин М
і N.
При цьому замість терміна «функція»
часто використовуються терміни
«відображення» чи «оператор». Якщо
в разі довільних множин М
і N.
При цьому замість терміна «функція»
часто використовуються терміни
«відображення» чи «оператор». Якщо
 ,
то елемент
,
то елемент
 називають образом
елемента х
при відображенні F.
Як і у випадку функцій, x
можна називати аргументом,
a F(x)
—
значенням
відображення F,
відповідним х.
називають образом
елемента х
при відображенні F.
Як і у випадку функцій, x
можна називати аргументом,
a F(x)
—
значенням
відображення F,
відповідним х.
Множина
М
називається областю
визначення відображення
F
(позначимо його DF),
а множина
 — множиною
значень
цього відображення.
— множиною
значень
цього відображення.
В цьому розділі мова піде про розв'язання рівнянь виду
 (11.1)
(11.1)
де
F
є відображенням, заданим на одному з
основних метричних просторів або на
якому-небудь їх підпросторі. Це рівняння
має сенс, якщо х
і F(x)
є або числами, або числовими векторами
однієї і тієї ж розмірності. Більш того,
завдання пошуку наближених рішень і
оцінки їх похибок вимагають, щоб відстані
між аргументами і між відповідними їм
значеннями вимірювалися однаково. Отже,
множина
значень відображення F
має бути підмножиною того ж основного
метричного простору, в якому знаходиться
її область визначення.
Не може бути, наприклад, рівняння виду
(11.1) з таким відображенням F,
що
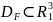 ,
а
,
а
 ,
або
,
або
 ,
а
,
а

У випадку коли F — дійсна функція однієї змінної, рівняння (11.1) являє собою рівняння з одним невідомим. Розглянуті в 12.1 та 12.2 наведені системи з п рівнянь з п невідомими є окремими випадками рівняння (11.1) з відображенням типу «вектор → вектор».
Визначення
11.1.
Елемент
 ,
при якому є правильною рівність
,
при якому є правильною рівність

називається розв’язком (коренем) рівняння (11.1).
Розв'язок
 рівняння (11.1) називають також нерухомою
точкою відображення F,
оскільки його образ
рівняння (11.1) називають також нерухомою
точкою відображення F,
оскільки його образ
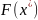 збігається з
.
збігається з
.
Приклад 11.1.
Функції
 відповідає рівняння виду (11.1):
відповідає рівняння виду (11.1):
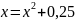 x.
Корінь х=0,5
цього рівняння є нерухомою точкою
функції
x.
Корінь х=0,5
цього рівняння є нерухомою точкою
функції
 .
.
Рівняння
 не має коренів, отже, у функції
не має коренів, отже, у функції
 нерухомих точок немає.
нерухомих точок немає.
При відображенні
 ,
що діє в просторі
,
що діє в просторі
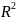 ,
отримаємо рівняння
,
отримаємо рівняння
 (у векторній формі), яке можна записати
у вигляді системи рівнянь (в координатній
формі)
(у векторній формі), яке можна записати
у вигляді системи рівнянь (в координатній
формі)

Нерухомою точкою даного відображення є вектор (0,0).
Нехай на R3 визначено відображення
 ,
де 0 = (0, 0, 0) – нульовий вектор. В цьому
випадку рівняння виду (11.1) скласти не
можна, бо в його лівій частині буде
тривимірний вектор, а в правій –
невід'ємне число. Зрозуміло, що у даного
відображення не може бути й нерухомої
точки.
●
,
де 0 = (0, 0, 0) – нульовий вектор. В цьому
випадку рівняння виду (11.1) скласти не
можна, бо в його лівій частині буде
тривимірний вектор, а в правій –
невід'ємне число. Зрозуміло, що у даного
відображення не може бути й нерухомої
точки.
●
Визначення
11.2.
Нехай
X
– метричний простір. Кажуть, що F
відображає
X
в себе, якщо
 ,
тобто образ F(x)
будь-якого елементу
,
тобто образ F(x)
будь-якого елементу
 належить цьому ж простору.
належить цьому ж простору.
Відображення,
що переводить в себе деякий основний
простір або його підпростір, володіє і
зазначеним вище властивістю, при якій
має сенс рівняння (11.1).
Зворотне, взагалі кажучи, невірно.
Дійсно, якщо раніше від заданого на
множині X
відображення F
було потрібно лише, щоб X
і множина його значень
 знаходилися в одному і тому ж основному
просторі, то тепер має бути
знаходилися в одному і тому ж основному
просторі, то тепер має бути
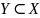 .
.
Специфіку
відображення метричного простору в
себе показує і такий факт: з
не випливає, що F відображає в себе кожну
підмножину
D
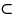 X.
X.
Приклад 11.2.
Дійсні
функції
 і
і
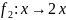 відображають у себе свою область
визначення R.
відображають у себе свою область
визначення R.
Нехай
тепер
 .
Оскільки
.
Оскільки
 ,
можемо сказати, що функція
,
можемо сказати, що функція
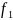 ,
відображає X
в себе. А от функція
,
відображає X
в себе. А от функція
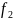 не відображає X
в себе, оскільки множина її значень
не відображає X
в себе, оскільки множина її значень
 дорівнює відрізку [-2,2].
Більш того,
не відображає у себе жоден відрізок
дорівнює відрізку [-2,2].
Більш того,
не відображає у себе жоден відрізок
 ,
крім одноточкового відрізка [0,0]
(переконайтеся в цьому!).
●
,
крім одноточкового відрізка [0,0]
(переконайтеся в цьому!).
●
Центральну роль надалі будуть відігравати наступні відображення.
Визначення 11.3. Нехай X – метричний простір. Задане на X відображення F називається стискаючим відображенням, або відображенням стискання на цьому просторі, якщо
F відображає X в себе;
F задовольняє на X умові Ліпшиця:
існує
число q,
 таке,
що
таке,
що
 для
всіх
для
всіх
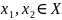 (11.2)
(11.2)
Число q при цьому називають коефіцієнтом стискання.
Помічаємо,
що нерівність (11.2) вимагає від відображення
стискання більш сильної властивості,
ніж та, при якій образи будь-яких двох
різних елементів
виявлялися на меншій відстані один від
одного, ніж.
 від
від
 Очевидно також, що коефіцієнт стискання
визначається неоднозначно. Якщо,
наприклад, нерівність (11.2) вірна при
Очевидно також, що коефіцієнт стискання
визначається неоднозначно. Якщо,
наприклад, нерівність (11.2) вірна при
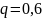 ,
то воно вірно і при будь-якому числі q з
пів інтервалу [0,6;1).
,
то воно вірно і при будь-якому числі q з
пів інтервалу [0,6;1).
Виконання наведених у визначенні 11.3 умов залежить як від особливостей відображення F, так і від простору, на якому воно розглядається. З цієї причини властивість стискання відображення, що має місце на X, зазвичай не поширюється на більшість його підпросторів. І навпаки, якщо відображення F володіє цією властивістю на якихось підпросторах X, воно може не виявитися стискаючим на всьому X.
Приклад 11.3.
Перевіримо,
чи буде відображення
 стискаючим на кількох обраних нами
метричних просторах.
стискаючим на кількох обраних нами
метричних просторах.
Нехай
 .
Зрозуміло, що функція
відображає R
в себе. З'ясуємо, чи задовольняє вона
умові Ліпшиця. По теоремі Лагранжа для
будь-яких двох різних точок
.
Зрозуміло, що функція
відображає R
в себе. З'ясуємо, чи задовольняє вона
умові Ліпшиця. По теоремі Лагранжа для
будь-яких двох різних точок
 маємо
маємо
 (11.3)
(11.3)
де
число c
лежить між
,
і
.
Якщо взяти
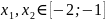 ,
то, оскільки
,
то, оскільки
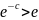 при всіх
при всіх
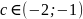 ,
отримаємо нерівність
,
отримаємо нерівність
 .
Це говорить про порушення умови Ліпшиця
на R
і, відповідно, про те, що дана функція
не є стискаючою на R.
.
Це говорить про порушення умови Ліпшиця
на R
і, відповідно, про те, що дана функція
не є стискаючою на R.
Тепер
візьмемо простір
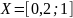 .
Функція
відображає обраний відрізок в себе, бо
для значення
.
Функція
відображає обраний відрізок в себе, бо
для значення
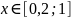 значення
значення
 .
Використовуючи рівність (11.3)
для довільних
.
Використовуючи рівність (11.3)
для довільних
 з цього відрізка,
будемо
мати
з цього відрізка,
будемо
мати

Значить,
відображення
 на даному просторі стискаюче, причому
коефіцієнтом
стиснення
можна вважати
на даному просторі стискаюче, причому
коефіцієнтом
стиснення
можна вважати
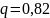 .
.
На
відрізку
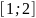 ця функція не буде стискаючою, хоча і
задовольняє на ньому
умові
Ліпшиця (перевірте останнє твердження!).
Справа в тому, що вона не відображає у
себе цей відрізок, оскільки жодне
значення
ця функція не буде стискаючою, хоча і
задовольняє на ньому
умові
Ліпшиця (перевірте останнє твердження!).
Справа в тому, що вона не відображає у
себе цей відрізок, оскільки жодне
значення
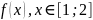 ,
не належить
[1;2].
●
,
не належить
[1;2].
●
Нарешті,
нам знадобиться поняття збіжності
послідовності
 елементів метричного простору
елементів метричного простору
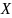 .
.
Визначення
11.4.
Кажуть, що послідовність
сходиться
до елементу
(записується:
 )
щодо
метрики
,
якщо
)
щодо
метрики
,
якщо
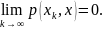 (11.4)
(11.4)
Елемент
 називається при цьому межею
послідовності
щодо
метрики
називається при цьому межею
послідовності
щодо
метрики
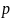 .
.
У
разі числових послідовностей умова
(11.4) означає:
 при
при
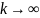 .
.
Коли
–
послідовність
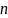 -мірних
векторів, в позначенні
-мірних
векторів, в позначенні
 -го
вектора індекс
будемо писати вгорі:
-го
вектора індекс
будемо писати вгорі:
 .
Можна показати, що послідовність векторів
у розглянутих нами
метричних
просторах сходиться до деякого вектора
тоді і тільки тоді, коли всі послідовності
координат
.
Можна показати, що послідовність векторів
у розглянутих нами
метричних
просторах сходиться до деякого вектора
тоді і тільки тоді, коли всі послідовності
координат
 ,
сходяться до відповідних координат
цього
вектора
(вправа 11.7).
Зважаючи на це, наприклад,
,
сходяться до відповідних координат
цього
вектора
(вправа 11.7).
Зважаючи на це, наприклад,
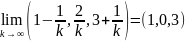
відносно
будь-якої з трьох метрик
 на
на
 .
.
Вправи
Покажіть, що функція відображає в себе
 ,
але не відображає у себе жоден відрізок
,
де
,
але не відображає у себе жоден відрізок
,
де
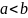 .
.Переконайтеся, що функція
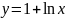 не відображає у себе область свого
визначення, проте є проміжки, які дана
функція переводить в себе.
Знайдіть
найбільший проміжок з такою властивістю.
не відображає у себе область свого
визначення, проте є проміжки, які дана
функція переводить в себе.
Знайдіть
найбільший проміжок з такою властивістю.Знайдіть множину значень заданого на відображення
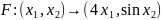 і переконайтеся, що
і переконайтеся, що
 відображає
в
себе.
відображає
в
себе.Покажіть, що відображення:



є стискаючими на своїх областях визначення.
1. Покажіть, що функція
 не є стискаючим відображенням на
відрізку
не є стискаючим відображенням на
відрізку

Знайдіть хоча б один відрізок, на якому дана функція буде стискаючою.
Нехай дано відображення
 безлічі двовимірних числових векторів
в себе, де
безлічі двовимірних числових векторів
в себе, де
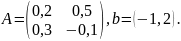
Напишіть формули обчислення координат вектора
 і знайдіть образ вектора
і знайдіть образ вектора
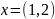 при цьому відображенні.
при цьому відображенні.Напишіть відповідну систему рівнянь виду (11.1).
Покажіть, що є відображенням стискання на

Нехай дана послідовність -мірних числових векторів
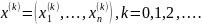 Доведіть, що збіжність послідовності
Доведіть, що збіжність послідовності
 до вектора
до вектора
 в просторах
рівносильна покоординатній збіжності:
в просторах
рівносильна покоординатній збіжності:
 при
всіх
при
всіх
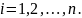
Знайдіть границю послідовності двовимірних векторів
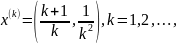 і визначте номер
,
починаючи з якого члени
і визначте номер
,
починаючи з якого члени
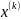 стають ближче ніж на
стають ближче ніж на
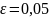 до цієї границі відносно відстаней
до цієї границі відносно відстаней

