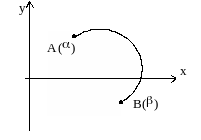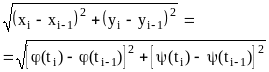1.7.8. Основная формула интегрального исчисления или формула Ньютона-Лейбница.

В разделе “Неопределенный интеграл” было показано, что любые две первообразные функции f(x) на сегменте [a,b] отличаются лишь на константу. В предыдущей теме данного пособия была доказана теорема, что интеграл с переменным верхним пределом F(x)= является одной из первообразных функции f(x) на сегменте [a,b] (с,х[a,b]), поэтому любая первообразная (х) непрерывной на сегменте [a,b] функции f(x) может быть представлена в виде , где с - произвольная постоянная. Используя свойство 1 определенного интеграла, имеем . Очевидно также, что при х=b , откуда .

Подставляя вместо с Ф(а) в последнее равенство, получим формулу

.

Для удобства записи разность  (b)- (а) записывают в форме , и - основная формула интегрального исчисления или формула Ньютона-Лейбница.

Примеры:

1.

2.

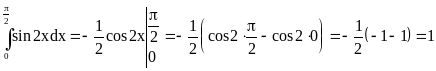
3.

4.

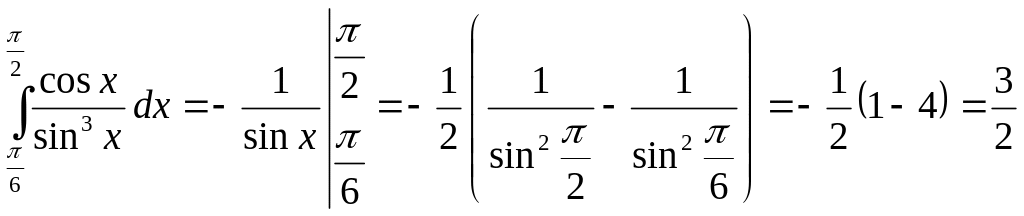
1.7.9. Формулы замены переменной и интегрирования по частям в определенном интеграле.

Теорема. Пусть функция f(x) непрерывна на сегменте [a,b]. Сегмент [a,b] является множеством значений некоторой функции x=g(t), определенной на сегменте   t  , причем g()=a, g()=b.

Пусть также непрерывна t [,]. Тогда справедлива формула: - формула замены переменной под знаком определенного интеграла.

Доказательство. Пусть  (x) - некоторая первообразная функции f(x), т.е. и . Так как функции  (х) и x=g(t) дифференцируемы на соответствующих сегментах, то сложная функция  [g(t)] дифференцируема на сегменте [,]. Применяя правило дифференцирования сложной функции, получим

(1)

где производная ' вычисляется по аргументу х: , где x=g(t). Так как , то при x=g(t) получим . Подставляя это значение в правую часть (1), получим , откуда следует, что [g(t)] на сегменте [,] является первообразной для функции . Поэтому по формуле Ньютона-Лейбница

,

а так как g()=b и g()=a, то окончательно получим

.

Пример 1. Рассмотрим 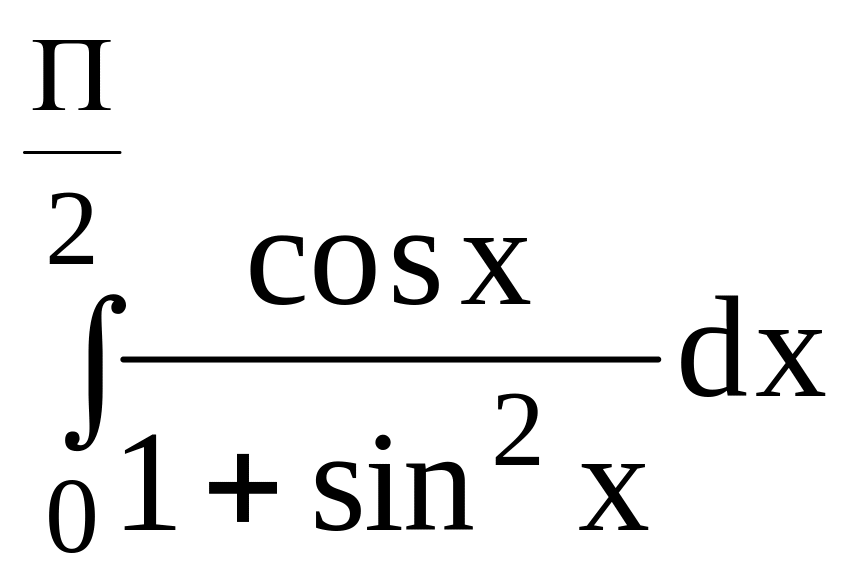. Положим sinx=t, и, следовательно, dt=cosxdx; так как t=0 при x=0 и t=1 при , то

.

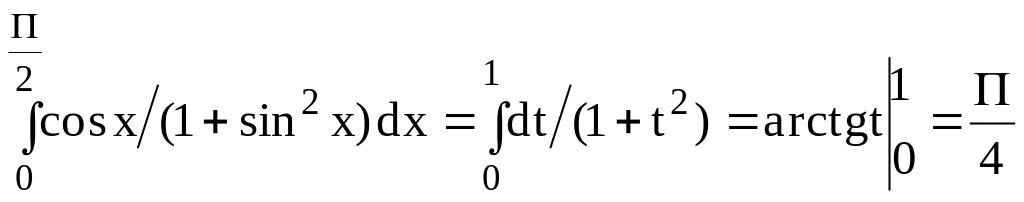Пример 2. Вычислить . Положим 1+х²=t, тогда dt=2xdx.

Поскольку t=4 при и t=9 при , то

.

Теорема. Если функции u(x) и v(x) на сегменте [a,b] имеют непрерывные производные, то справедлива следующая формула

,

которая называется формулой интегрирования по частям для определенных интегралов.

Доказательство. Поскольку , то функция u(x)v(x) является первообразной для функции , откуда следует, что . Используя свойства определенного интеграла, получим

.

Замечание. Так как и , то полученная формула может быть записана в виде .

Пример 1. Вычислить . Полагая u=x, dv=sinxdx, получим du=dx, v = -cosx, тогда

.

1.7.10. Спрямляемость и длина дуги плоской кривой.

Пусть заданы функции (t) и (t), непрерывные на сегменте [,]. Множество всех точек М, координаты х и у которых определяются уравнениями называется простой кривой, если различным значениям параметра t из сегмента [,] отвечают различные точки этого множества.

Будем называть точки А и В, отвечающие граничным значениям  и  параметра t, граничными точками простой кривой. Простой замкнутой кривой называется кривая L, которая образуется объединением двух простых кривых L1 и L2 следующим образом:

1) граничные точки кривой L₁, совпадают с граничными точками кривой L₂; 2) любые не граничные точки кривых L₁ и L₂ различны.

Определение. Пусть (t) и (t) непрерывны на . Уравнения

(1)

задают параметрически кривую L, если существует такая система сегментов , разбивающих множество , что для значений t из каждого данного сегмента этой системы уравнения (1) определяют простую кривую. При этом точки кривой L рассматриваются в определенном порядке в соответствии с возрастанием параметра t, т.е. если M₁ соответствует значению параметра t₁, а М₂ - t₂, то M₁ считаются предшествующей М₂, если t₁<t₂. Точки, отвечающие различным значениям параметра, всегда считаются различными.

Пример. Рассмотрим кривую L, задаваемую параметрически уравнениями

(2)

0  t  4. Это не простая кривая, но если взять систему сегментов [0, ], [,2], [2,3], [3,4], разбивающих [0,4], то для значений t из каждого

указанного сегмента данной системы уравнения (2) определяют простую кривую (полуокружность). Кривая L - дважды обходимая окружность.

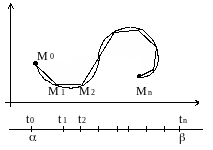
Итак, пусть кривая L задается параметрическими уравнениями . Пусть Т - произвольное разбиение [,] точками ₀=t₀<t₁<t₂<...<t_n = . Соответствующие точки кривой L обозначим через М₀, М₁, М₂, ..., М_n.

Ломаную M0M1M2...Mn будем называть ломаной, вписанной в кривую L и отвечающей данному разбиению Т сегмента [,]. Длина li звена Mi-1Mi этой ломаной равна

Длина всей этой ломаной равна

Определение. Если множество длин вписанных в кривую L ломаных, отвечающих всевозможным разбиением Т [,], ограничено, то кривая L называется спрямляемой. Точная верхняя грань l множества называется длиной дуги кривой L.

Теорема (о достаточных условиях спрямляемости и длине дуги плоской кривой). Если функции и имеют на сегменте [,] непрерывные производные, то кривая L, определяемая параметрическими уравнениями , спрямляема, и длина l ее дуги может быть вычислена по формуле

. (3)

Поясним без детального обоснования схему доказательства данной теоремы.

Этап 1. Рассматривается выражение

длины ломаной, вписанной в кривую L и отвечающей произвольному разбиению Т сегмента [,], и показывается ее ограниченность, т.е. кривая L - спрямляема. Длина кривой L обозначается через l.

Этап 2. Показывается, что сколь угодно мало отличается от величины при 0, где  - диаметр разбиения Т сегмента [,], а именно, . (4)

Этап 3. Показывается, что среди ломаных, длины которых удовлетворяют неравенству (4), имеются такие, длины которых мало отличаются от длины l дуги кривой L, а именно, 0<l- < .

Отсюда следует, что , и в силу произвольности 