1.7.5. Основные свойства определенного интеграла.

1) (по определению).

2) (по определению, при a<b).

3) (с = const).

4)

5) для произвольных с, при условии интегрируемости функции f(x).

6) если f(x) 0 x  [a,b].

7) Если функция f(x)  c[a,b], то свойство 6) можно уточнить при f(x)  0.

8) если f(x) g(x) x  [a,b].

9) .

10)

если

g(x) 0 x  [a,b], , .

1.7.6. Первая и вторая формулы среднего значения.

Докажем формулу, которая называется первой формулой среднего значения.

Пусть функции f(x) и g(x) интегрируемы на сегменте [a,b], и функция g(x) не меняет знака на этом сегменте. Если , , то существует число , удовлетворяющее неравенствам m    M, такое, что справедлива формула

. (1)

Если, в частности, f(x) непрерывна на сегменте [a,b], то [a,b], что будет выполняться равенство

. (2)

Замечание. Формула (1) (и (2)) называется первой формулой среднего значения.

Доказательство. Будем предполагать, что g(x)0 (в случае g(x)  0 рассуждения аналогичные).

а) Если , то в силу свойства 10 определенного интеграла (см. тему 5)

,

и тогда в качестве  можно взять любое число.

в) Пусть , тогда из 10)

.

Обозначая через , будем иметь формулу (1).

Формула (1) доказана.

Для доказательства формулы (2) нужно показать, что в случае непрерывной функции f(x) найдется такая точка [a,b], что f()= в формуле (1). Однако это вытекает из того, что непрерывная на сегменте [a,b] функция достигает на этом сегменте как своих точных граней M и m, так и любого промежуточного между ними значения  (m    M).

Следствие. В частном случае, когда g(x)1, формула (1) принимает вид:

,

а (в предположении непрерывности функции f(x) на сегменте [a,b]) формула (2) превращается в

Замечание. Если f(x) не является непрерывной, то формула (1) вообще говоря, неверна.

Пример.

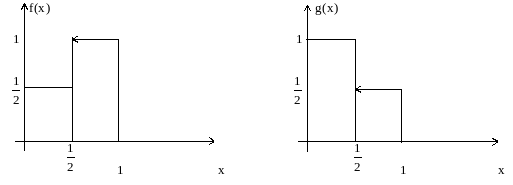
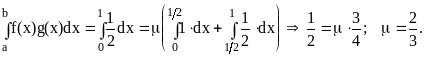
и для [0,1] f().

Сформулируем без доказательства теорему, позволяющую получить формулу, известную под названием второй формулы среднего значения, или формулы Бонне. Эта формула будет неоднократно использоваться в разных разделах математического анализа, в частности, в разделе “Несобственные интегралы”.

Теорема. Если на сегменте [a,b] функция g(х) монотонна, а f(x) интегрируема, то на этом сегменте существует такая точка , что

- вторая формула среднего значения или формула Бонне.

1.7.7. Интеграл с переменным верхним пределом.

Одним из важных понятий для непрерывных и интегрируемых на сегменте [a,b] функций является понятие интеграла с переменным верхним пределом, используя которое, можно получить основную формулу интегрального исчисления - формулу Ньютона-Лейбница.

Определение. Пусть функция f(x) интегрируема на любом сегменте [,](a,b) и пусть c - некоторая фиксированная точка, принадлежащая интервалу (a,b), тогда, каково бы ни было число х(a,b), функция f(x) интегрируема на [c,x], и на интервале (a,b) определена функция , которая называется интегралом с переменным верхним пределом.

Теорема. Любая непрерывная на интервале (a,b) функция f(x) имеет на этом интервале первообразную. Одной из первообразных является функция , где с - любая фиксированная точка интервала (a,b).

Достаточно доказать, что для (х берем таким, чтобы (х+х)(a,b)). Рассмотрим разность

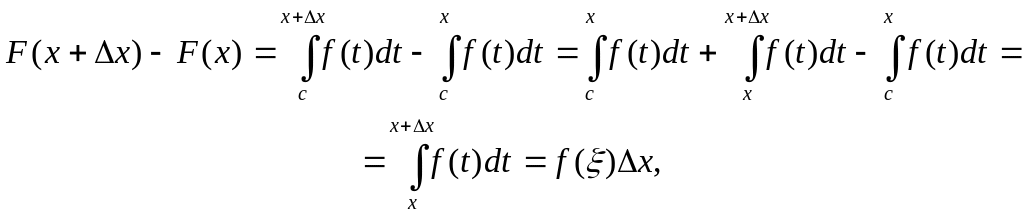
где  - некоторое число, заключенное между х и х+х (Здесь было использовано свойство 6 определенного интеграла и первая формула среднего значения для непрерывной на сегменте функции).

Так как f(x) непрерывна в точке х, то при х0 f()f(x), и поэтому .

Замечание 1. Аналогично доказывается теорема для непрерывной на сегменте [a,b] функции f(x). В этом случае в качестве с можно взять точку а и .

Замечание 2. Мы показали, что .

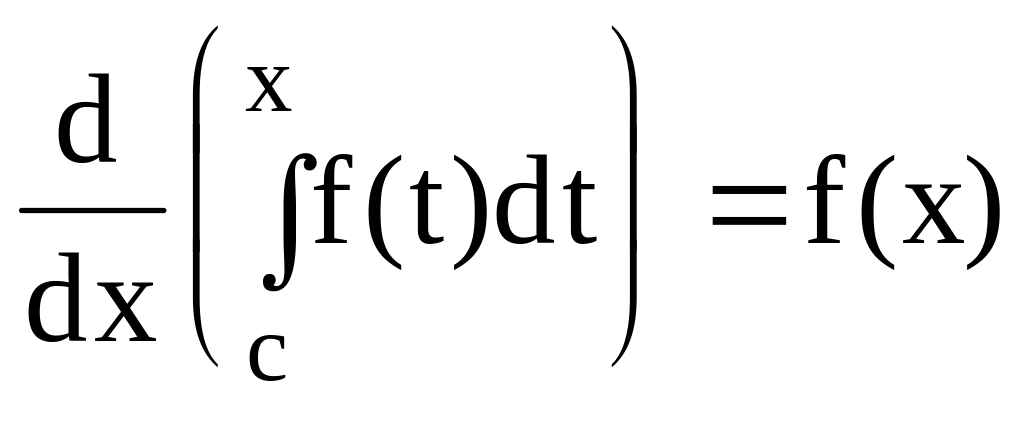Замечание 3. Если f(x) интегрируема на любом сегменте, содержащемся в интервале (a,b), то интеграл с переменным верхним пределом представляет собой непрерывную функцию на интервале (a,b) от верхнего предела. В самом деле

где m   M

Отсюда , и в силу разностной формы условия непрерывности F(x) есть непрерывная на интервале (a,b) функция.