- •1.7. Определенный интеграл и его геометрические приложения Для замечаний
- •1.7. Определенный интеграл и его геометрические приложения
- •1.7.1. Интегрируемость функции на сегменте.
- •1.7.2. Верхние и нижние суммы Дарбу и их свойства.
- •1.7.3. Необходимое и достаточное условие интегрируемости функции на сегменте.
- •1.7.4. Равномерная непрерывность функции на множестве.
- •1.7.5. Основные свойства определенного интеграла.
- •1.7.6. Первая и вторая формулы среднего значения.
- •1.7.7. Интеграл с переменным верхним пределом.
- •1.7.8. Основная формула интегрального исчисления или формула Ньютона-Лейбница.
- •1.7.9. Формулы замены переменной и интегрирования по частям в определенном интеграле.
- •1.7.10. Спрямляемость и длина дуги плоской кривой.
- •1.7.10.1. Вычисление длины дуги плоской кривой при различных способах ее задания.
- •1.7.11. Квадрируемость и площадь плоской фигуры.
- •1.7.12. Объем тела вращения.


1.7. Определенный интеграл и его геометрические приложения Для замечаний
1.7. Определенный интеграл и его геометрические приложения
1.7.1. Интегрируемость функции на сегменте.
Рис.1 |
Пусть
функция f(x) задана на сегменте [a,b]
(a<b). Обозначим че-
рез Т разбиение
[a,b] при помощи не совпадающих друг с
другом то-
чек a=x0<x1<...<xn=b
на n частич-
ных
сегментов
[x0,x1]...[xn-1,
xn].
Точки x0,x1,...,xn
называются точ-
ками разбиения Т.
Пусть
|
Определение 1.
Число
![]() ,
где
,
где
![]()
называется интегральной суммой функции f(x), соответствующей данному разбиению Т сегмента [a,b] и данному выбору промежуточных точек на частичных сегментах [xi-1,xi].
Обозначим
![]() - диаметр разбиения Т сегмента [a,b].
- диаметр разбиения Т сегмента [a,b].
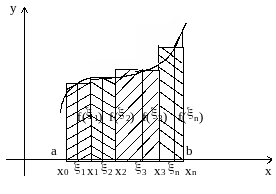
Геометрический смысл интегральной суммы . Рассмотрим криволинейную трапецию - фигуру, ограниченную графиком функции f(x) (будем считать ее положительной и непрерывной), двумя ординатами, проведенными в точках a и b оси абсцисс и осью абсцисс.
Интегральная сумма - площадь ступенчатой фигуры (рис.1).
Определение 2.
Число I
называется пределом интегральных сумм
при 0,
если для >0
можно указать такое положительное число
![]() ,
что для любого разбиения Т сегмента
[a,b], максимальная длина
частичных сегментов которого <,
независимо от выбора точек
на сегментах [xi-1,xi]
выполнено неравенство
,
что для любого разбиения Т сегмента
[a,b], максимальная длина
частичных сегментов которого <,
независимо от выбора точек
на сегментах [xi-1,xi]
выполнено неравенство
![]()
Если интегральная
сумма
при
0
имеет пределом число I, то будем записывать
это так
![]() .
.
Определение 3. Функция f(x) называется интегрируемой по Риману на [a,b], если существует конечный предел I интегральных сумм этой функции при 0. Указанный предел I называется определенным интегралом функции f(x) по [a,b] и обозначается так:
![]()
Из рисунка видно, что определенный интеграл численно равен площади криволинейной трапеции, определяемой графиком функции f(x) на [a,b].
Справедлива следующая теорема. Неограниченная на [a,b] функция f(x) не интегрируема на этом сегменте.
Доказательство:
Пусть функция
f(x) неограничена на [a,b], тогда она
неограничена на некотором частичном
сегменте [xk-1,xk]
любого данного разбиения Т сегмента
[a,b]. Тогда слагаемое f(![]() )xk
интегральной суммы
,
отвечающее этому разбиению Т, за счет
выбора т.
может быть сделано как угодно большим
по абсолютной величине, т.е. интегральные
суммы
,
отвечающие любому разбиению Т, не
ограничены, и поэтому не существует
конечного предела интегральных сумм.
Итак, будем рассматривать лишь ограниченные
на [a,b] функции.
)xk
интегральной суммы
,
отвечающее этому разбиению Т, за счет
выбора т.
может быть сделано как угодно большим
по абсолютной величине, т.е. интегральные
суммы
,
отвечающие любому разбиению Т, не
ограничены, и поэтому не существует
конечного предела интегральных сумм.
Итак, будем рассматривать лишь ограниченные
на [a,b] функции.
Замечание: Отметим, что вообще говоря, не всякая ограниченная на [a,b] функция является интегрируемой на этом сегменте.
Проверьте это положение для функции Дирихле (значения в рациональных точках 1, а в иррациональных - 0). Эта функция не интегрируема на [a,b].
1.7.2. Верхние и нижние суммы Дарбу и их свойства.
Пусть функция f(x) - ограниченная на [a,b] функция, т.е. (m,M) (x[a,b]):[m f(x) M]. Т - разбиение [a,b] точками a=x0<x1<...<xn=b.
Обозначим через Mi - точную верхнюю и через mi - точную нижнюю грани этой функции на [xi-1,xi].
Суммы ![]()
![]()
называются верхней и нижней суммами функции f(x) для данного разбиения Т сегмента [a,b].
Заметим, что любая интегральная сумма данного разбиения Т сегмента [a,b] заключена между верхней и нижней суммами S и s этого разбиения.
Геометрический смысл верхней и нижней сумм. Рассмотрим для простоты положительную и непрерывную функцию f(x) и криволинейную трапецию, определяемую этой функцией.

Рис.1 Рис.2
Mi и mi в случае непрерывности функции представляют собой максимальное и минимальное значения этой функции на частичном сегменте [xi-1,xi] разбиения Т, S и s - площади заштрихованных ступенчатых фигур, изображенных на рисунках 1 и 2 соответственно.
Свойства верхних и нижних сумм подробно изложены в [2] (стр. 321-323), поэтому приведем лишь формулировки теорем и прокомментируем каждую из них с помощью рисунков.
Свойство 1. Для любого фиксированного разбиения Т и для любого >0 промежуточные точки на сегментах [xi-1,xi] можно выбрать так, что интегральная сумма будет удовлетворять неравенствам 0S- <. Точки можно выбрать и таким образом, что интегральная сумма будет удовлетворять неравенствам 0 -s<.
Рис. 3 |
На рисунке 3 изображен графикфункции f(x), заданной на сегменте [a,b]. - промежуточные точки на частичных сегментах [xi-1,xi] Преобразуем разность S- = M1x1
+ M2x2
+... Mixi
+...+
Mnxn
--
f( -f(
)xi
-...- f( =
[M1-f( +[Mi-
f(
)]xi+...+[Mn-
f( |
Здесь S - верхняя сумма. Каждое слагаемое последней суммы представляет собой площадь заштрихованного прямоугольника, поэтому S- есть сумма площадей заштрихованных прямоугольников, которая, очевидно, может быть сколь угодно уменьшена за счет выбора точек (если промежуточные точки выбирать близкими к точкам сегментов [xi-1,xi], в которых функция f(x) принимает значения Mi).
Для нижних сумм рассуждения проводятся аналогичным образом.
Свойство 2. Если
разбиение
![]() сегмента
[a,b] получено путем добавления новых
точек к точкам разбиения Т этого сегмента,
то верхняя сумма
сегмента
[a,b] получено путем добавления новых
точек к точкам разбиения Т этого сегмента,
то верхняя сумма
![]() разбиения
разбиения
![]() не больше (
S)
верхней суммы S разбиения Т, а нижняя
сумма
не больше (
S)
верхней суммы S разбиения Т, а нижняя
сумма
![]() разбиения
не меньше (s
)
нижней суммы s разбиения Т.
разбиения
не меньше (s
)
нижней суммы s разбиения Т.

Рис. 4 Рис. 5
На рис. 4 точки x0, x1, x2, x3 - точки разбиения сегмента [a,b], соответствующие разбиению Т. Кружками отмечены новые точки t1, t2, которые вместе с точками xi дают новое разбиение сегмента [a,b].
Сегменты [x0,x1] и [x2,x3] поделились на сегменты [x0,t1], [t1,x1] и [x2,t2], [t2,x3], соответственно. Верхняя сумма на сегментах [x0,t1] и [x2,t2] уменьшилась на величину, равную площадям прямоугольников ABCD и KLMN, а на остальных частичных сегментах осталась без изменения, поэтому верхняя сумма разбиения уменьшилась по сравнению с верхней суммой S.
На рис.5 приведена аналогичная картина для нижних сумм.
Свойство 3. Пусть
и
![]() любые два разбиения [a,b]. Тогда нижняя
сумма одного из этих разбиений не
превосходит верхнюю сумму другого.
Именно, если
,
;
любые два разбиения [a,b]. Тогда нижняя
сумма одного из этих разбиений не
превосходит верхнюю сумму другого.
Именно, если
,
;
![]() ,
,![]() соответственно нижние и верхние суммы
разбиений
и
,
то
;
<
.
соответственно нижние и верхние суммы
разбиений
и
,
то
;
<
.
Рис.6 |
На рис. 6 одинарной штриховкой показана верхняя сумма разбиения сегмента [a,b] точками x0=a<x1<x2<x3=b, а двойной штриховкой - нижняя сумма разбиения сегмента [a,b] точками 0=a<1<2<3<4=b |
Свойство 4.
Множество
![]() верхних сумм данной функции f(x) для
всевозможных разбиений сегмента [a,b]
ограничено снизу. Множество
верхних сумм данной функции f(x) для
всевозможных разбиений сегмента [a,b]
ограничено снизу. Множество
![]() нижних сумм ограничено сверху.
нижних сумм ограничено сверху.
Обозначим через
![]() точную нижнюю грань множества
верхних сумм
точную нижнюю грань множества
верхних сумм
![]() ,
а через
,
а через
![]() точную верхнюю грань множества
нижних сумм
точную верхнюю грань множества
нижних сумм
![]() .
Числа
и
называются соответственно нижним и
верхним интегралами Дарбу от функции
f(x). Легко показать, что
.
Числа
и
называются соответственно нижним и
верхним интегралами Дарбу от функции
f(x). Легко показать, что
![]()
Свойство 5. Пусть разбиение [a,b] получено из разбиения Т добавлением к последнему р новых точек, и пусть , ; s, S - соответственно нижние и верхние суммы разбиений и Т. Тогда для разностей S- и -s может быть получена оценка, зависящая от максимальной длины частичных сегментов разбиения Т, числа р добавленных точек и точных верхней и нижней граней М и m функции f(x) на сегменте [a,b], а именно: S- (M-m)р и -s (M-m)р

Рис.7
На рис.7 точки x0 = a < x1 < x2 < x3 < x4 = b соответствуют разбиению Т сегмента [a,b], а две добавленные точки 1 и 2 образуют вместе с точками xi: x0=a<1<x1<x2<2<x3<x4=b разбиение этого сегмента.
Одинарной штриховкой показана верхняя сумма S разбиения Т, а двойной штриховкой два прямоугольника, сумма площадей которых дает уменьшение S до величины . Если через М и m обозначить точные верхнюю и нижнюю грани функции f(x) на [a,b], а через максимальную длину частичного сегмента [xi-1,xi] разбиения Т, то площадь прямоугольника ABCD, равная (M-m)x будет больше площади каждого из двух прямоугольников, заштрихованных двойной штриховкой, отсюда очевидна оценка: S- (M-m)2 (здесь 2 - число добавленных точек). Для нижних сумм может быть дана аналогичная интерпретация.
В заключение данной темы приведем без доказательства формулировку теоремы, известной под названием леммы Дарбу, имеющей фундаментальное значение для построения теории в теме “Определенный интеграл”.
Лемма Дарбу.
Верхний и
нижний интегралы Дарбу
и
от функции f(x) по сегменту [a,b] являются
соответственно пределами верхних и
нижних сумм при 0,
т.е.
![]() и
и
![]() .
.
Замечание 1. Число
,
например, называется пределом верхних
сумм S при 0,
если
![]() .
.
Замечание 2. В
случае, когда
=
=
I лемма Дарбу позволяет переходить к
пределам в неравенствах вида
![]() при стремлении к нулю диаметра
разбиения Т сегмента [a,b]. При этом sI
и SI,
откуда
при стремлении к нулю диаметра
разбиения Т сегмента [a,b]. При этом sI
и SI,
откуда
![]() .
.