1.1.1.9. Декартова прямоугольная система координат в пространстве. (дпск)

ДПСК является частным случаем аффинной системы, отвечающим тройке взаимно ортогональных и единичных базисных векторов . Принято направления векторов брать совпадающими с направлением декартовых осей Ox, Oy, Oz соответственно.

Нами получено, что любой вектор может быть, причем единственным способом, разложен по декартову прямоугольному базису (ДПБ) , т.е. для каждого вектора существует единственная тройка чисел X, Y, Z такая, что

.

Числа X, Y, Z называются декартовыми прямоугольными координатами (ДПК) вектора . Если M- любая точка пространства, то ДПК этой точки совпадают с ДПК вектора .

Вектор будем также записывать в виде .

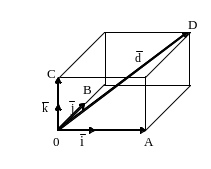
Теорема 1.9. ДПК вектора равны прекциям этого вектора на оси OX, OY и OZ соответственно.

Доказательство.

. , т.к. из и того, что , получаем . Но знаки OA и X совпадают,

т.к. когда векторы направлены в одну сторону, оба числа OA и X положительны, а в случае когда векторы направлены в противоположные стороны, оба числа OA и X отрицательны. Т.е. OA=X.

Аналогично OB=Y, OC=Z, ч.т.д.

Обозначим , ,  углы наклона вектора к осям Ox, Oy, Oz соответственно. Числа cos, cos, cos называют направляющими косинусами вектора .

Из теорем 8 и 9 имеем

. (1)

Т.к. квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его сторон, то из равенств OA=X, OB=Y, OC=Z получим выражение для длины вектора через его координаты:

(2)

Из формул (1) и (2) имеем:

, .

Возводя в квадрат и складывая последние равенства, получим

.

24