Контрольные вопросы:

1. На чем основан выборочный метод?

2. Понятие вариационного ряда. Как строится дискретный и интервальный вариационный ряд?

3. Геометрическое представление вариационного ряда: полигон и гистограмма распределения частот (или относительных частот).

4. Выборочные характеристики вариационного ряда: , D_B, S², m, M_o, M_e, V, p. Что они характеризуют?

11.2 Статистические оценки параметров распределения

Параметры распределения – это характеристики функции плотности распределения случайной величины. Например, для нормального закона распределения, задаваемого плотностью распределения:

параметрами служат: a – математическое ожидание, - среднеквадратическое отклонение.

Статистической оценкой неизвестного параметра теоретического распределения называется его приближенное значение, зависящее от данных выборки, то есть от:

x₁, x₂, … x_k - значений признака,

n₁, n₂, … n_k – соответствующих им частот.

Обозначим - оцениваемый параметр теоретического распределения,

- его статистическая оценка для некоторой выборочной совокупности.

Величину называют точностью оценки. Чем она меньше, тем точнее определен неизвестный параметр. Практическую ценность статистической оценки характеризуют – отсутствие систематической ошибки и минимально возможное значение дисперсии.

Оценка параметра называется несмещенной, если ее математическое ожидание равно оцениваемому параметру, то есть (в противном случае, оценка – «смещенная»).

Например, при «смещенном» значении показаний прибора, необходима его калибровка.

Оценка называется состоятельной, если

То есть оценка сходится по вероятности к .

Оценка параметра называется эффективной, если при заданном n она обладает наименьшей дисперией.

Теорема: Выборочная средняя является несмещенной и состоятельной оценкой математического ожидания a.

Исправленная выборочная дисперсия является несмещенной и состоятельной оценкой дисперсии D(X).

Доверительные интервалы и доверительные вероятности.

Вероятность выполнения неравенства называется доверительной вероятностью или надежностью оценки параметра :

.

Случайный интервал , в пределах которого с вероятностью находится неизвестный оцениваемый параметр, называется доверительным интервалом I, соответствующим коэффициенту доверия ,

Если задан доверительный интервал, то может возникнуть задача определения надежности оценки. И обратно, при заданной надежности оценки , в соответствии с законом распределения случайной величины, можно найти доверительный интервал I.

Если, например, , то показывает вероятность ошибки надежности оценки, р – уровень значимости оценки. Обычно берут р = 0,05; 0,01; 0,001.

Доверительный интервал для математического ожидания нормально распределенного признака.

1) Предположим, среднее квадратическое отклонение известно (например, если измерения производятся одним и тем же прибором при одних и тех же условиях). Случайная величина Х распределена нормально с параметрами а и . Построим доверительный интервал, покрывающий неизвестный параметр а с заданной надежностью . Данные выборки есть реализации случайных величин Х₁, Х₂,…Х_п, имеющих нормальное распределение с параметрами а и . Оказывается, что и выборочная средняя случайная величина тоже имеет нормальное распределение (примем без доказательства). При этом:

Потребуем, чтобы выполнялось где - заданная надежность. Используя известную формулу для нормально распределенной случайной величины , получим: , где, в данном случае, . Окончательно имеем:

Таким образом с надежностью можно утверждать, что доверительный интервал покрывает неизвестный параметр а с точностью оценки Здесь параметр t определяется из равенства по таблице приложения 1.

2) В случае малой выборки (п<30), при неизвестных параметрах а и , функция распределения нормированной случайной величины:

( ),

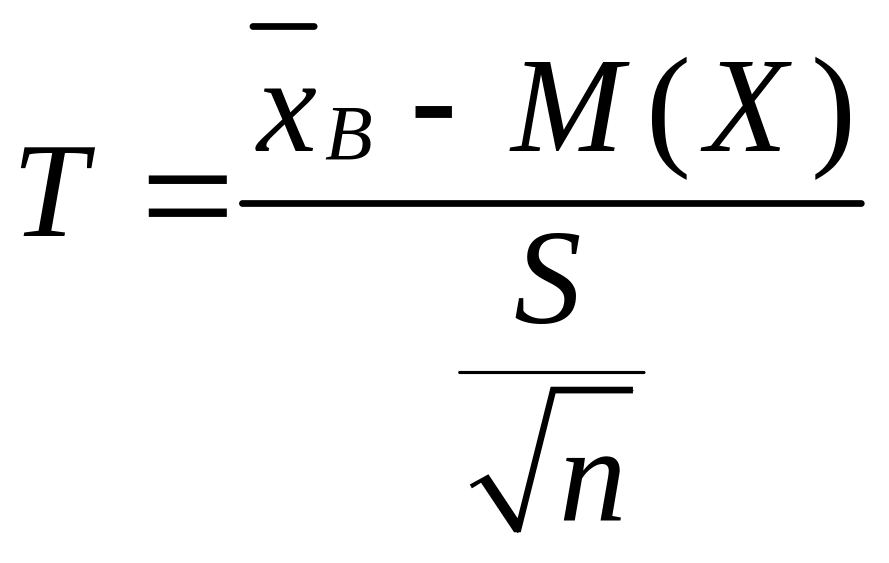зависит только от объема выборки и задается t- распределением Стьюдента с п-1 степенями свободы . Эта формула связывает случайную величину Т, доверительный интервал I и доверительную вероятность . Откуда, подставляя Т : .

Параметр задается в соответствии с таблицей Стьюдента (приложение 3).

Для больших п (n>30) значения параметров t и практически совпадают.

Пример 1. При измерении длины колоса ячменя, в соответствии с данными выборки составлен интервальный вариационный ряд:

-длина колоса,см	7-8	8-9	9-10	10-11	11-12	12-13	13-14
- частота	4	10	14	12	5	4	1

(п= =50).

Требуется: оценить значения параметров статистического распределения, а также границы доверительного интервала, в котором с вероятностью 0,95 (или с надежностью 95%) заключено значение средней длины колоса по генеральной совокупности.

1) Рассчитаем значение выборочной средней :

(см).

2) Рассчитаем значение исправленной дисперсии:

Откуда исправленное среднеквадратическое

3) Для расчета границ доверительного интервала, подсчитаем предварительно точность оценки Параметр t принимается исходя из значений для интегральной функции Лапласа (таблица 1 Приложения) и исходя из требуемой надежности оценки: . Тогда .

Границы доверительного интервала:

(левая граница);

(правая граница).

Таким образом, с надежностью 95% можно утверждать, что, что среднее значение длины колоса (по генеральной совокупности) заключено в пределах – от 9,5 до 10,3 (см).

Доверительный интервал для оценки среднеквадратического отклонения в случае нормального распределения.

Теорема: Для нормально распределенной случайной величины Х выполняется:

,

где - доверительная вероятность, зависящая от объема выборки п и точности оценки (примем без доказательства).

Из неравенства следует: .

То есть, с надежностью можно утверждать, что доверительный интервал покрывает неизвестный параметр с точностью оценки

Для примера 1 найдем доверительный интервал, покрывающий неизвестное значение среднеквадратического с вероятностью

1. По таблице (приложение 4) находим значение .

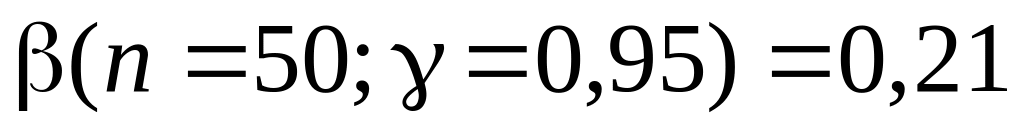2. Найдем границы доверительного интервала:

Левая граница:

Правая граница:

Таким образом, с надежностью 95% можно утверждать, что среднеквадратическое отклонение длины колоса заключено в пределах, от 1,14 до 1,74.

Задачи для самостоятельного решения:

1. Для задачи 1 (раздела 11.1) найти границы доверительного интервала, к котором с вероятностью 0,95 заключено среднее значение (числа отелов) по генеральной совокупности.

2. Для задачи 2 (раздела 11.1) найти границы доверительного интервала, в котором с вероятностью 0,99 заключено: а) среднее значение (массы клубня) по генеральной совокупности; б) значение среднеквадратического отклонения.

Контрольные вопросы:

1. Что называется статистической оценкой неизвестного параметра теоретического распределения? В каком случае оценка является: а) несмещенной, б) состоятельной, в) эффективной?

2. Что называется доверительной вероятностью и доверительным интервалом неизвестного оцениваемого параметра?

3. Как оценить границы доверительного интервала для математического ожидания нормально распределенного признака?

4. Как оценить границы доверительного интервала для среднеквадратического отклонения нормально распределенного признака?