Лекція

Тема Розрахунки розімкнутих місцевих мереж

6-1. Допустимі втрати напруги в лініях місцевих мереж

Джерелом живлення місцевих мереж є або шини генераторної напруги електричних станцій, або шини вторинної напруги (6-10-35 кВ) районних підстанцій і станцій. Передача електричної енергії від джерел живлення до електроприймачів супроводжується втратою напруги в лініях і трансформаторах, тому в споживачів напруга не зберігає свого постійного значення.

Розрізняють відхилення напруги, обумовлені процесами, що повільно протікають, зміни навантажень в окремих ланках мережі, змінами режимів на джерелах живлення, змінами навантажень споживачів, у результаті чого протягом року і навіть доби в окремих точках мережі напруга ­міняється по величині, відхиляючись від номінального значення; коливання напруги - швидко протікаючі (зі швидкістю не менше 1% у секунду) короткочасні зміни напруги, що виникають при різких порушеннях нормального режиму мережі, наприклад при включенні потужних електроприймачів, при змінному режимі їх роботи, при коротких замиканнях у мережі і т.д.

Щоб забезпечити нормальну роботу електроприймачів, до них треба підводити напругу, близьку по величині до їхньої номінальної напруги. Якщо ж дійсна напруга значно відхиляється від номінальної, то робота електроприймачів може порушитись. Наприклад, для ламп розжарювання зниження напруги на 10% викликає зниження світлового потоку приблизно на 30%, а перевищення номінальної напруги на 5% приводить до скорочення терміну служби ламп приблизно вдвічі. В люмінесцентних лампах залежність світловіддачі від напруги виражена не настільки різко, як у ламп розжарювання (так, зниження напруги на 1% зменшує світловий потік люмінесцентних ламп тільки на 1,25%), однак запалювання їх сильно залежить від стабільності напруги в мережі. В електродвигунах, як відомо обертальний момент залежить від квадрата напруги, тому при зниженому рівні напруги суттєво знижується продуктивність механізмів, а при постійному моменті опору відбувається перевантаження двигуна по струму. Одночасно знижується коефіцієнт потужності установки.

Відхилення напруги виражається у відсотках номінальної напруги:

.

і коливання напруги:

ГОСТ 13109-97 встановлені наступні припустимі відхилення напруги:

а) на затискачах електродвигунів і апаратів їх пуску і керування в межах від мінус 5 до плюс 10% від номінальної напруги;

б) на затискачах приладів робочого освітлення, установлених у виробничих приміщеннях і громадських будівлях, а також у прожекторних установах зовнішнього освітлення в межах від мінус 2,5 до плюс 5% від номінальної напруги;

в) на затискачах інших приймачів електричної енергії в межах ±5% від номінальної напруги.

У після аварійних режимах допускається додаткове зниження напруги на 5% до зазначених вище по ГОСТ 13109-67.

В електричних мережах сільськогосподарського призначення і у мережах тягових підстанцій, що харчуються від шин, допускаються великі значення відхилення напруги (наприклад, при перерізі проводів мережі, обраних по економічній щільності струму, повинен забезпечуватися відхилення напруги в споживачів у межах від +7,5 до —10% від номінального).

Припустимі коливання напруги на затискачах освітлювальних ламп і радіоприладів залежить від частоти коливань. Виражена у відсотках, понад допустиме відхилення напруги, допустима величина коливань визначається за формулою:

де n — число коливань у годину.

Щоб забезпечити подачу до приймачів напруги належної величини, тобто не перевищуючої зазначених вище меж, у мережі проводять наступні заходи:

а) застосовують трансформатори з коефіцієнтами трансформації, що враховують втрату напруги як в обмотках трансформаторів, так і в мережі яка живиться ними; крім того, обмотки вищої напруги трансформаторів постачаються відгалуженнями, що дозволяють міняти коефіцієнт трансформації в деяких межах;

б) встановлюють трансформатори із пристосуваннями для регулювання напруги під навантаженням, а також інше обладнання, для компенсації втрати напруги в мережі;

в) схему, номінальну напругу мережі і переріз провідників ліній, що живлять споживачів, вибирають таким чином, щоб втрата напруги в них не перевищувала допустимої величини.

Задача розрахунків мереж по втраті напруги полягає у визначенні рівнів напруги в споживачів з обліком усіх зазначених вище факторів і добових коливань навантаження в лініях і напруги на джерелах живлення.

Під втратою напруги розуміють алгебраїчну різницю між абсолютними значеннями напруги в розглянутих точках мережі (ліній).

Критерієм правильності вибору перерізу проводів на окремих ділянках мережі є забезпечення допустимих значень напруг у споживачів в різних режимах.

Для проведення таких розрахунків треба визначити втрату напруги окремо в живильній мережі, у трансформаторах і в розподільній мережі для різних режимів роботи мережі (наприклад, при максимальних і мінімальних навантаженнях), а потім шляхом добору коефіцієнтів трансформації і меж їх регулювання прийняти правильне рішення.

Практика показує, що розрахунки місцевих мереж, проведені з врахуванням усіх зазначених вище факторів - справа досить трудомістка і складна, і до того ж, не завжди дає точні результати, особливо при наявності у споживачів різнорідних графіків на­вантаження, вплив яких не завжди можна врахувати. Тому віддають перевагу розрахункам місцевих мереж спрощеним способом, а саме по припустимій втраті напруги, встановленої з деяким ступенем точності для різних категорій і видів мереж, виходячи з нормованих значень відхилень напруг на приймачах. Такий метод цілком виправданий для практичних цілей, тому що між відхиленнями напруги і втратами напруги існує тісна залежність, яку можна визначити для ряду конкретних випадків із врахуванням згаданих вище заходів щодо добору і регулюванню коефіцієнтів трансформації трансформаторів.

При проведенні розрахунків даним способом застосовні наступні допустимі величини втрат напруги:

а) для мереж напругою 220 і 380 В на всій їх протяжності, починаючи від шин ТП і до останнього приймача, - від 5 до 6,5%, з них у внутрішньо-квартирній мережі і у груповій мережі квартир - від 1 до 2,5%;

б) для живильної мережі напругою 6-35 кВ - від 6 до 8% у нормальних режимах і від 10 до 12% в аварійних;

в) для сільських мереж напругою 6-35 кВ із метою їх здешевлення допускається мати втрату напруги в нормальних режимах до 10%.

Напруга на ділянках ліній, розташованих близько до джерел живлення, виходить вища, а на ділянках, віддалених від джерел живлення, — нижча номінальної. Щоб на вторинній стороні трансформаторів, включених у цих місцях у мережу, одержати напругу необхідного рівня, треба відповідним чином підібрати відгалуження на обмотках трансформаторів. У місцях з підвищеним рівнем напруги встановлюють більший коефіцієнт трансформації (+2,5% або 5%), а в місцях зі зниженою напругою - менший (-2,5% або -5%).

Наведені вище допустимі втрати напруги в лініях підібрані так, щоб при належному регулюванні напруги на джерелах живлення і при правильному виборі відгалужень на обмотках мережних трансформаторів задовільнялися вимоги ПУЕ відносно відхилень напруги на приймачах електричної енергії.

З метою усунення похибок, пов'язаних із застосуванням методу розрахунків по припустимій втраті напруги, рекомендується у всіх можливих випадках вести розрахунки спільно для розподільних мереж середньої (6-10 кВ) і низької (0,38 кВ) напруги. Втрату напруги в опорі мережних трансформаторів при цьому можна прийняти рівною 2,5-3%, що відповідає повному навантаженню -трансформатора при коефіцієнті потужності навантаження споживачів 0,92-0,87.

До сказаного слід додати, що вибір перерізу проводів повинен бути обґрунтований зіставленням техніко-економічних показників (див. § 4-4).

6-2. Визначення втрати напруги і перерізів проводів у лініях постійного струму і в освітлювальних двопровідних лініях змінного струму

Прикладом найпростішого розрахунку мережі за умовами припустимих втрат напруги може служити двопровідна лінія постійного струму.

На мал. 6-1, а наведена схема для загального випадку такої лінії.

В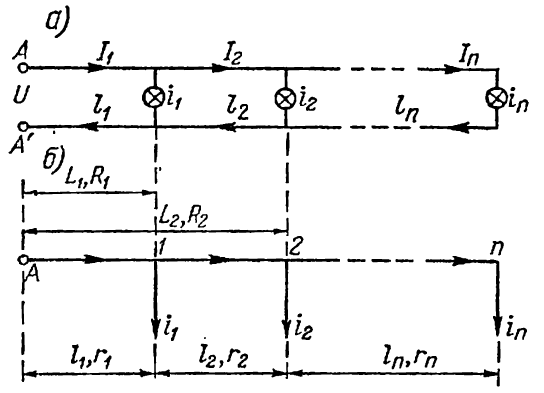 ід точок А і А' джерела струму з напругою U живиться лінія з навантаженнями і₁, і_{2, ...,} і_n. Відстані між навантаженнями позначені через l₁, l₂, ...,l_n а струми в проводах – через І₁, І₂ ,...,І_n .

На мал. 6-1,б ця ж схема представлена в спрощеному вигляді в однолінійному зображенні. Тут струми в проводах показані по направленню від джерела струму до навантажень, зворотні проводи і відповідно струми в них не показані.

Визначимо, користуючись законом

Рис. 6-1. Схема двопровідної лінії Ома, падіння напруги між точками А і n лінії як суму спадань напруги на всіх ділянках лінії в прямому і зворотному проводах:

(6-1)

або

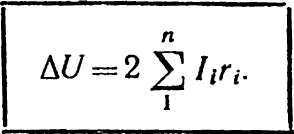(6-2)

Так як звичайно задані струми навантаження і₁, і_{2, ...,} і_n, а струми в лінії І₁, І₂,...,І_n невідомі, то зручно виведену формулу перетворити, замінивши лінійні струми струмами навантаження і використавши закон Кірхгофа для кожного вузла:

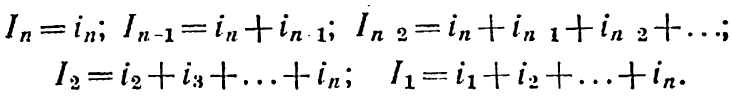
Підставивши ці значення у формулу (6-1):

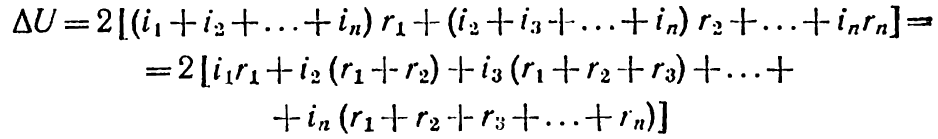
і замінивши, згідно з позначеннями на мал. 6-1,

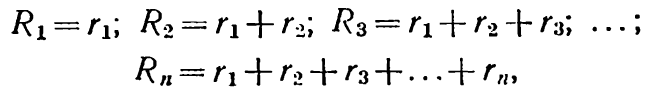
отримаємо

(6-3)

або

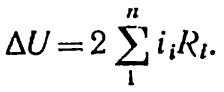(6-4)

Обчислену по формулах (6-2) і (6-4) втрату напруги треба порівняти із гранично допустимою (ΔU_доп) у вольтах або у відсотках від U_н:

Слід зазначити, що формула (6-2) є найбільш зручною для розрахунків мереж, переріз проводів яких вибирається по економічній щільності струму і особливо в тому випадку, коли він є змінним уздовж лінії по ділянках.

Для визначення залежності між втратою напруги і перетином лінії F замінимо у формулах (6-2) і (6-4):

де l_і – довжини ліній між навантаженнями; 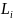L_і – відстані від джерела живлення до кожного навантаження (див. мал. 6-1,б); ρ – питомий опір проводу.

В результаті зазначеної заміни запишемо:

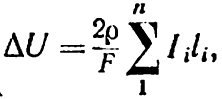(6-5)

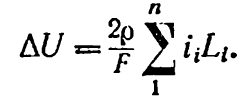(6-6)

Ці формули зручні для розрахунків мереж із проводами однакового перерізу по їхній довжині. По них можна визначити втрату напруги при заданому перерізі лінії F і зрівняти знайдену величину із допустимою.

Якщо задана допустима втрата напруги виражена у відсотках до номінальної напруги U_н, то завдання вибору необхідного перерізу проводу можна розв'язати за допомогою наступних формул, отриманих з виразів (6-5) і (6-6) підстановкою ΔU_доп* у відсотках і розв'язком їх відносно F:

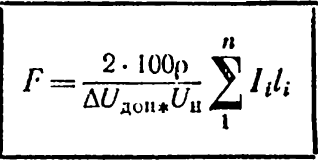(6-7)

або

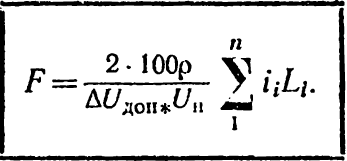(6-8)

При розрахунках буває зручно користуватися не струмами, а потужностями: нехай навантаження задані у вигляді p₁ = i₁U_н; p₂ = i₂U_н; …; p_n = i_nU_н, а потужності в лінії відповідно P₁ = I₁U_н; P₂ = I₂U_н; …; P_n = I_nU_н, тоді зазначені вище формули після підстановки i = p/U_н і I = P/U_н приймуть вид:

а) для визначення втрати напруги

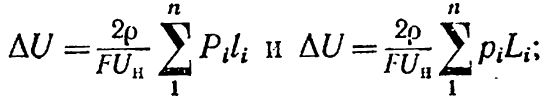(6-9)

б) для визначення перерізу проводів

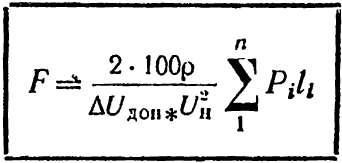і 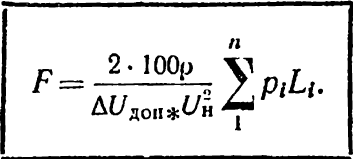(6-10)

У всіх наведених вище формулах приймають наступні розмірності: струми – А, навантаження – Вт, напруги – В, довжини – км, питомі опори Ом·мм²/км і перерізу проводів – мм². Якщо питомий опір виражений через Ом·мм²/м, то довжина повинна враховуватися в метрах.

Виведені формули для визначення втрат напруги і перерізів провідників слушні не тільки для ліній постійного струму, але і для двопровідних ліній змінного струму з активним навантаженням; тому вони мають практичне застосування, наприклад для розрахунків освітлювальних двопровідних відгалужень ліній трифазного струму.

П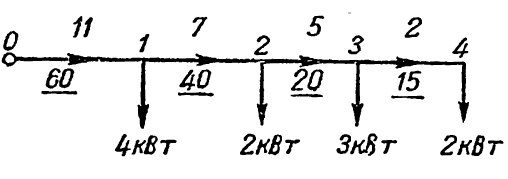 риклад 6-1. Вибрати перетин проводів освітлювальної двопровідної лінії з номінальною напругою 220 В при припустимій втраті напруги 6%. Довжини (у метрах) і навантаження (у кіловатах) зазначені на мал. 6-2. Провода - мідні, марки ВРГ.

Мал. 6-2. Схема до прикладу 6-1

Визначаємо потужності на ділянках лінії: Р₄ – 2 кВт, Р₃ = 2 + 3 = 5 кВт, Р₂ = 5 + 2 = 7 кВт і Р₁ = 4+7=11 кВт

Переріз проводу при питомому опорі міді ρ=18,0·10^-3 Ом·мм²/м визначаємо по формулі (6-10):

або

приймаємо переріз проводу ВРГ 2 х 16 мм².

Допустимий струм для цього проводу І_доп = 100 А (табл. П.2-2). Фактичний струм на першій ділянці

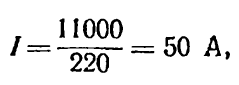
що значно менше допустимого.

6-3. Розрахунки ліній трьохфазного струму з навантаженням на кінці по втраті напруги

Р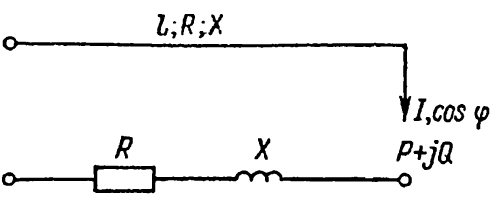 озглянемо найпростішу схему лінії трифазного струму із симетричним навантаженням на кінці (мал. 6-3). Довжина лінії l, активний опір R, індуктивне X.

Навантаження задане або струмом І і коефіцієнтом потужності соs φ при фазній напрузі U_ф на кінці лінії, або трифазною потужністю в комплексному вигляді:

Мал. 6-3. Схема заміщення лінії

трьохфазного струму з навантаженням на кінці

де – активна потужність навантаження; – реактивна потужність; U – лінійна напруга

Повна потужність

і

Тут і далі при зображенні потужності в комплексному виді S=P+jQ, будемо приймати, що знак плюс в уявній частині виразу характеризує споживання реактивної індуктивної потужності електроприймачів (відстаюча реактивна потужність навантаження). Позитивний знак в активних і реактивних складових повної потужності символізують їхній однаковий напрямок від генератора до споживача. Підстановка в цей вираз реактивної потужності зі знаком мінус (S=P–jQ) буде означати напрямок реактивної потужності, зворотній стосовно напрямку активної складової повної потужності, що відповідає споживанню електроприймачів ємнісної реактив­ної потужності (випереджальна реактивна потужність навантаження) або, що те ж, видачі їм реактивної індуктивної потужності в мережу.

Розрахунок лінії почнемо з розгляду векторної діаграми струмів і напруг (мал. 6-4) для однієї фази лінії, що допустимо, так як навантаження в усіх фазах симетричне. Припустимо, що струм навантаження І, соs φ і напруга U_Ф наприкінці лінії відомі, а необхідно визначити напругу U'_Ф і соs φ' на початку лінії. По позитивному напряму речовинної осі системи координат орієнтуємо вектор заданої напруги на кінці лінії U_Ф (0А); тоді вектор струму I буде перебувати в іншому квадранті під заданим кутом φ до напруги в бік відставання, що відповідає індуктивному навантаженню споживача. При зображенні струму в комплексному вигляді його складова І_а (активна) направлена по осі речовинних значень у позитивному напрямку, а складова – jI_r (реактивна) по осі уявних значень у негативному направленні, тобто:

Т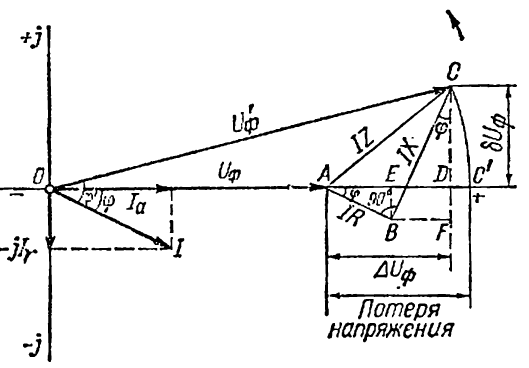 аким чином при прийнятому розташуванні вектора напруги і струму на векторній діаграмі знак мінус в уявній частині комплексу струму характеризує індуктивний (відстаючий) струм навантаження електроприймача.

Для ємнісного струму навантаження (випереджального) уявна частина його повинна бути спрямована по позитивному напрямку осі уявних значень і в цьому випадку їй присвоюється знак плюс (+jI_r).

Мал. 6-4. Векторна діаграма лінії з

навантаженням на кінці

Значення складових струму , очевидно, рівні:

Щоб визначити напругу на початку лінії, треба від кінця вектора U_Ф відкласти паралельно вектору струму I вектор падіння напруги в активному опорі лінії IR і під кутом 90° до нього в бік випередження - вектор спадання напруги в реактивному опорі IX (див. трикутник АВС на мал. 6-4). З'єднавши отриману точку С з початком координат О, одержимо шуканий вектор фазної напруги на початку лінії 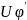U'_Ф орієнтований стосовно струму під кутом φ'.

Вектор AC, чисельно рівний

являє собою величину повного спадання напруги в одній фазі розглянутої лінії. Спадання напруги в лінії може бути розкладене на складові:

а) поздовжню ΔU_ф = AD (спрямовану вздовж вектора U_ф);

б) поперечну δU_ф = DС, тобто

Визначимо ці складові. Для цього спроектуємо вектори АВ = IR і ВС = IX на напрямки речовинної і уявної осей, у результаті чого (див. мал. 6-4) одержимо наступні відрізки:

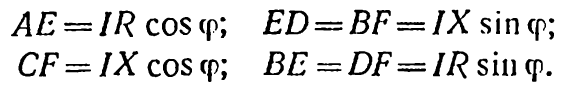
Звідси поздовжня складова

(6-11)

поперечна складова:

(6-12) отже, напруга на початку лінії буде:

а модуль напруги:

(6-13)

При розрахунках мереж місцевого значення звичайно вводять спрощення, яке полягає у тому, що напруги на початку лінії визначають не по спаданню напруги, а по втраті напруги.

Як уже вказувалося в § 6-1, під втратою напруги розуміють алгебраїчну різницю абсолютних значень напруг на початку і в кінці лінії, тобто U' – U. Практично вона може бути отримана як різниця показань вольтметрів, включених на початку і в кінці лінії. Не потрібно це поняття змішувати з поняттям спадання напруги, що є геометричною різницею потенціалів між цими точками.

Для визначення втрати напруги на діаграмі засікаємо вектором ОС відрізок ОС' на речовій осі. Очевидно, що відрізок

і буде являти собою втрату напруги. Але тому що для місцевих мереж кути між U'_ф і U_ф досить малі, а отже, досить малий і відрізок DС, то з достатньою точністю можна вважати, що втрата напруги приблизно дорівнює поздовжній складовій падіння, напруги, тобто

(6-14)

Помилка від прийнятого допущення в найгіршому випадку, коли соs φ – 1, не перевищує 0,55%, а при соs φ < 1 має ще менше значення.

Таким чином, розрахунок мереж на втрату напруги зводиться до визначення поздовжньої складової спадання напруги по формулі (6-11).

Втрату лінійної напруги визначають по формулі:

(6-15)

причому векторна діаграма лінійних напруг буде виглядати аналогічно діаграмі фазних напруг (мал. 6-4).

При розрахунках мереж на втрату напруги користування формулами (6-14) і (6-15) викликає деякі труднощі, тому що доводиться визначати струми навантаження, соs φ і sin φ у лініях. Тому частіше воліють користуватися в якості вихідних даних значеннями потужності, вираженої в комплексній формі:

Так як:

(де U — напруга наприкінці лінії), то, підставивши ці вираження у формулу (6-15), втрату напруги визначимо у вигляді:

або

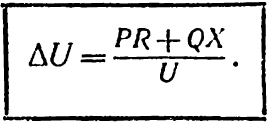(6-16)

При розрахунках часто напруга в приймачів буває невідомою, тому з достатньою точністю у формулі (6-16) замість дійсної напруги U наприкінці лінії можна приймати номінальну напругу мережі U_н; тоді:

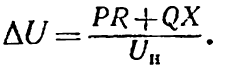(6-17)

Так як для однорідних ліній при r₀/x₀ = const; R = r_ol, a X=x₀l [див. формули (3-1) і (3-9)], то вираз (6-17) можна переписати в такий спосіб:

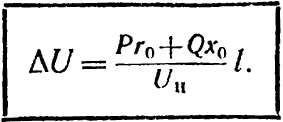(6-18)

У виведених формулах для одержання ΔU у вольтах величину Р підставляють у ватах або кіловатах, Q - у вольт-амперах реактивних або кіловольт-амперах реактивних, і тоді напруга повинна бути підставлена у вольтах або кіловольтах відповідно. Опори приймаються в омах.

Для визначення втрати напруги у відсотках користуються формулою:

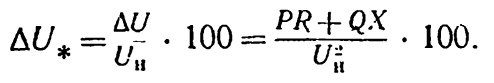(6-19)

У цьому випадку розмірність величин, що входять у формулу, повинна бути прийнята такою: (Вт·Ом + вар·Ом)/В².

Завдання на СРС:

1. Повторити по конспекту матеріал лекції.

2. Самостійно вивчити та до наступної лекції законспектувати матеріал цієї лекції по [6] с.25-36.

Література: [6] с.25-36; [7] с.9-19 (в тому числі і на СРС).

§ 4.2. Втрати і падіння напруги. Розрахунки режимів за даними кінця(почала) передачі

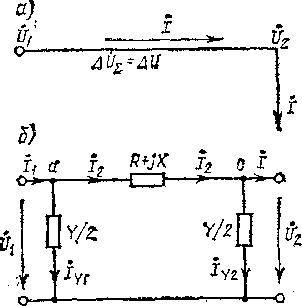
Якщо відомі початкові ці лінії, наприклад кінця передачі, тобто задані струм I і напруга у споживача (рис. 4.2.1, а), то, щоб визначити напругу на живлячому кінці, потрібно до напруги додати падіння напруги , викликане струмом (потужністю), - що протікає по лінії,

(4.2.1)

Цей вираз справедливий як для фазної, так і для лінійної напруги.

Визначимо величину при одного або декількох навантажень. Для цього замінимо дану лінію П-образною симетричною схемою заміщення(рис. 4.2.1, б) з опорами R і X і провідністю . Тоді струми поперечних провідностей

Рис. 4.2.1. Лінія електропередачі

і схема її заміщення

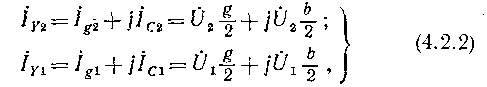
а струми в лінії

(4.2.3)

Зневага поперечною провідністю. Зазвичай для місцевих мереж струмами поперечної провідності нехтують, тобто вважають, що . У тих випадках, коли поперечною провідністю нехтувати не можна, лінію (трансформатор) замінюють чотириполюсниками з постійними АВС і D, що розглядається далі в данному параграфі. Методи знаходження узагальнених постійних вивчаються в ТОЕ.

Подовжня і поперечна складова падіння напруга. Втрата напруги. Направимо вектор по речовій осі (рис. 4.2.2). Невідомий вектор зображуватимемо умовно, як показано на малюнку. Тоді згідно (4.2.1) відрізок рівний

(4.2.4)

Ця геометрична різниця напруги на початку і кінці лінії називається падінням напруги.

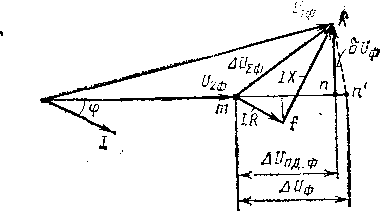
Рис. 4.2.2. Векторна діаграма струму і напруги ліній

Якщо від кінця вектору (від точки к) зробити циркулем зарубку на речовій осі (див. точку n'), то отримаємо відрізок mn', рівний

(4.2.5)

Ця різниця алгебри напруги на початку і кінці лінії називається втратою напруги.

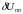Вектор падіння напруги може бути розкладений на дві складових. Проекція цього вектору на речову вісь (відрізок mn) називається подовжньою складовою падіння напруги , а проекція на уявну вісь (відрізок kn) - поперечній складовой падіння напруги . Таким чином,

(4.2.6)

Знаючи величини по заданій напрузі можна знайти абсолютне значення напруги на початку лінії:

(4.2.7)

По векторній діаграмі струму і фазної напруги лінії (рис. 4.2.2) складемо вирази для визначення подовжньою і поперечною що становлять падіння напруги і знайдемо значення по заданих . Проектуємо вектори IR і IX трикутника падіння напруги mfk на речову вісь. Отримуємо подовжню складову падіння напруги

(4.2.8)

Аналогічно проектуємо ці ж вектори на уявну вісь. Отримуємо поперечну складову падіння напруги

(4.2.9)

У (4.2.8) і (4.2.9) замінюємо значення через потужності

(4.2.10)

Отримуємо

Замінюємо фазні складові лінійними, тобто множимо на . Тоді

При точних розрахунках напруга повинна відповідати напрузі в точці, до якої прикладена потужність. Проте у ряді випадків, коли напруга у приймачів невідома, розрахунок можна проводити з достатньою точністю по номінальній напрузі , а не по фактичному.

Другий член під коренем в (4.2.7) значно менше першого. Тому впливом поперечної складової можна нехтувати, оскільки ця складова часто мало міняє абсолютне значення , тобто відрізок на рис. 4.2.2 у більшості випадків можна не враховувати. Вираження (4.2.7) набуває вигляду

(4.2.13)

тобто

Таким чином, втрату напруги можна прирівняти подовжній складовій падіння напруги. Отже,

При декількох навантаженнях втрата напруги

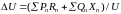(4.2.14)

або

(4.2.15)

Розрахунок по (4.2.15) може проводитися або по потужностях (чи по струмах) навантажень 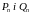або по лінійних потужностях . Відповідно плечі для цих навантажень будуть різними. У першому випадку плечима є повні опори від кожного навантаження до живлячого пункту, в другому - опір тільки того

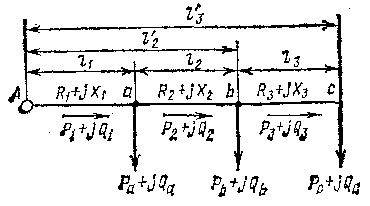
Рис. 4.2.3. Схема лінії з трьома навантаженнями

ділянки, по якій протікає ця лінійна потужність (струм). На рис. 4.2.3 показана лінія з трьома навантаженнями.

При розрахунку по потужностях навантажень

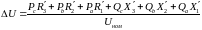(4.2.16)

Як видно з рис.

І відповідно

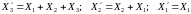
При розрахунку по лінійним потужностям

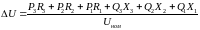(4.2.16a)

При однаковому перерізі ліній і розташуванні дротів по усій довжині . Питомі опори можуть бути винесені за знак суми, тоді розрахунок проводиться по д довжтнам, що дуже зручно при практичних розрахунках.

При розрахунку по потужностях навантажень

При розрахунку по лінійних потужностях

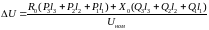
Очевидно, що

Розрахунок обома методами дає один і той же результат, якщо втратами потужності на першому етапі розрахунку нехтувати.

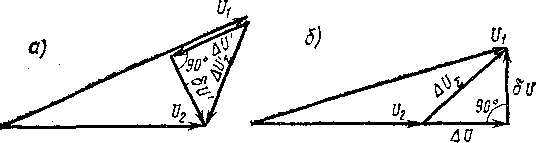
Рис. 4.2.5. Векторні діаграми напруги лінії

При багатьох навантаженнях все робиться аналогічно. Починаючи від кінця вектору заданої напруги у кінці лінії переходять послідовно від навантаження до навантаження до напруги на початку лінії. Якщо відома, наприклад, напруга початку передачі і вимагається визначити напругу кінця передачі (рис. 4.2.5, а) то абсолютне значення напруги у кінці передачі, аналогічно (4.2.7), набуде вигляду

(4.2.17)

Як видно з (4.2.17), в протилежність (4.2.7) величина віднімається з величини . Якщо відома напруга кінця передачі , то векторна діаграма відповідає рис. 4.2.5, б. Потрібно мати на увазі також, що при визначенні значень напруги кінця або початку передачі .

Визначення режиму напруги. У більшості випадків заданою є напруга передавальних кінців . Тому розрахунок виконується по (4.2.17) від передавального кінця мережі до її приймального кінця.

Щоб знайти напругу по заданому необхідно:

1) шляхом поступового переміщення по кожній з гілок схеми (від попередньої до подальшого навантаження) визначити падіння (4.2.11) і (4.2.12) або втрати по (4.2.14) напругу;

2) віднімаючи ці знайдені втрати (падіння) напруги зі значень напруги найближчого передавального кінця кожної гілки, знайти напругу кінцевого вузла даної гілки, який для подальшого розрахунку буде являтися вже передавальним кінцем наступної гілки і т. д.

У мережах 110 кВ і нижче вплив поперечної складової часто не враховується, оскільки воно порівняльне мало впливає на результат виразів (4.2.7), (4.2.17).

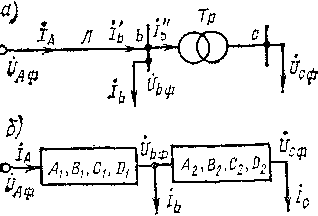Розрахунок лінії передачі з використанням чотириполюсників(з урахуванням поперечної провідності). У складних мережах, де потрібний облік поперечної провідності, усі елементи мережі замінюються чотириполюсниками і розрахунок усіх струмів і напруги проводиться з урахуванням параметрів цих чотириполюсників. Наприклад, якщо потрібно розрахувати

Рис, 4.2.6. Схема електропередачі з урахуванням

поперечної провідності і чотириполюсники,

замінюючі елементи передачі

електропередачу (рис. 4.2.6, а) із заданим струмом і напругою , кожен елемент цієї передачі замінюється чотириполюсником. Лінія Л замінюється чотириполюсником з узагальненими постійними а трансформатор Тр - з (рис. 4.2.6, б). Оскільки навантаження в точці рівне , то рівняння чотириполюсників будуть

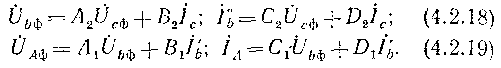
За допомогою чотириполюсників розрахунок зручніше проводити для однієї фази лінії, тобто у рівняння підставляються фазні значення напруги.

Таким чином, пересуваючись від кінця передачі до початку по заданих , можна знайти по рівняннях (4.2.18) в точці . Аналогічно по (4.2,19), знаючи , визначаються на початку лінії.

Якщо проміжних навантажень немає ( ), то можна знайти струм і напруга на початку передачі по заданих значеннях у кінці (рис. 4.2.7, а), склавши при цьому послідовно обидва чотириполюсники для лінії і трансформатора (рис. 4.2.7, б). Розрахунок в цьому випадку проводиться по еквівалентному чотириполюснику з узагальненими постійними А, В, С і D (рис. 4.2.7, в).

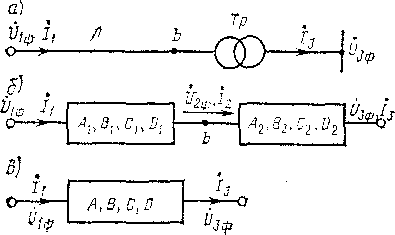
Рис. 4.2.7. Схема послідовного складання чотириполюсників

Послідовне складання чотириполюсників. Щоб знайти еквівалентний чотириполюсник, необхідно визначити узагальнені постійні А, В, С і D. Складаємо рівняння чотириполюсників аналогічно (4.2.18) і (4.2.19) при заданих .

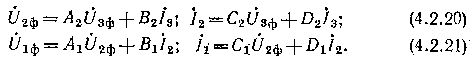
У рівняннях (4.2.20) і (4.2.21) чотири невідомих 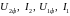. Вирішуючи спільно ці рівняння, виразимо через і з новими постійними А, B, C і D еквівалентного чотириполюсника. Тоді остаточно

де

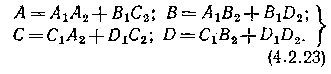
Рис. 4.2.8. Схема паралельного

складання чотирьохполюсників

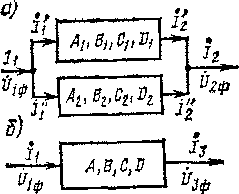
Паралельне складання чотириполюсників (рис. 4.2.8, а). Паралельне складання чотириполюсників відрізняється від послідовного тим, що невідомих не чотири, а шість, оскільки струми на вході і виході розгалужуються. Невідомі результуючого чотириполюсника (рис. 4.2.8, б) знаходяться по шести рівняннях:

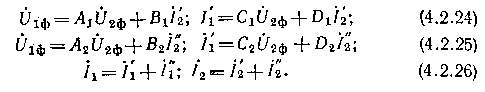
Вирішивши спільно ці рівняння, остаточно отримаємо рівняння для еквівалентного чотириполюсника:

де

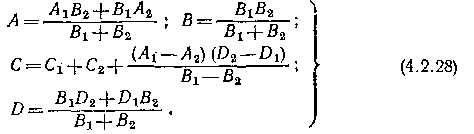
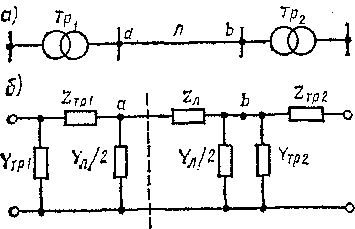Скорочення числа чотириполюсників. Кожен елемент передачі (лінія, трансформатор) повинен замінюватися своїм чотириполюсником. Проте для спрощення розрахунків іноді є можливість скоротити число чотириполюсників. Наприклад, на рис. 4.2.9, а показана передача трансформатор - лінія- трансформатор. Трансформатор замінюваний Г-подібною схемою заміщення; лінію- П-образної і - знову Г-подібною схемою. Здавалося б, в цьому випадку потрібно послідовно складати три чотириполюсника. Проте з аналізу схеми (рис. 4.2.9, б) видно, що симетричні чотириполюсники П- і Г-подібної можна

Рис. 4.2.9. Схема можливого скорочення

числа чотириполюсників

замінити двома несиметричними П- і Т-подібними: зліва від штрихової лінії і справа. Таким чином розрахунок проводиться вже не для трьох, а для двох чотириполюсників, при цьому заздалегідь складається паралельна провідність .
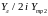