
- •§ 4. Криволінійні інтеграли першого роду (по довжині дуги) і їх застосування в задачах фізики.
- •Фізичні задачі, які приводять до обчислення криволінійного інтеграла першого роду
- •Завдання 12
- •Розділ іі. Невластиві інтеграли Рімана §1. Теоретичні питання.
- •§ 2. Означення невластивих інтегралів першого і другого роду. Збіжність невластивого інтеграла від невід’ємної функції.
- •Завдання 13
- •§ 3. Абсолютна і умовна збіжність невластивих інтегралів.
- •Завдання 14
- •Завдання 15
- •§4. Інтеграли Ейлера: гама і бета функції
- •Завдання 16
Завдання 14
Дослідити на збіжність наступні інтеграли.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Завдання 15
Дослідити на абсолютну і умовну збіжність інтеграли
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
§4. Інтеграли Ейлера: гама і бета функції
7. Гама і бета функції Ейлера.
Невластиві інтеграли


називають інтегралами Ейлера.
При
 інтеграли збігаються. Деякі наближені
значення
інтеграли збігаються. Деякі наближені
значення
 наведено
у таблиці (див. додаток).
наведено
у таблиці (див. додаток). ,
,
 .
.
Зокрема
![]()
![]()



Приклад 17.
Знайти об’єм тіла обертання, яке
утворюється при обертанні фігури,
обмеженої астроїдою
![]()
![]() навколо
осі Оу.
навколо
осі Оу.
■ Зробимо схематичний рисунок (рис. 7)

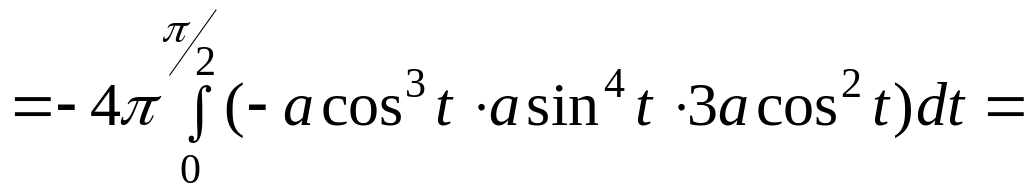
 .
.
При обчисленні інтеграла застосуємо формули:

![]() .
.
У
нашому випадку
![]() і інтеграл
і інтеграл

 .
.
Отже,
 ■
■
Приклад 18. Знайти площу фігури, обмеженої кривою
![]() .
.
■ Зауважимо,
що графік кривої симетричний відносно
осей Ох
і Оу,
отже
![]() .
Перейдемо до полярних координат:
.
Перейдемо до полярних координат:
![]()
![]() .
.
Отримуємо:
![]()
![]()
![]() .
.
Тоді
 .
.
Застосуємо формули
 ,
,
![]() ,
,
У
нашому випадку
![]()
![]() ,
тому
,
тому

![]()
 .
■
.
■
Приклад 19.
Довести, що інтеграл збігається і знайти
його наближене значення
 .
.
■. Запишемо інтеграл у вигляді
 .
.
Маємо
![]()
![]() За цих умов функція
За цих умов функція
![]() приймає скінченне значення. З іншої
сторони зауважимо, що за теоремою
порівняння
приймає скінченне значення. З іншої
сторони зауважимо, що за теоремою
порівняння
 ~
~ при
.
Для
при
.
Для
![]() невластивий інтеграл першого роду
збігається. Знайдемо наближене значення
інтеграла
невластивий інтеграл першого роду
збігається. Знайдемо наближене значення
інтеграла
 .
.
За таблицею для гама-функції (див. додаток) отримуємо:
![]() ;
;
![]() .
.
Отже
![]() .
■
.
■
Завдання 16
Довести збіжність наступних інтегралів і знайти їх наближені значення, користуючись таблицею гама–функцій.
|
|
|
|
|
|
|
|
|
|
|
|
Знайти площу фігури, обмеженої кривою
|
|
|
|
|
|
Знайти об’єм тіла, яке утворене обертанням фігури, обмеженої лінією
797.
![]() навколо осі Ох.
навколо осі Ох.
798.
![]() навколо осі Ох.
навколо осі Ох.
799.
![]() навколо осі Ох.
навколо осі Ох.
800.
![]() навколо осі Оу.
навколо осі Оу.

 .
. .
. .
.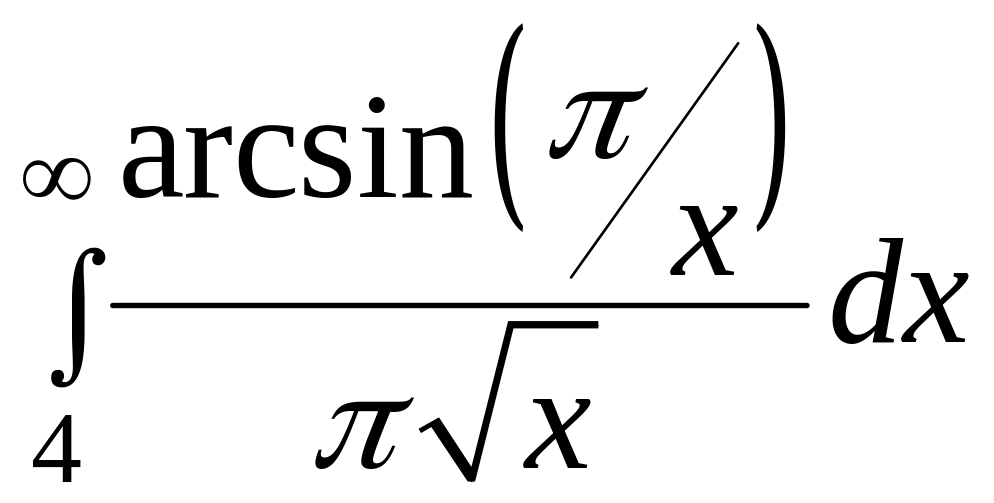 .
.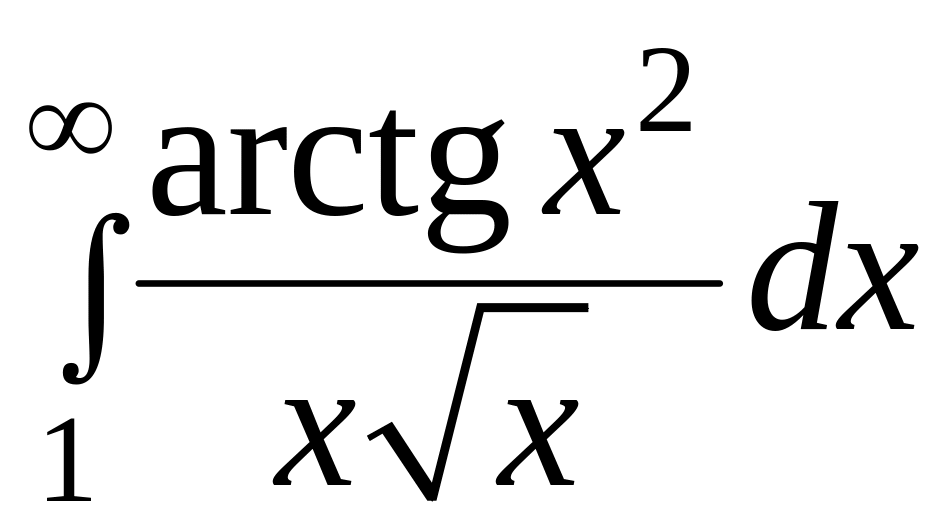 .
. .
. .
.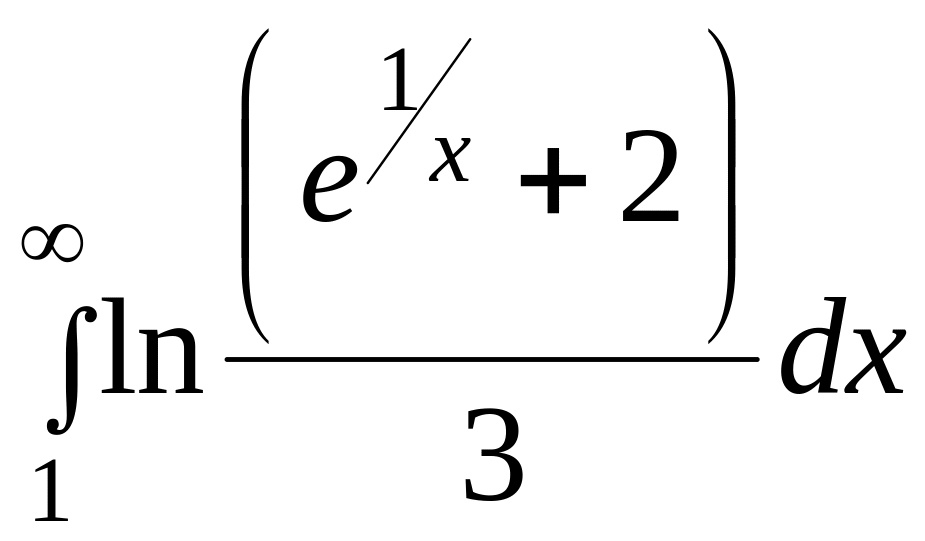 .
. .
. .
. .
. .
. .
. .
.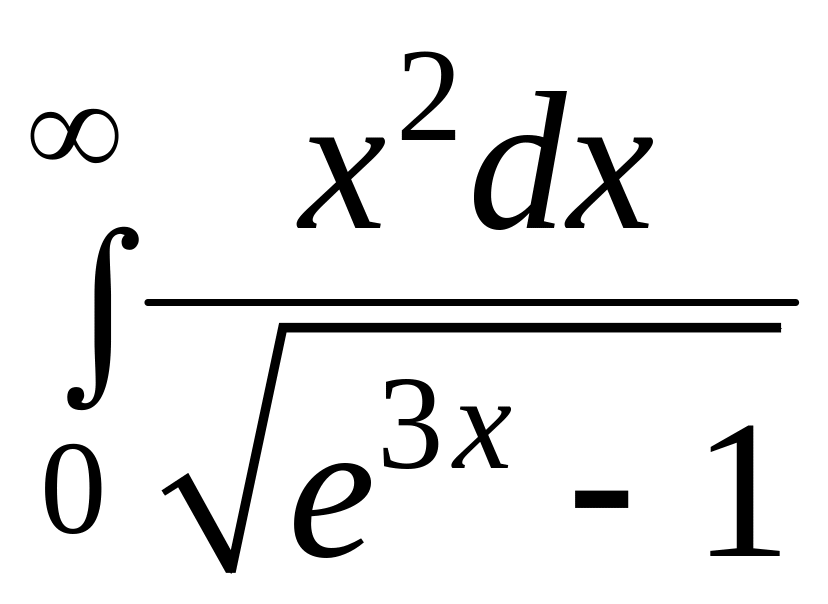 .
. .
. .
.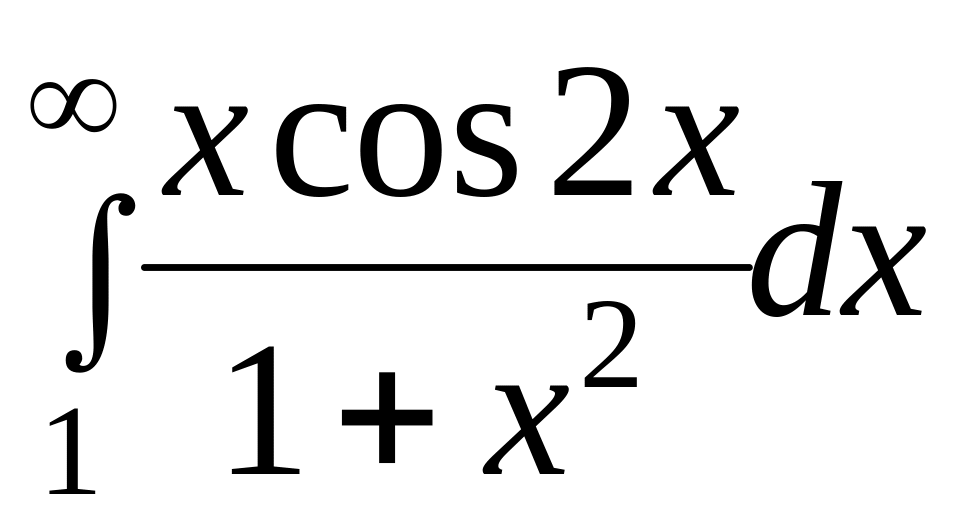 .
. .
. .
. .
. .
. .
. .
. .
.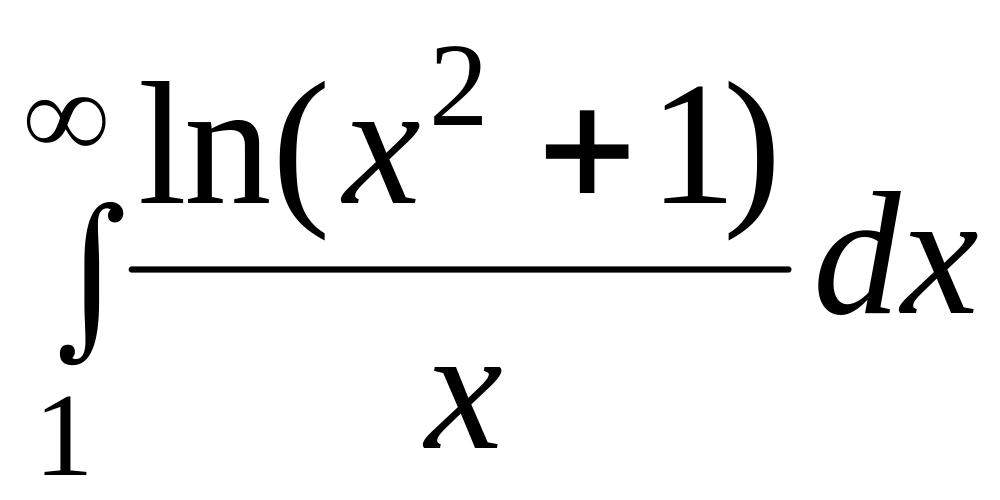 .
. .
.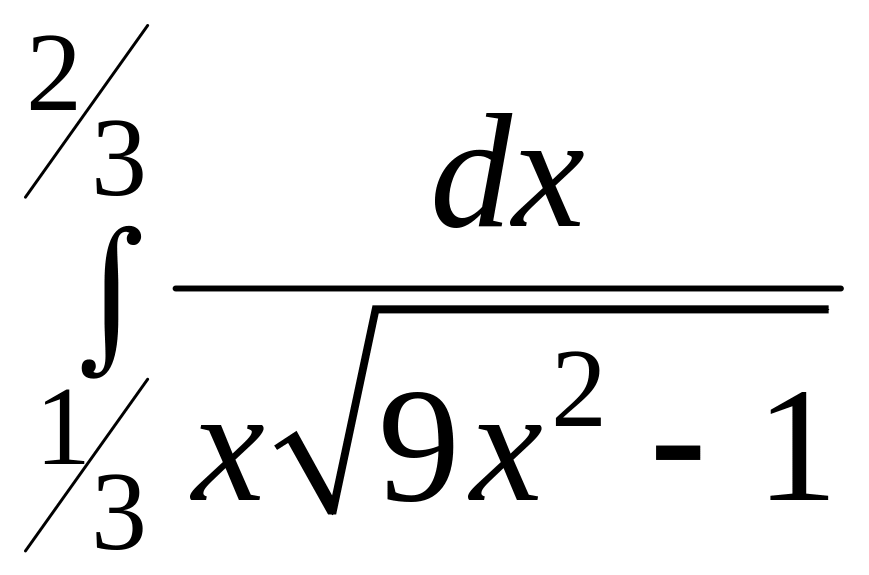 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.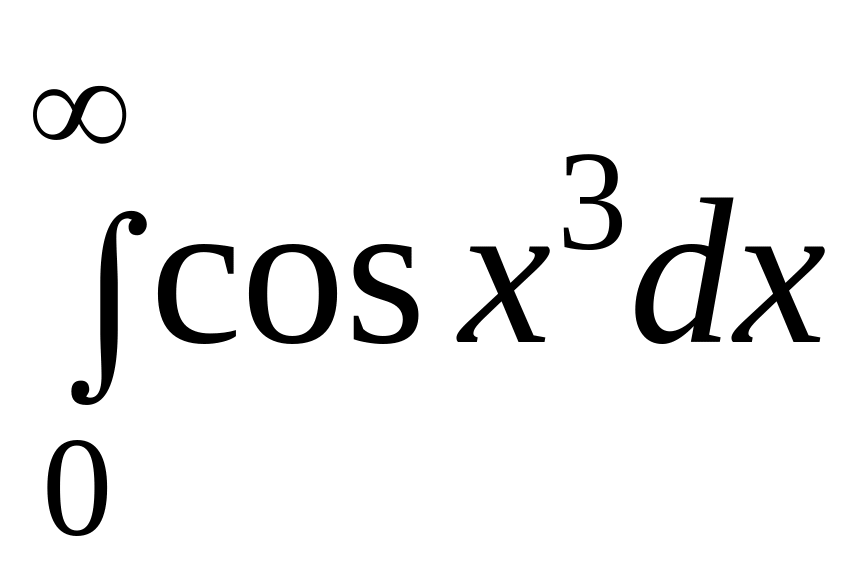 .
.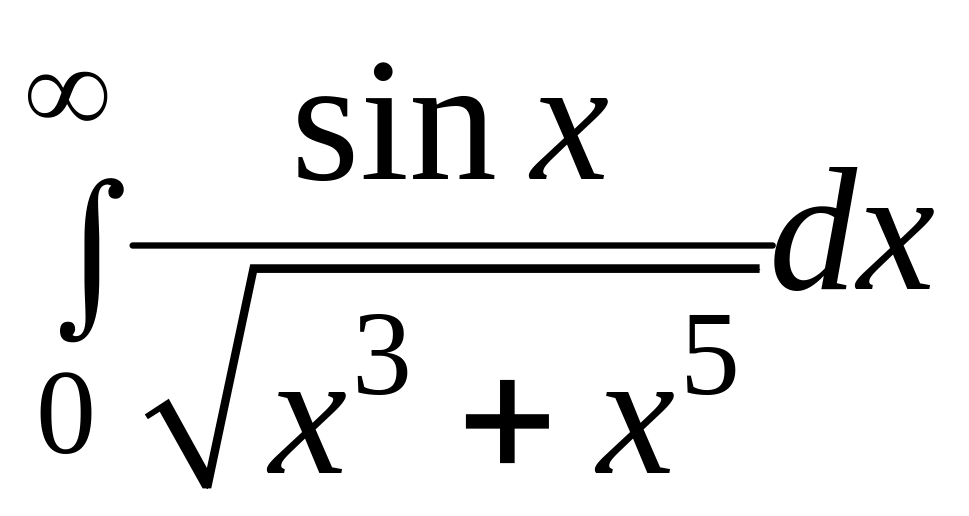 .
. .
. .
. .
. .
. .
. .
. .
. .
. .
.
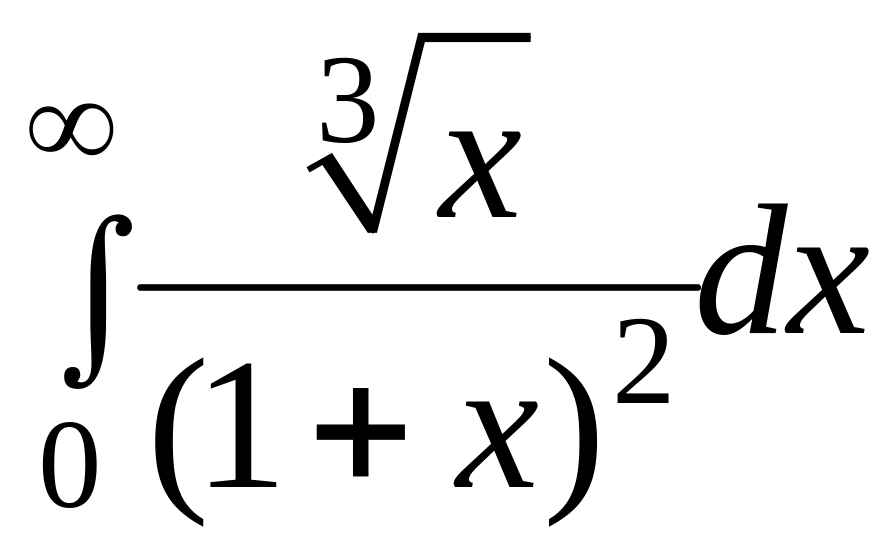 .
. .
. .
. .
.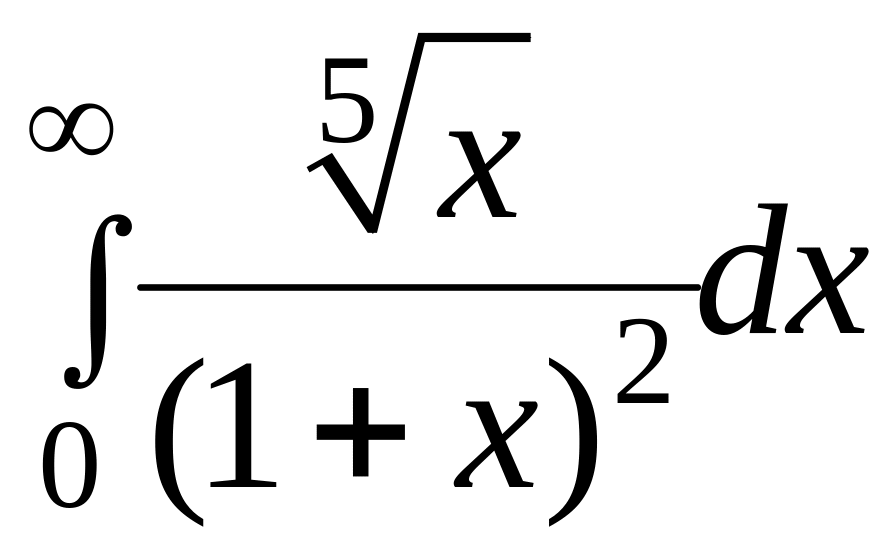 .
. .
. .
. .
. .
. .
.