
- •§ 4. Криволінійні інтеграли першого роду (по довжині дуги) і їх застосування в задачах фізики.
- •Фізичні задачі, які приводять до обчислення криволінійного інтеграла першого роду
- •Завдання 12
- •Розділ іі. Невластиві інтеграли Рімана §1. Теоретичні питання.
- •§ 2. Означення невластивих інтегралів першого і другого роду. Збіжність невластивого інтеграла від невід’ємної функції.
- •Завдання 13
- •§ 3. Абсолютна і умовна збіжність невластивих інтегралів.
- •Завдання 14
- •Завдання 15
- •§4. Інтеграли Ейлера: гама і бета функції
- •Завдання 16
§ 4. Криволінійні інтеграли першого роду (по довжині дуги) і їх застосування в задачах фізики.
Означення
(гладкої дуги). Для простоти розглянемо
плоску криву (дугу) Г,
яку описує векторна функція
![]() .
Побудуємо поділ
.
Побудуємо поділ
 .
.
Кожному значенню
параметра
![]() відповідає точка
відповідає точка
![]() .
Знайдемо довжину ламаної, вписаної в
Г:
.
Знайдемо довжину ламаної, вписаної в
Г:
![]() .
.
Довжиною дуги
Г
називають
![]() ,
якщо
,
якщо![]() ,
тоді Г
називають спрямлюваною,
а
,
тоді Г
називають спрямлюваною,
а
![]() –
її довжиною.
–
її довжиною.
Дугу
Г називають
гладкою,
якщо
![]() і
і
![]() для
для
![]() .
.
Теорема 1:
гладка дуга спрямлюється і
 ,
де
,
де
 ;
;для гладкої незамкненої дуги
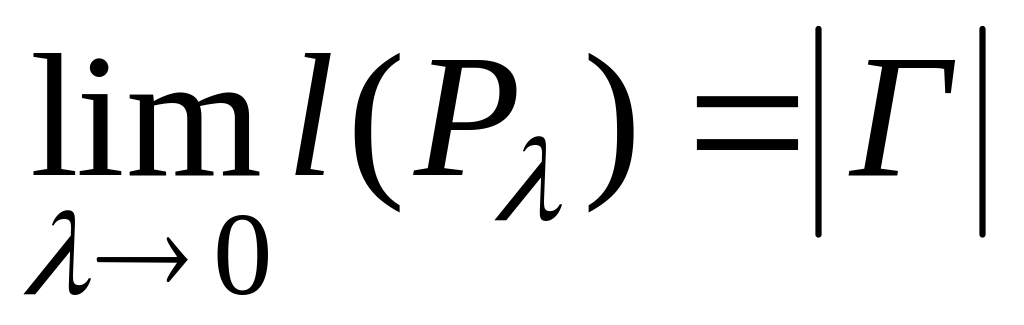 ;
;довжина гладкої дуги в малому еквівалентна довжині хорди, що її стягує.
Означення
(параметризація гладкої дуги). Для
гладкої дуги Г
введемо новий параметр
![]() – довжина дуги від точки А
(
– довжина дуги від точки А
(![]() )
до змінної точки М(t)
(
),
)
до змінної точки М(t)
(
),
![]() – строго монотонно зростає на
– строго монотонно зростає на
![]() :
:
![]() ,
,
![]() і
і
![]() .
Параметр
.
Параметр
![]() називають натуральним
параметром.
називають натуральним
параметром.
Означення
(криволінійного інтеграла першого
роду).Розглянемо гладку криву Г:
![]() ,
,
![]() для
.
Введемо натуральний параметр
для
.
Введемо натуральний параметр
![]() і побудуємо поділ
і побудуємо поділ
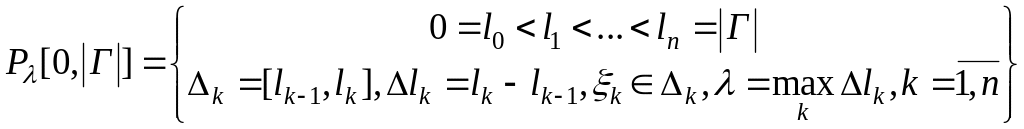 .
.
Кожному значенню
параметра l
на дузі Г
відповідає точка. Позначимо через
![]() точку, яка відповідає значенню параметра
точку, яка відповідає значенню параметра
![]() .
.
Нехай на Г
задано функцію
![]() .
Побудуємо інтегральну суму
.
Побудуємо інтегральну суму
![]() .
Якщо існує
.
Якщо існує
![]() і не залежить від поділу
і не залежить від поділу
![]() ,
вибору точки
і вибору прямування
,
вибору точки
і вибору прямування
![]() ,
тоді цю границю називають криволінійним
інтегралом першого роду (по довжині
дуги) і
позначають
,
тоді цю границю називають криволінійним
інтегралом першого роду (по довжині
дуги) і
позначають
![]() .
.
Формули обчислення криволінійного інтеграла першого роду
Г задано параметрично: , для , на Г задано функцію
 ,
тоді
,
тоді
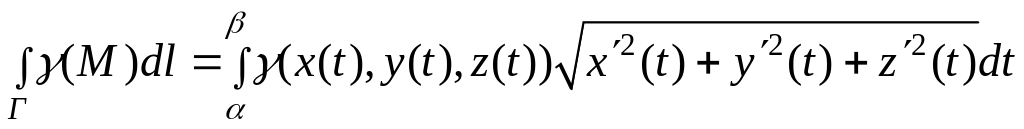 (1)
(1)
(У випадку плоскої кривої координата z відсутня (z = 0)).
Г задано явно:
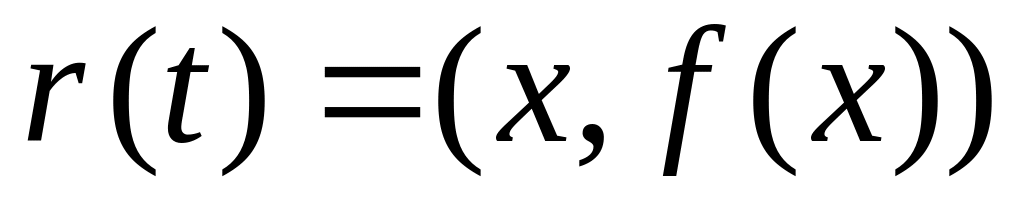 або
або
 –
плоска крива. За умов
–
плоска крива. За умов
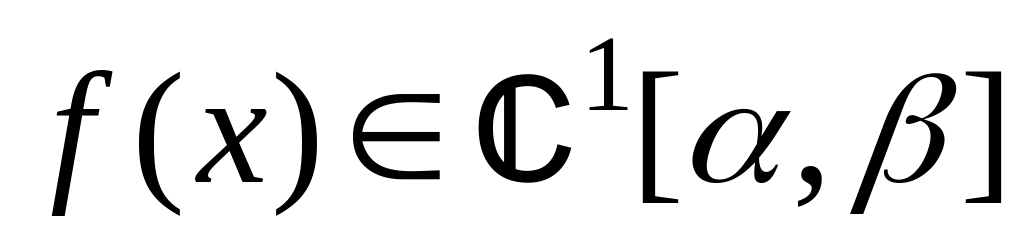 ,
,
 ,
тоді
,
тоді
 (2)
(2)
Г – плоска крива, яку задано у полярній системі координат,
![]() ;
;
![]()
![]() ,
тоді
,
тоді
 (3)
(3)
Фізичні задачі, які приводять до обчислення криволінійного інтеграла першого роду
Задача 1. Маса дуги (заряд розподілений вздовж Г)
![]() , (4)
, (4)
де
![]() –
густина маси (густина заряду:
–
густина маси (густина заряду:
![]() або
або
![]() ),
яку задано у кожній точці
),
яку задано у кожній точці
![]() .
.
Задача
2.
Центр ваги плоскої дуги:
![]()
![]() ,
,
![]() , (5)
, (5)
де
![]() – масса дуги
– масса дуги
![]() ,
,
![]() –
густина маси у точці
(якщо дуга однорідна, то вважають, що
–
густина маси у точці
(якщо дуга однорідна, то вважають, що
![]() ,
тоді
,
тоді
![]() ).
).
Теореми Гульдіна:
1.
![]() .
.
2.
 ,
де
– центр мас дуги Г,
–
масса дуги
.
,
де
– центр мас дуги Г,
–
масса дуги
.
Задача 3. Для плоскої фігури
![]() статичні моменти
відносно осей Ох
і Оу
відповідно
статичні моменти
відносно осей Ох
і Оу
відповідно
 ,
,
 (6)
(6)
Задача 4. Для плоскої гладкої дуги Г статичні моменти відносно осей Ох і Оу відповідно
![]() ,
,
![]() (7),
(7),
моменти інерції відповідно осей Ох і Оу
![]() ,
,
![]() (8)
(8)
Задача 5. Центр ваги плоскої фігури (див. задачу 3)
![]() ,
,
![]() ,
де S –
площа фігури (9)
,
де S –
площа фігури (9)
Завдання 12
Знайти масу (заряд),
розподілену вздовж дуги Г, якщо задана
густина розподілу маси (заряду)
![]() ,
,
Г – відрізок прямої
 між
точками А(0,0)
та В(1,1),
між
точками А(0,0)
та В(1,1),
 .
.Г – верхня половина кола
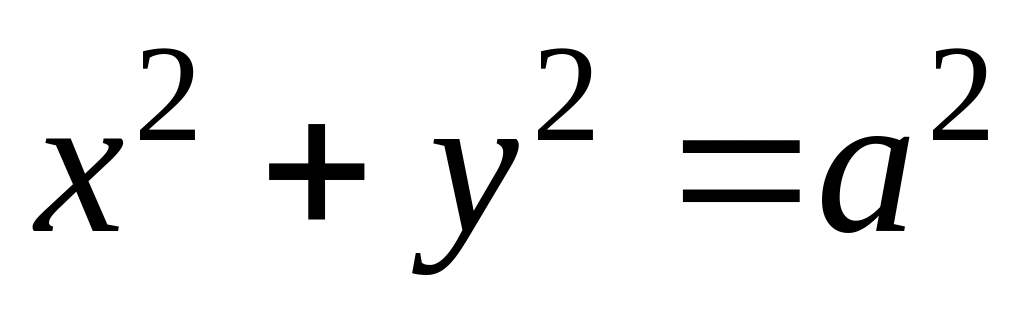 між точками А(а,0)
та В(–а,0),
між точками А(а,0)
та В(–а,0),
 ,
,
 .
.Г – дуга параболи
 між точками А(0,0)
та В(4,
між точками А(0,0)
та В(4, ),
),
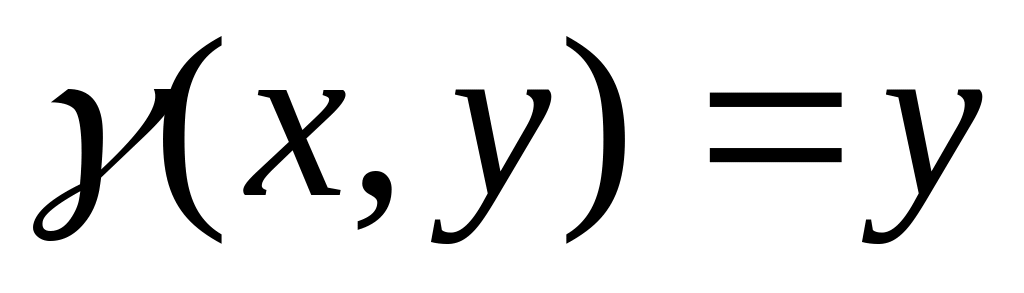 .
.Г – перша арка циклоїди
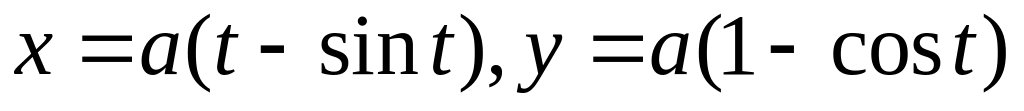 ,
,
,
,
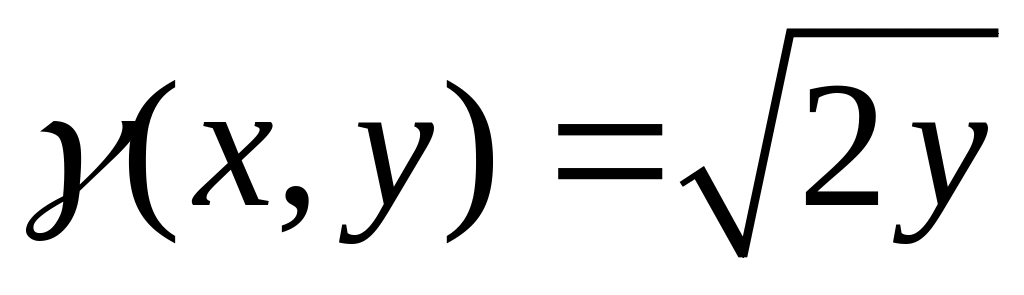 .
.Г – дуга кривої
 між точками, які відповідають
між точками, які відповідають
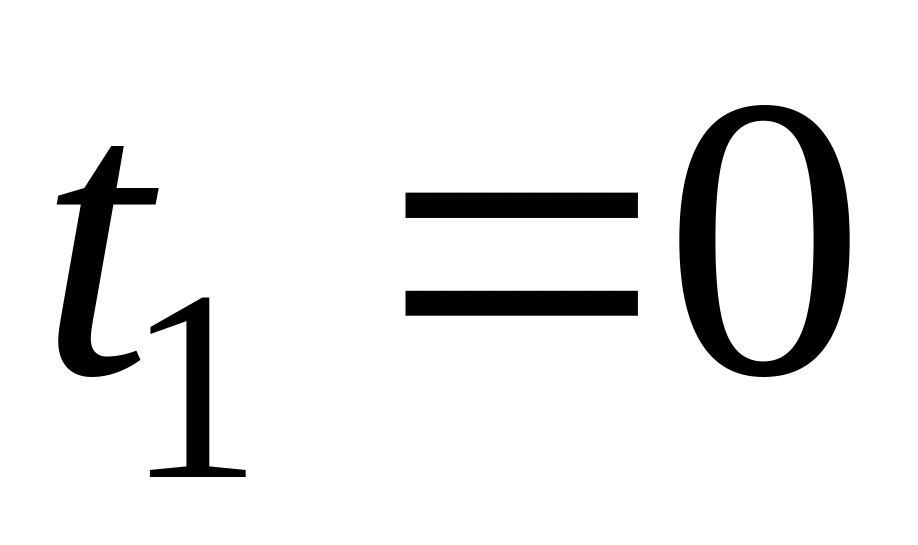 ,
,
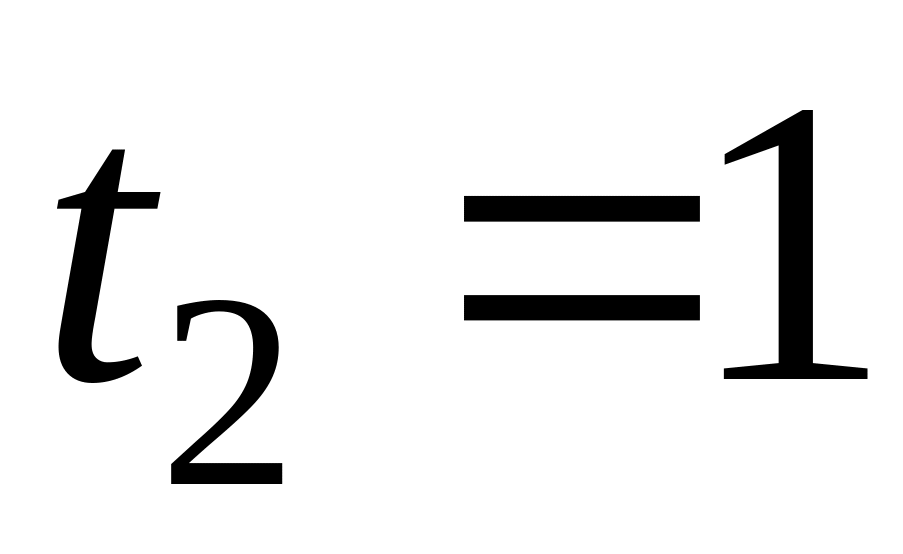 ,
,
 .
.Г – відрізок прямої
 між точками А(0,–2
) та В(4,0),
між точками А(0,–2
) та В(4,0),
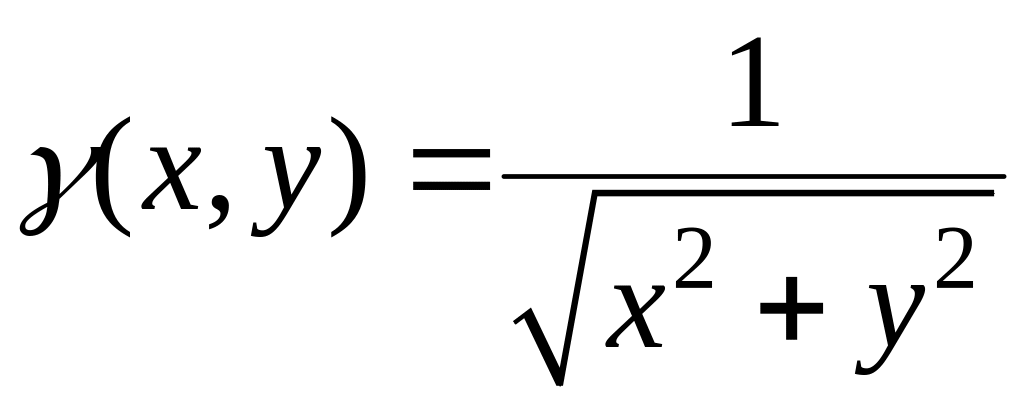 .
.Г – контур прямокутника зі сторонами, які утворені прямими
 ,
,
 .
.Г – контур трикутника з вершинами у точках О(0,0), А(1,0) та В(0,1),
 .
.Г – дуга гіперболічної спіралі
 від
точки А(
від
точки А(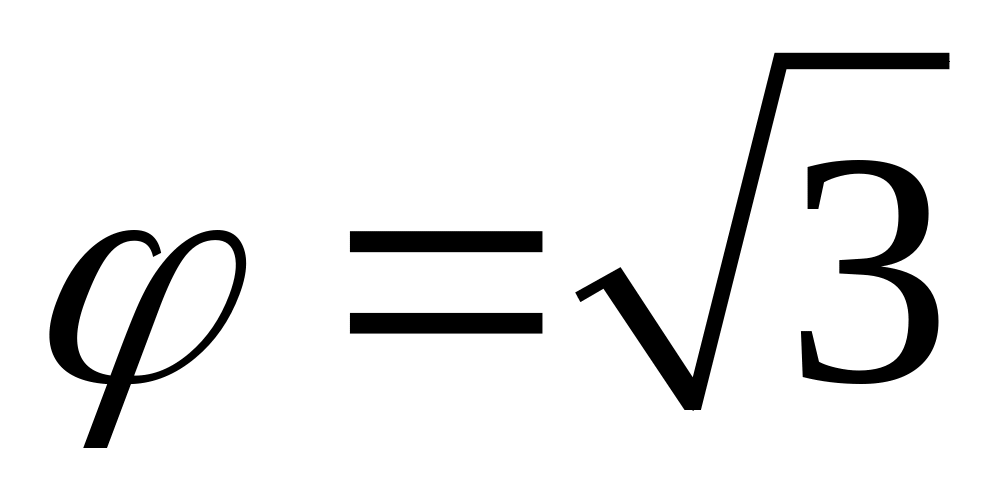 )
до В(
)
до В( ),
),
 .
.Г – дуга циклоїди , між точками А(
 )
та В(
)
та В( ),
.
),
.Г – дуга кривої
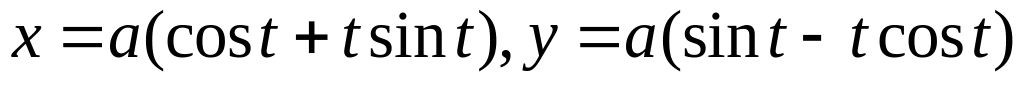 ,
між точками А(
)
та В(
),
,
між точками А(
)
та В(
),
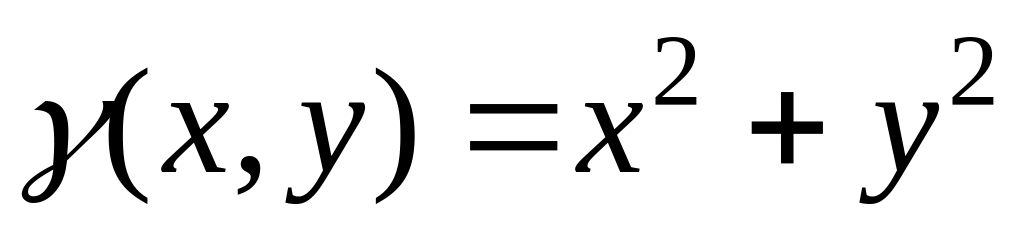 .
.Г – дуга логарифмічної спіралі
 ,
,
 ,
яка лежить всередині кола
,
яка лежить всередині кола
 ,
.
,
.Г – дуга кривої
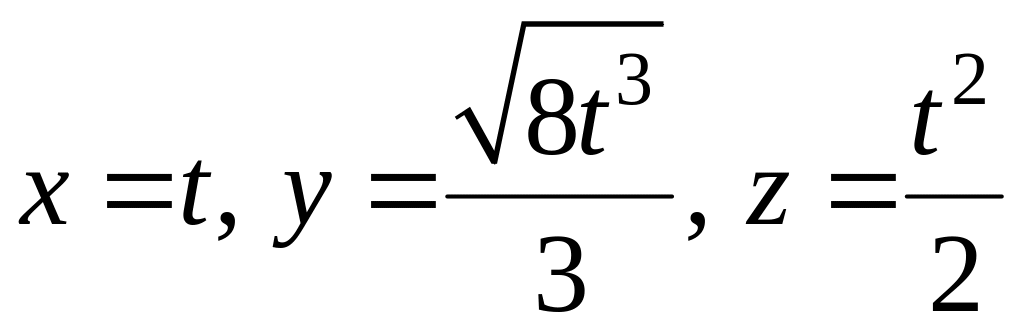 між точками А(
)
та В(
між точками А(
)
та В( ),
),
 .
.Г – дуга спіралі
 ,
, між точками А(
)
та В(
),
між точками А(
)
та В(
),
 .
.Г – коло
 ,
,
,
,

Г – коло, що є перетином поверхонь
 ,
,
,
,
 ,
,
 .
.
Знайти координати центра мас
277.
однорідної дуги циклоїди
,
![]() ;
;
278.
однорідного півкола
![]() ;
;
279.
однорідної дуги ланцюгової лінії
![]() ,
,
![]() ;
;
280.
однорідної дуги астроїди
![]() ,
,
що лежить вище осі Ох.
,
,
що лежить вище осі Ох.
Знайти статичний момент
281.
верхньої частини еліпса
 ,
,
![]() ,
відносно осі Ох;
,
відносно осі Ох;
282.
дуги параболи
,
![]() ,
відносно осі Ох;
,
відносно осі Ох;
283. дуги параболи , , відносно осі Оy;
284.
дуги кривої
![]() ,
,
![]() ,
відносно осі Ох;
,
відносно осі Ох;
285.
фігури, обмеженої лініями
![]() ,
відносно осі Ох;
,
відносно осі Ох;
Знайти момент інерції
286.
дуги кола
![]() ,
,
![]() ,
відносно осі Оy;
,
відносно осі Оy;
287.
дуги ланцюгової лінії
![]() ,
,
![]() ,
відносно осі Ох;
,
відносно осі Ох;
288. дуги ланцюгової лінії , , відносно осі Оy;
289. користуючись теоремою Гульдіна, знайти центр мас дуги астроїди , ;
290. користуючись теоремою Гульдіна, знайти центр мас фігури, обмеженої віссю Ох і однією аркою циклоїди , .
