- •1. Краткие теоретические сведения
- •1.1. Операции сравнения и логические операции
- •1.1.1. Операции сравнения
- •1.1.2. Логические операции
- •1.1.3. Логические выражения
- •1.2. Приоритет операций
- •1.3. Разветвляющийся вычислительный процесс
- •1.5. Оператор перехода
- •1.6. Пустой оператор
- •1.7.1. Короткая форма условного оператора
- •1.7.2. Полная форма условного оператора
- •1.9. Понятие составного оператора (группы операторов)
- •1.10.1. Проверка двух или более условий
- •1.10.5. Обработка нескольких условий
- •1.10.6. Вложенный условный оператор
- •1.11. Рекомендации по заданию исходных значений переменным
- •1.11.1. Операторы присваивания
- •1.11.2. Операторы ввода
- •1.11.3. Инициализация переменных
- •1.11.4. Именованные константы
- •1.12. Оператор множественного выбора switch
- •1.13. Использование отступов для улучшения удобочитаемости вашей программы
- •2. Задание
- •2.4. Задания для выполнения на занятиях
- •2.4.1. Задание 1
- •2.4.1.1. Условие задания
- •2.4.2. Задание 2
- •2.4.3. Задание 3
- •2.4.4. Задание 4
- •2.5. Задания для выполнения дома
- •2.5.1. Задание 1
- •2.5.2. Задание 2
- •3.6. Пример программы
- •3.7. Типичные ошибки при выполнении работы
- •2.5.3. Задание 3
- •3. Выводы
- •4. Требование к отчету
- •4. Краткие теоретические сведения.
- •5. Вопросы для самоконтроля
- •Литература
- •1. Краткие теоретические сведения 2
- •1.1. Операции сравнения и логические операции 2
- •1.1.1. Операции сравнения 2
1.10.6. Вложенный условный оператор
Напомним, что оператор if в полной форме называется оператором if-else и имеет следующую форму записи:
if (выражение ) оператор1; else опертор2;
В качестве выполняемого в условном операторе действия может быть другой условный оператор, т.е. допускается использование вложенных операторов if. Оператор if может быть включен в конструкцию if или в конструкцию else.
Оператор if называется вложенным, если хотя бы один из операторов оператор1, оператор2 содержит условные операторы, и используется для программирования вложенных ветвлений.
Ниже на рис. 6.11 приведен пример программирования вложенного ветвления.
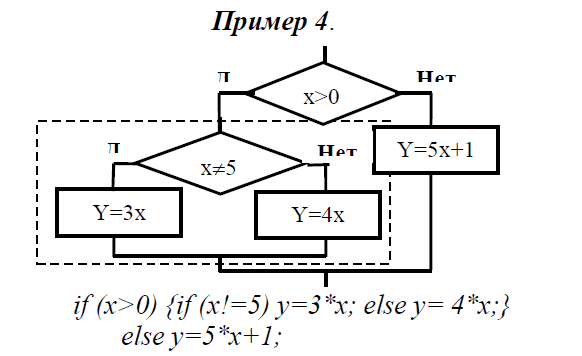
if (x>0) {if (x!=5) y=3*x; else y = 4*x; } else y = 5*x + 1;
Рис. 6.11. Вложенное ветвление
Пример на рис. 6.11 иллюстрирует программирование вложенного ветвления. Фигурные скобки в данном случае не обязательны, так как компилятор относит часть else к ближайшему if.
if ( a<=0)
{y = 5*x + 1; z++;}
else {cout << 'a = "<< a;
if (a>7 && a<>11) y=3*x; else { y = 4*x; z--; }
}
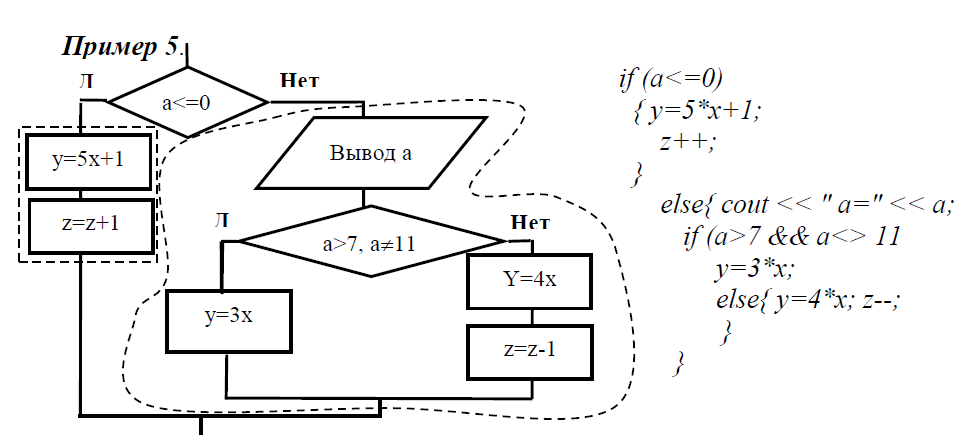
Рис. 6.12. Вложенное ветвление
В примере на рис. 6.12 на ветви "Да" внешнего ветвления имеется группа команд, которой соответствует составной оператор { y=5*x+1; z++;}. На ветви "Нет" этого ветвления имеется группа команд, содержащая другое ветвление. Этой группе команд соответствует составной оператор { cout << " a=" << a; if (a>7 && a<> 11) y=3*x; { y=4*x; z--; } }. Вложенное ветвление на ветви "Да" содержит одну команду (соответствующий оператор y=3*x;), а на ветви "Нет" – две команды, которым соответствует составной оператор { y=4*x; z--; } .
Чтобы сделать программу более читабельной, рекомендуется группировать операторы и конструкции во вложенных операторах if, используя фигурные скобки. Если же фигурные скобки опущены, то компилятор связывает каждое ключевое слово else с наиболее близким if, для которого нет else.
Использование вложенного условного оператора рассмотрим на примерах.
Пример 6.18.
Использование вложенных условных операторов в программах с проверкой многих условий. Примером сложного выбора является оценка знаний ученика по результатам тестирования. Пусть известен результат ЕГЭ (от 0 до 100 баллов). Оценка по пятибалльной шкале должна быть выставлена по правилам:
Оценка = |
|
2, если ЕГЭ <= 40 |
|
3, если 40 < ЕГЭ<=60 |
|
||
4, если 60 < ЕГЭ<=80 |
|
||
5, если 80 < ЕЕЭ<=100. |
|
||
|
|
|
|
В записи этих правил есть избыточность с точки зрения механизмов выполнения условного оператора. Ветвление, это взаимоисключающие варианты, значит, в первой ветви истинность условия ЕГЭ <= 40 означает получение результата. Если же это условие ложно, то к проверке второго условия 40 < ЕГЭ <= 60 приходят только то значения ЕГЭ, которые не удовлетворяют первому условию, то есть только ЕГЭ > 40, а значит, их не нужно включать в запись условия. Так же и в записи всех последующих условий. Логика вложенных операторов условия присоединяет каждый else к ближайшему сверху if.
// Код программы примера 6.18.
#include <stdio.h>
#include <conio.h>
int main ()
{
int Test; // ЕГЭ.
int Ball; // Оценка.
do
{
printf ("Введите результат ЕГЭ испытуемого\n");
scanf ("%d", &Test);
if (Test <= 40)
Ball = 2;
else
if (Test <= 60)
Ball = 3;
else
if (Test <= 80)
Ball = 4;
else
Ball = 5;
printf("Оценка в аттестате: %d\n", Ball);
printf("Если больше нет испытуемых, нажмите ESC\n");
}while (getch() != 27);
} // End of main
Обратите внимание, что цикл по-прежнему управляется событием, но в этом примере вспомогательная переменная key не используется.
Пример 6.19. Вычислить значение функции
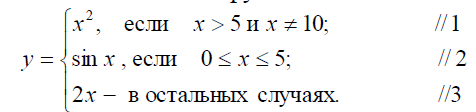
Решение. Необходимо задать значение x и проанализировать, по какой из трех формул, необходимо вычислить y . При этом придется задать один или два вопроса. Например, для x=6, зададим вопрос x>5 и x10? Ответ будет "Да", следовательно, вычислять y надо по первой формуле. Пусть x=3,14159. На вопрос x>5 и x10? ответ будет "Нет", т.е. вычислять y надо по второй или третьей формуле. Для выяснения, по какой конкретно, необходимо задать еще один вопрос, например, 0 x 5? В этом случае ответ будет "Да". Следовательно, y должно вычисляться по второй формуле. Рассуждая аналогично, придем к выводу, что для x=-5 необходимо задать два вопроса x>5 и x10? и 0 x 5? На каждый из вопросов будет получен ответ "Нет", следовательно, y надо вычислять по третьей формуле. Таким образом, приходим к разветвляющемуся алгоритму, изображенному на рис. 6.13. В алгоритме предусмотрен вывод исходных данных, формулы и номера формулы, по которой производится вычисление y.
Сведем в таблицу соответствия (табл. 6.5) обозначения переменных в задаче и в программе.
Таблица 6.5
Таблица соответствия переменных
Обозначения в задаче |
Имена в алгоритме и программе |
Тип данных |
Комментарий |
||
x |
x |
вещественный |
исходное данное – аргумент функции |
||
y |
y |
вещественный |
результат – значение функции |
||
|
n |
целочисленный |
номер формулы |
||
|
z |
строка |
вид формулы |
||
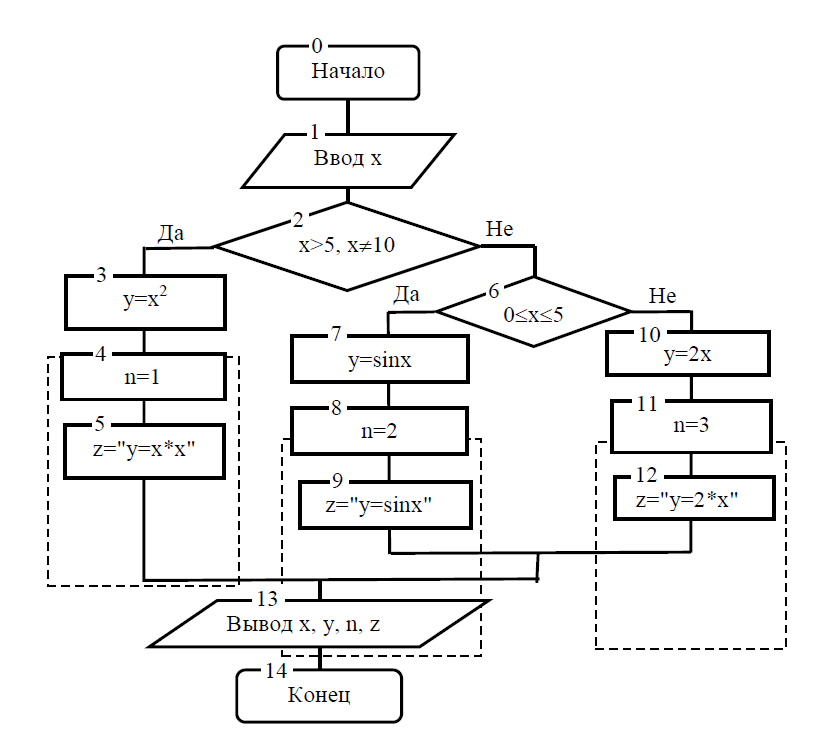
Рис. 6.13. Вложенное ветвление
/* Программа задачи 6.19*/
#include <stdio.h> #include <math.h>
main()
{
float x,y;
int n;
char *z;
puts("Введите x");
scanf("%f",&x);
if(x>5 && x!=10)
{
y=x*x;
n=1;
z="y=x*x";
}
else
if(x>=0 && x<=5)
{
y=sin(x);
n=2;
z="y=sinx";
}
else
{
y=2*x;
n=3;
z="y=2x";
}
printf("При x=%.2f y=%.4f (формула %d:%s)\n",x,y,n,z);
fflush(stdin);
getchar();
return(0);
}
Для проверки правильности разработанного алгоритма и программы достаточно подготовить семь тестов. Сделаем это с помощью рис. 6.14. На рис. 6.14 на числовой оси отмечены промежутки значений x с указанием формул для вычисления y для каждого промежутка и каждой граничной точки. В таблице 9.7 приведены тесты.
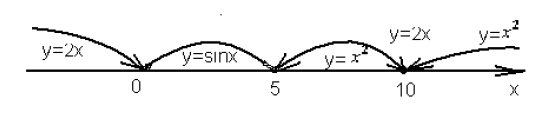
Рисунок 6.14. Промежутки значений x
Таблица 6.6
Тесты к задаче 6.19
Тест № |
Значение x |
Значение y |
Формула для вычисления y |
Тест 1 |
-7.2 |
-14.4 |
y=2x |
Тест 2 |
0 |
0 |
y=sinx |
Тест 3 |
1.5707968 |
1 |
y=sinx |
Тест 4 |
5 |
-0.9589 |
y=sinx |
Тест 5 |
6 |
36 |
y=x2 |
Тест 6 |
10 |
20 |
y=2x |
Тест 7 |
11 |
121 |
y=x2 |
Возможности полной формы условного оператора не ограничиваются только управлением двумя одиночными операторами S1 и S2. Как следует из определения условного оператора, операторы, стоящие в ветвях "Да" и "Нет", могут быть любыми, а значит и условными. Такая структура условного оператора if позволяет описывать разветвляющиеся вычислительные процессы с любым количеством ветвей вычислений. Следовательно, условные операторы могут быть вложены один в другой, то есть либо S1, либо S2, либо оба могут начинаться с if. Например,
А: if (х>у) if (z = w) if (w < p) y = 1; else p=q; else ; else x =4;
C: z =5;
Количество вложений одного условного оператора в другой в языке С++ не ограничивается (в ряде трансляторов с языка С++ число вложений не должно превышать 100).
Пример 6.20. Описать с помощью условного оператора Блок-схему алгоритма, изображенную на рис.6.14.
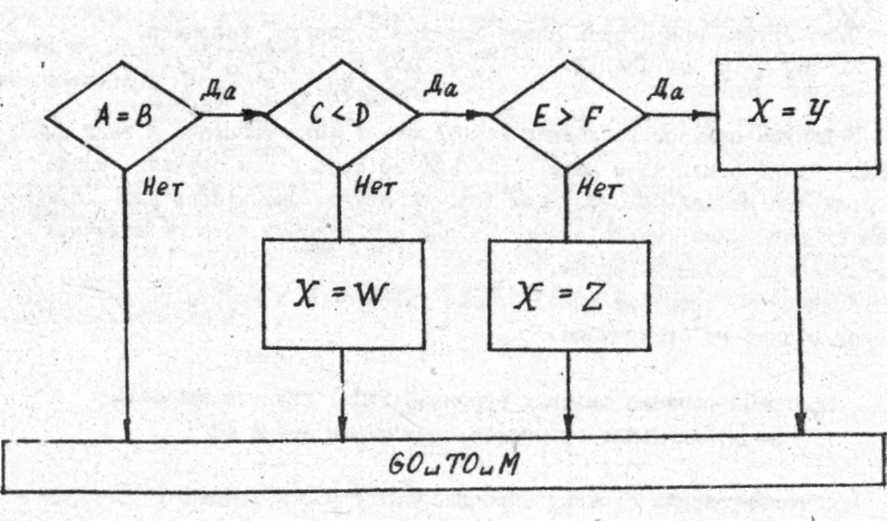
Рис. 6.14. Блок-схема алгоритма примера 6.20
Фрагмент программы на С++, описывающий алгоритм рис. 6.5, может иметь вид
if (a==b) {if (c<d) {if(e>f) x=e; else x=z;} else {x=w; goto FIN;} else goto FIN;
FIN: goto m;
Пример 6.21.
Описать с помощью условного оператора блок-схему алгоритма, изображенную на рис. 6.15.
Фрагмент программы на С++, описывающий алгоритм рис. 6.6, может иметь вид
if (a==b) {if (c<d) {if(e>f) x=y; else goto FIN;} else {x=z; goto FIN;} else {x=w;goto FIN;)
FIN: goto m;
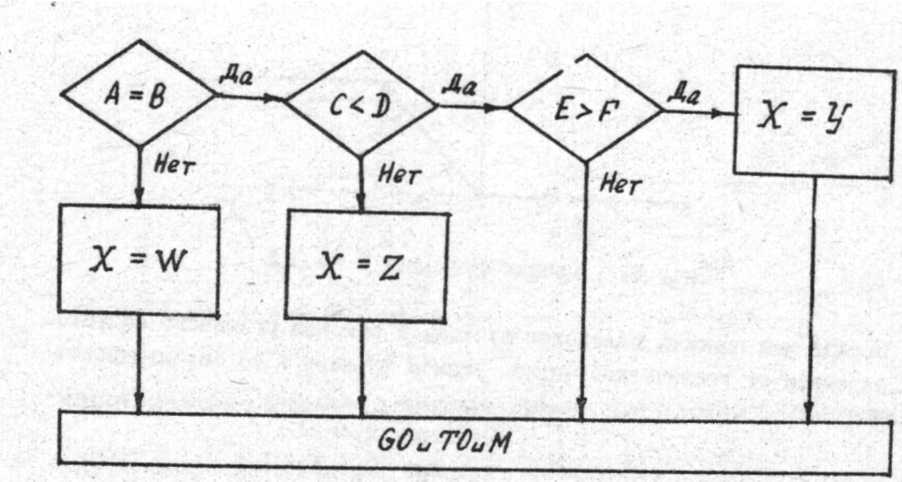
Рис. 6.15. Блок-схема алгоритма примера 6.21
Пример 6.22.
С помощью условного оператора описать поведение функции заданной графически на рис. 6.16.
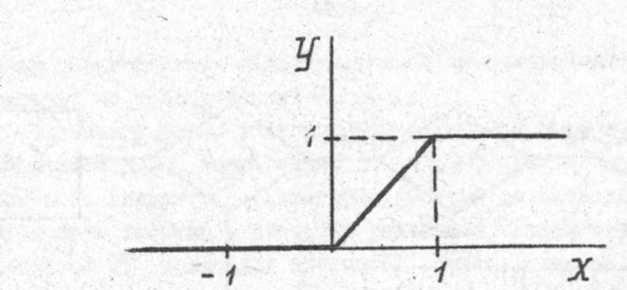
Рис. 6.16. График функции у = f (х)
Прежде чей описать поведение функции с помощью условного оператора, перейдем от графической формы записи функции к ее аналитической записи
0 при х 0;
y = х при 0 < x < 1;
1 при 1.
Обычно аналитическая форма записи поведения функции намного облегчает описание ее поведения средствами языка C++. При аналитической записи таких функций (аналогично приведенной) следует условия поведения функции располагать по нарастанию аргумента или же по убыванию его. Такой порядок записи условий также впоследствии облегчит описание поведения функции средствами языка C++.
Для функции, представленной на рис. 6.16, можно записать несколько вариантов условного оператора:
if (x <= 0) y = 0; else if (x >= 1) y = 1; else y = x;
либо
if (x >= 1) y = 1; else if (x >0) y = x; else y = 0;
В случае использования вложенных условных операторов очень часто в некоторых из них опускается ветвь else . Поэтому, чтобы не было недоразумений в конструкциях условных операторов, во вложенных условных операторах действует следующее правило: ветвь else относится к ближайшему слева if (вернее его ветви "Да"), не имеющей else. Например,
if (a>b) {if (c=d) x = 0; else y = 0;}
Схема выполнения этого оператора представлена на рис. 6.17.
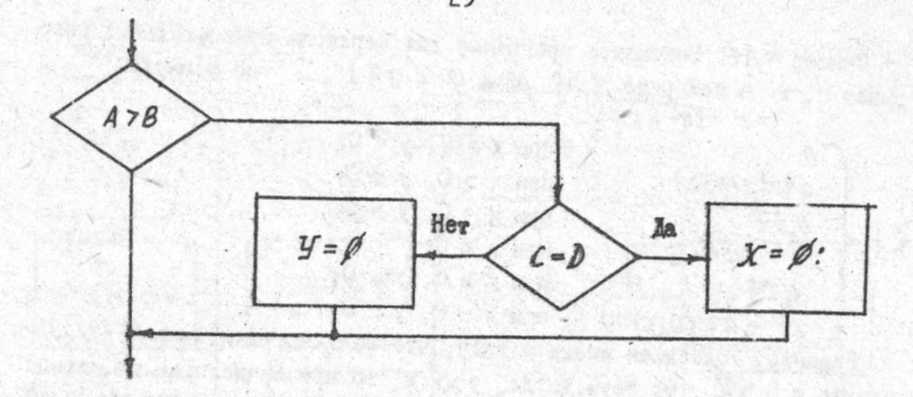
Рис. 6.17. Схема выполнения примера вложенного условного оператора
Лучше всего избегать такого рода конструкций, а если требуется ис-пользовать вложенные операторы if, то либо везде задавать else либо везде опускать.
Пример 6.23
Написать последовательность операторов для вычисления суммы членов ряда
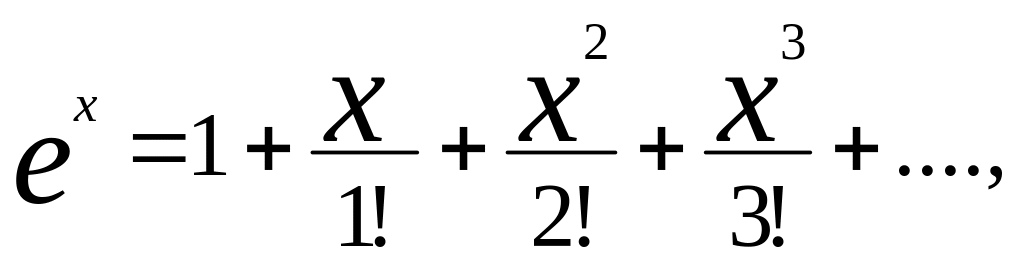
для
которых

Фрагмент программы, реализующей указанные вычисления,может иметь вид
cin >> x;
s = t = 1; n =0;
START: n = n + 1; t = t+x/n;
if fabs(t) > 1e-6 { s = s +t; goto START;}
cout << s << n;
В данном примере с помощью оператора t = t+x/n; реализован итерационный принцип вычисления членов рассматриваемого ряда, то есть каждый последующий член ряда вычисляется путем умножения предыдущего члена ряда на определенный коэффициент.
Рассмотрим примеры составления программ, вычислительные процессы которых реализуются по достаточно сложным разветвляющимся схемам.
Пример 6.24.
Составить программу для перевода прямоугольных координат х, у в полярные r, (0 2) по формулам
|
|
0 |
при х - 0, у - 0; |
|
|
arctan(y/x) |
при х > 0. у а 0; |
|
|
|
0,5 |
при х - 0, у > 0; |
|
|
= |
+ arctan(y/x) |
при х < 0; |
|
|
|
1,5 |
при х - 0, у <. 0; |
|
|
|
2 + arctan(y/x) |
при х > о, у <. 0. |
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Условимся иметь в виду, что если значение |arctan(y/x)| близко к 0,5, то есть, когда у >> х, то при вычислении на машине возможен аварийный останов. Поэтому при у > х следует arctan(y/x) вычислять через дополнительный угол arctan(x/y). Обозначим: p = arctan(y/x), q = arctan(x/y).
Блок-схема алгоритма решения задачи приведена на рис. 6.18.
Таблица 6.7
Таблица идентификаторов примера 6.16
В исходном выражении |
x |
y |
r |
|
|
p |
q |
| | |
|
sign |
m1 |
arctg |
В программе на языке С++ |
x |
y |
r |
fi |
pi |
p |
q |
fabs |
sqrt |
sign |
m1 |
atan |
Учитывая сделанные замечания, программу можно записать в следующеем виде:
#include <stdio.h>
#include <math.h>
int main ()
{
float x, y, r, fi, pi, p, q;
cout << "Ввведите х и у:"
cin >> x >> y;
pi = 3.1415926;
r = sqrt (x*x + y*y);
if (x= 0) {if (y=0) fi=0; else {if (y>0) fi=pi/2; else fi =3*pi/2;
goto M1;
}
else
{if (fabs(x)>=fabs(y)) p = atn(y/x); else { q = atan(x/y); p = (pi/2 – fabs(q))*sign(q);}
if (x<0) fi = pi +p; else if (y>=0) fi = p; else fi = 2*pi + p;
}
M1: cout << "r = " << r "fi = " << fi << endl;
getch();
return 0;
}
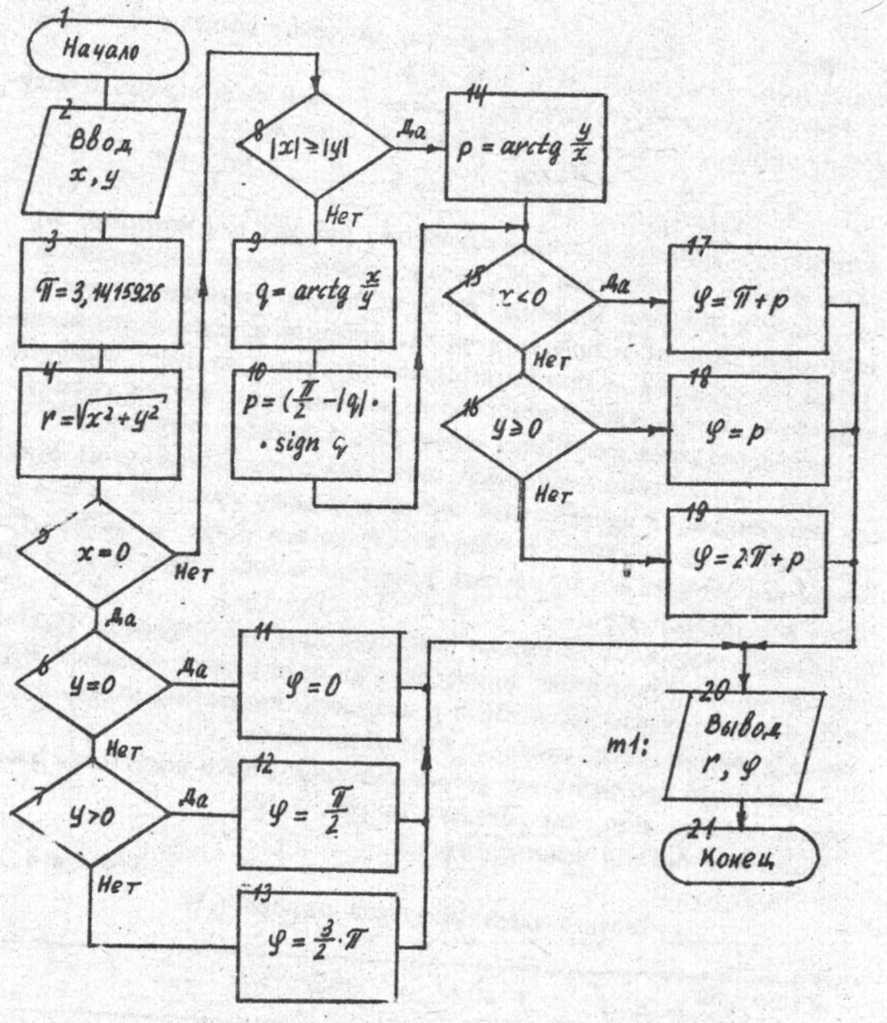
Рис. 6.18. Блок-схема алгоритма примера 6.24
Пример 6.25
Классической задачей, рассматриваемой в большинстве учебников по программированию, является определение корней квадратного уравнения вида ax2 + bx + c = 0.
Решение. Существуют различные методы решения этой задачи. В частности, можно воспользоваться привычными формулами;
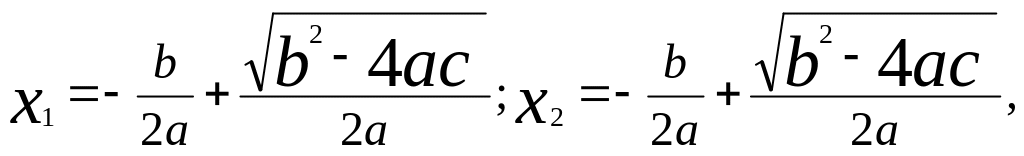
которые будут лежать в основе алгоритма, так как они указывают последовательность действий при решении задачи. После подстановки в эти формулы числовых значений а, в, c производятся вычисления, и получается решение в виде двух чисел. Остается предусмотреть исключительные ситуации, в противном случае программа не будет полностью описывать вычислительный процесс, то есть не будет универсальной. Исключительными ситуациями могут быть следующие ситуации:
1) а = 0. Уравнение перестает быть квадратным. Приведенные формулы неприемлемы, и единственный корень линейного уравнения вх + с = 0 вычисляется по формуле: х = - с/в. Случай в = 0 при а = 0 требует, чтобы при этом и с = 0, то есть уравнение вообще отсутствует и задачи как таковой нет.
2) в2 - 4ас 0. В случае равенства нулю дискриминанта уравнение имеет два совпадающих корня; если же подкоренное выражение отрицательное, то корни комплексные и вычислять квадратный корень следует из значения этого выражения с обратным знаком.
Этапы решения:
1. Анализ условия задачи. Квадратное уравнение может иметь одно или два решения, или не иметь их вообще. Результат решения зависит от определителя уравнения, вычисляемого по формуле d = b2 – 4ac.
2. Входными данными являются коэффициенты уравнения a, b, c. Чтобы уравнение осталось квадратным, первый коэффициент должен быть отличен от нуля. Имена переменных, обозначающих коэффициенты, могут совпадать с их математической записью, то есть a, b, c. Тип коэффициентов вещественный.
3. Выходными данными программы будут значения корней уравнения, если их удастся найти по формулам
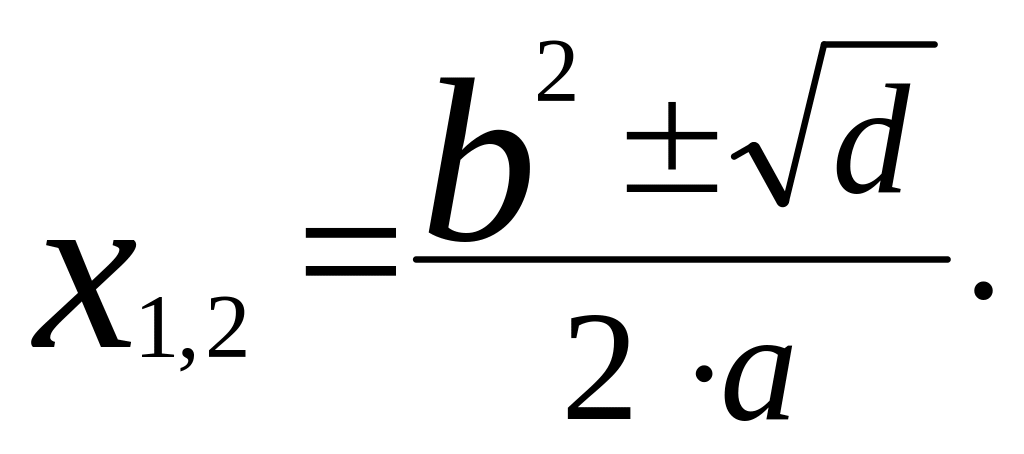
Если же корней нет, об этом следует напечатать сообщение.
4. Для вычисления и хранения значения определителя требуется ввести новую переменную, которая не является результатом задачи, но необходима для ее решения. Такие переменные называются рабочими переменными программы. Обозначим ее буквой d, как и в постановке задачи.
5. Определение необходимых формул вычисления очевидно.
6. Кодирование алгоритма. При выполнении алгоритма можно выполнить предварительное словесное описание:
1) ввести значения коэффициентов (названы a, b ,c);
2) вычислить дискриминант (назван d);
3) если дискриминант отрицательный, решения нет, вывести сообщение;
4) если дискриминант > или = 0, решение есть, вычислить значения корней и вывести на печать.
Рассмотрим использование составных операторов при решении этой задачи.
В первой ветви условного оператора нужно выполнить не одно, а три действия, поэтому используется блок {…}, который показывает компилятору, что эти действия следует воспринимать как единое целое.
Блок-схема программы для рассматриваемой задачи может быть изображена в таком виде, как показано на рис. 6.19.
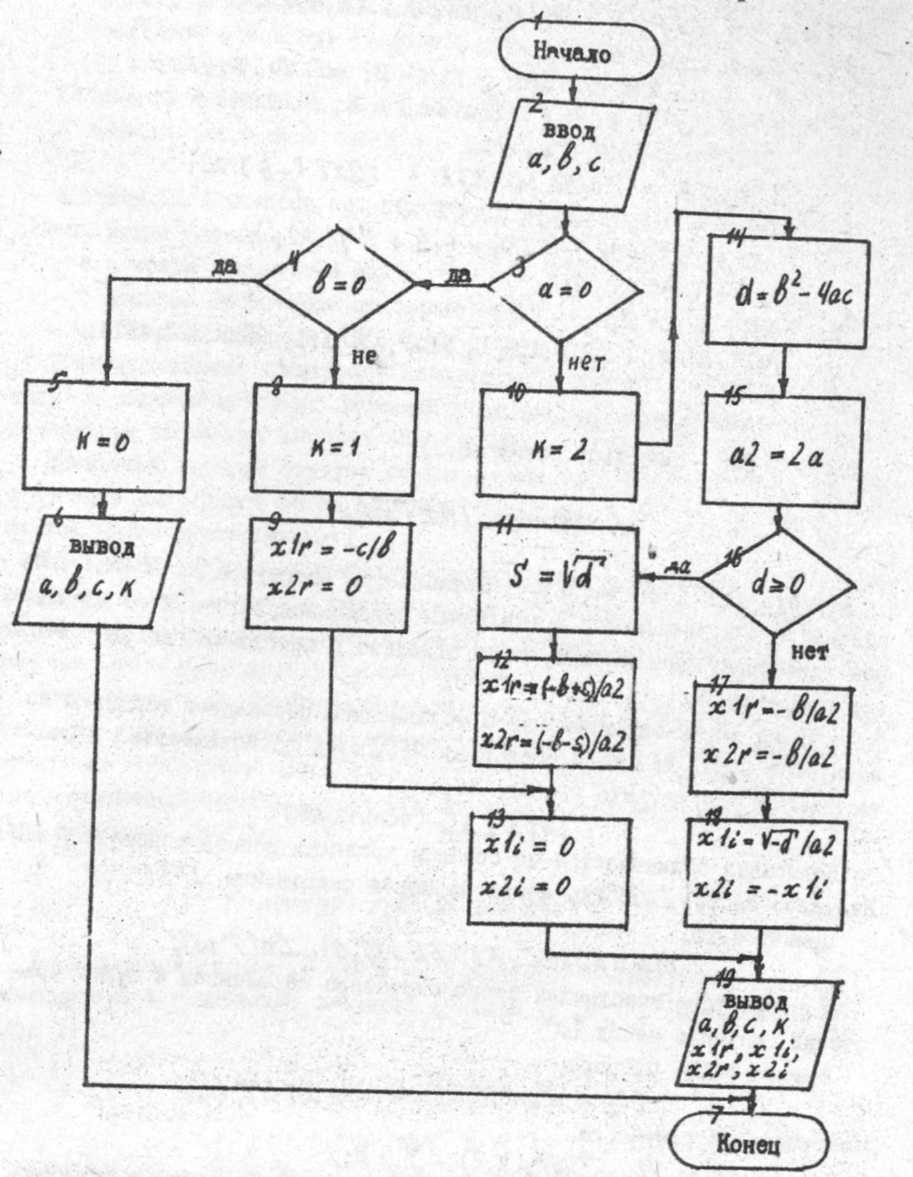
Рис. 6.19. Блок-схема алгоритма решения квадратного уравнения
Составим таблицу идентификаторов.
Таблица 6.8
Таблица идентификаторов примера 6.25
В исходном выражении |
a |
b |
c |
k |
d |
A2 |
X1r |
X2r |
X1i |
X2i |
s |
|
В программе на С++ |
|
|
|
|
|
|
|
|
|
|
|
sqrt |
Программа решения квадратного уравнения, составленная в соответствии с блок-схемой, приведенной на рис. 6.19, будет иметь следующий вид:
// Код программы примера 6.25
#include <stdio.h>
#include <math.h>
int main ()
{
float a, b, c, d;
float x1, x2;
// Ввод входных данных
cout << "\nВведите коэффициенты квадратного уравнения:\n";
cout << "a = " ; cin >> a;
cout << "b = " ; cin >> b;
cout << "c = " ; cin >> c;
cout << "\nБыли введены коэффициенты квадратного уравнения:\n";
cout << "a = " << a << " b = " << b << " c = " << c << endl;
d = b*b – 4*a*c; //Вычисление дискриминанта d.
if (d >= 0.0)
{
x1 = ( – b + sqrt(d)) / (2.*a); //Вычисление корней.
x2 = ( – b – sqrt(d)) / (2.*a);
cout << " Корни равны: ";
cout << " x1 = " ; cin >> x1; cout << " x2 = " ; cin >> x2;
}
else
cout <<"Корней нет\n"; //Печать сообщения.
} // End of main
В этом примере не предусмотрен случай равных корней, например, при a=2, b=4, c=2. Для того чтобы отследить этот случай, потребуется внести изменение в текст программы.
Пример 6.26. Когда для принятия решения требуется проверка более одного условия, появляется множественное ветвление. В данном примере следует предусмотреть случай равных корней, при этом в условном операторе появляется второе условие: d = 0, а значит, и второй оператор проверки условия.
Схема алгоритма условно может быть изображена так:
if (d > 0)
{
// Блок операторов, чтобы вычислить два корня.
}
else
if (d = = 0)
{
//Блок операторов, чтобы вычислить один корень.
}
else
{
//Вывод сообщения о том, что решения нет.
}
Структура ветвления рассматривает только взаимоисключающие варианты. Выполнение оператора if при использовании многих условий, если они не выделены блоком, разворачивается по принципу матрешки, то есть каждый else принадлежит ближайшему сверху if. Отступы в тексте программы позволяют лучше увидеть логику выбора решения.
// Код программы примера 6.26
#include <stdio.h>
#include <math.h>
int main (vid)
{
float a, b, c, d;
float x1, x2;
cout << "\nВведите коэффициенты квадратного уравнения:\n";
cout << "a = " ; cin >> a;
cout << "b = " ; cin >> b;
cout << "c = " ; cin >> c;
cout << "\nБыли введены коэффициенты квадратного уравнения:\n";
cout << "a = " << a << " b = " << b << " c = " << c << endl;
d = b*b – 4*a*c;
if (d >0.0)
{
x1 = ( – b + sqrt (d)) / (2.*a);
x2 = ( – b – sqrt (d)) / (2.*a);
cout << " Корни равны: ";
cout << " x1 = " ; cin >> x1; cout << " x2 = " ; cin >> x2;
}
else
// Дискриминант d вещественное значение, сравнивать его с нулем можно только
// с некоторой степенью точности, например, так: |d|<0.00001.
if ( fabs (d) <= 0.00001) // Приблизительно равен нулю.
{
x1 = ( – b + sqrt (d)) / (2.*a);
cout << " Корни одинаковы: ";
cout << " x1 = " ; cin >> x1;
}
else
cout << "Корней нет\n";
} // End of main
Пример 6.27. Диалог с программой в общепринятом виде. Для полного тестирования программы, алгоритм которой проверяет множество условий, нужно выполнить столько примеров, сколько вариантов ветвления возможно. В программе примера 6.27 нужно выполнить три тестовых примера. Кроме того, пользователь с помощью программы может решать несколько уравнений. Поэтому необходимо уметь организовать многократное обращение к программе.
Для организации повторного выполнения программы или ее фрагмента используется циклический алгоритм. Этот цикл будет управляться внешним событием. Событие порождает пользователь, нажимая клавишу на клавиатуре. Общепринято использовать клавишу Esc для завершения процесса, а для продолжения клавишу Enter или любую другую.
Кроме того, при вводе данных необходимо предусмотреть, чтобы введенное значение коэффициента а было бы отлично от 0. Проверка выполняется в цикле сразу же после ввода данных. Цикл будет повторен всегда, когда введенное значение не соответствует правилам, и только при правильных данных программа продолжит работу.
// Код программы примера 6.27.
//Показывает пример диалога в общепринятом виде.
// Для управления используется оператор do…while
//с выходом по условию
// «нажата клавиша Esc».
#include <stdio.h>
#include <math.h>
#include <conio.h> // Библиотека консольного ввода-вывода.
#define ESC 27 // Код клавиши Esc в символьном представлении.
int main ()
{
float a, b, c, d;
float x1, x2;
char key; // Переменная key для обработки события.
// Первое выполнение алгоритма обязательно, поэтому необходим цикл do...while
do
{
// Проверка корректности вводимых данных.
// Если введенное значение а близко к нулю, цикл ввода повторяется.
do
{
cout << "\nВведите коэффициенты квадратного уравнения:\n";
cout << "a = " ; cin >> a;
cout << "b = " ; cin >> b;
cout << "c = " ; cin >> c;
cout << "\nБыли введены коэффициенты квадратного уравнения:\n";
cout << "a = " << a << " b = " << b << " c = " << c << endl;
} while (fabs (a) < 0.001)
// Ввод выполнен правильно.
d = b*b – 4*a*c;
if (fabs (d) <= 0.00001)
{
x1 = ( – b + sqrt (d)) / (2.*a);
cout << " Корни одинаковы: x1 = x2 = "; cin >> x1;
}
else
if ( d > 0)
{
x1 = ( – b + sqrt (d)) / (2.*a);
x2 = ( – b – sqrt (d)) / (2.*a);
cout << " Корни равны: ";
cout << " x1 = " ; cin >> x1; cout << " x2 = " ; cin >> x2;
}
else
cout << "Корней нет\n";
// Обработка события «нажатие клавиши».
printf ("Клавиша ESC – завершение работы, Any Key – продолжение...");
// Ожидание события «нажатие клавиши».
key = getch (); // Функция getch () читает символьный код клавиши.
} while ( key != ESC ) // Код клавиши Esc прописан в директиве define.
} // End of main
Запомните:
Перед закрывающей фигурной скобкой точку с запятой ставить обязательно, а после скобки точка с запятой не ставится.