
Алгоритм нахождения ранга матрицы.
Пусть требуется
вычислить ранг матрицы
размеров
.
Если матрица
нулевая,
то по определению
![]() .
В противном случае с помощью перестановки
строк и столбцов матрицы добиваемся
того, чтобы в левом верхнем углу матрицы
стоял ненулевой элемент. Итак, считаем,
что
.
В противном случае с помощью перестановки
строк и столбцов матрицы добиваемся
того, чтобы в левом верхнем углу матрицы
стоял ненулевой элемент. Итак, считаем,
что
![]() .
.
Первую строку
оставляем без изменений. Ко второй
строке прибавляем первую, умноженную
на число
 .
В результате вторая строка принимает
вид
.
В результате вторая строка принимает
вид
![]()
Затем к третьей
строке прибавляем первую строку,
умноженную на число
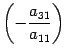 .
В результате третья строка принимает
вид
.
В результате третья строка принимает
вид
![]()
Процесс продолжаем до тех пор, пока не получим нуль на первом месте в последней строке.
Преобразованная матрица имеет вид
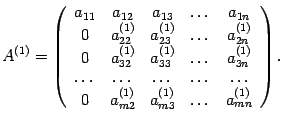
Если все строки,
начиная со второй, в полученной матрице
нулевые, то ее ранг равен 1, так как есть
минор первого порядка, отличный от нуля
![]() .
В противном случае перестановкой строк
и столбцов матрицы с номерами, большими
единицы, добиваемся, чтобы второй элемент
второй строки был отличен от нуля. Итак,
считаем, что
.
В противном случае перестановкой строк
и столбцов матрицы с номерами, большими
единицы, добиваемся, чтобы второй элемент
второй строки был отличен от нуля. Итак,
считаем, что
![]() .
.
Первую и вторую
строки оставляем без изменений. К третьей
строке прибавляем вторую, умноженную
на число
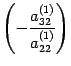 .
В результате получим, что второй элемент
третьей строки равен нулю. Затем к
четвертой строке прибавляем вторую,
умноженную на число
.
В результате получим, что второй элемент
третьей строки равен нулю. Затем к
четвертой строке прибавляем вторую,
умноженную на число
 ,
и т.д. В результате получаем матрицу
,
и т.д. В результате получаем матрицу

Если все строки,
начиная с третьей, нулевые, то
![]() ,
так как минор
,
так как минор
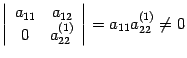 .
В противном случае перестановкой строк
и столбцов с номерами, большими двух,
добиваемся, чтобы третий элемент третьей
строки был отличен от нуля. Далее,
добавлением третьей строки, умноженной
на соответствующие числа, к строкам с
большими номерами получаем нули в
третьем столбце, начиная с четвертого
элемента, и т.д.
.
В противном случае перестановкой строк
и столбцов с номерами, большими двух,
добиваемся, чтобы третий элемент третьей
строки был отличен от нуля. Далее,
добавлением третьей строки, умноженной
на соответствующие числа, к строкам с
большими номерами получаем нули в
третьем столбце, начиная с четвертого
элемента, и т.д.
На каком-то этапе
мы придем к матрице, у которой все строки,
начиная с
![]() -ой
, равны нулю (или отсутствуют при
-ой
, равны нулю (или отсутствуют при
![]() ),
а минор в первых
строках
и первых
столбцах
является определителем треугольной
матрицы с ненулевыми элементами на
диагонали. Ранг такой матрицы равен
.
Следовательно,
),
а минор в первых
строках
и первых
столбцах
является определителем треугольной
матрицы с ненулевыми элементами на
диагонали. Ранг такой матрицы равен
.
Следовательно,
![]() .
.
Замечание 14.15 В предложенном алгоритме нахождения ранга матрицы все вычисления должны производиться без округлений. Сколь угодно малое изменение хотя бы в одном из элементов промежуточных матриц может привести к тому, что полученный ответ будет отличаться от ранга исходной матрицы на несколько единиц.
Замечание 14.16 Если в исходной матрице элементы были целыми числами, то и вычисления удобно производить без использования дробей. Поэтому на каждом этапе целесообразно умножать строки на такие числа, чтобы при вычислениях дроби не возникали.
Пример 14.12
Найдите ранг матрицы
 .
.
Решение. Первую строку оставляем без изменений. Чтобы избежать появления дробей, умножим вторую, третью и четвертую строки на 2:
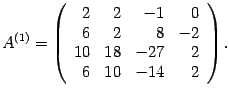
Первую строку
умножим на
![]() и
прибавим ко второй. Получим строку
и
прибавим ко второй. Получим строку
![]() .
Первую строку умножим на
.
Первую строку умножим на
![]() и
прибавим к третьей. Получим строку
и
прибавим к третьей. Получим строку
![]() .
Первую строку умножим на
и
прибавим к четвертой. Получим строку
.
Первую строку умножим на
и
прибавим к четвертой. Получим строку
![]() .
В итоге имеем матрицу
.
В итоге имеем матрицу

Вторую строку
оставляем без изменений. К третьей
строке прибавляем вторую, умноженную
на 2. Получим строку
![]() .
К четвертой строке прибавляем вторую.
Получим нулевую строку. Преобразованная
матрица имеет вид
.
К четвертой строке прибавляем вторую.
Получим нулевую строку. Преобразованная
матрица имеет вид
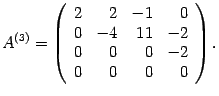
Поменяем местами третий и четвертый столбцы:

Базисный минор
матрицы
![]() стоит
в первых трех столбцах и первых трех
строках,
стоит
в первых трех столбцах и первых трех
строках,
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Замечание 14.17 В приведенном примере вычисления были бы проще, если сначала четвертый столбец сделать первым и четвертую строку сделать первой. Но для того, чтобы догадаться об этом, нужно анализировать вопросы делимости чисел, что достаточно сложно описать в алгоритме, пригодном для всех случаев.
![]()
